3.3 二元一次方程组及其解法 第1课时课件(共14张PPT) 沪科版七年级数学上册
文档属性
| 名称 | 3.3 二元一次方程组及其解法 第1课时课件(共14张PPT) 沪科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 01:04:05 | ||
图片预览






文档简介
(共14张PPT)
3.3 二元一次方程组及其解法 第1课时
第3章 一次方程与方程组
1.理解二元一次方程(组)的概念,能判别二元一次方程(组);
2.能根据实际问题中的等量关系列出二元一次方程组.
活动1:看图写出其中的等量关系.
任务一:会辨别二元一次方程(组)
问题1:若要求它们各驮了多少包裹,有哪几个未知数?
问题2:列出一元一次方程.
这么大的个,才比我多驮了2个.
哼,我从你背上拿来1个,我的包裹数就是你的2倍!
老黑 小灰
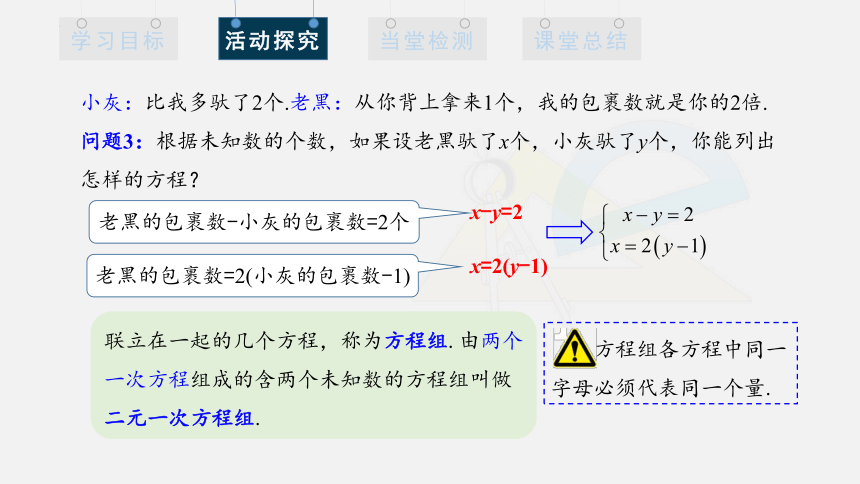
小灰:比我多驮了2个.老黑:从你背上拿来1个,我的包裹数就是你的2倍.
问题3:根据未知数的个数,如果设老黑驮了x个,小灰驮了y个,你能列出怎样的方程?
x-y=2
老黑的包裹数-小灰的包裹数=2个
老黑的包裹数=2(小灰的包裹数-1)
x=2(y-1)
观察:比较这两个方程与我们所学过的一元一次方程有何不同?
尝试说一说什么是二元一次方程.
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
小灰:比我多驮了2个.老黑:从你背上拿来1个,我的包裹数就是你的2倍.
问题3:根据未知数的个数,如果设老黑驮了x个,小灰驮了y个,你能列出怎样的方程?
x-y=2
老黑的包裹数-小灰的包裹数=2个
老黑的包裹数=2(小灰的包裹数-1)
x=2(y-1)
联立在一起的几个方程,称为方程组.由两个一次方程组成的含两个未知数的方程组叫做二元一次方程组.
方程组各方程中同一字母必须代表同一个量.
活动2:根据二元一次方程(组)的概念,完成下列两个关卡.
关卡1:已知|m-1|x|m|+y2n-1=3是二元一次方程,求m+n的值.
关卡2:下列方程组是二元一次方程组吗?为什么?
解:根据题意得|m-1|≠0,
且|m|=1,2n-1=1,
解得:m=-1,n=1,
所以m+n=0.
方程组 是关于x、y的二元一次方程组,
则ab的值是 .
练一练
-1
活动:分析下列情境列出相应方程组,和同伴交流答案.
情境1:买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元,乙种水的桶数是甲种水的桶数的75%,问:甲种、乙种水各多少桶?
情境2:加工某种产品须经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序.应怎样安排人力,才能使每天第一、二道工序所完成的件数相等.
任务二:能根据实际情况列二元一次方程组
情境1:买甲、乙种水用250元,甲种水每桶8元,乙种水每桶6元,乙种水的桶数是甲种水的桶数的75%.
情境2:第一道工序每人每天可完成900件,第二道工序1200件.7位工人,每天第一、二道工序所完成的件数相等.
解:设安排x人去第一道工序,y人去第二道,根据题意得 .
解:设甲种水x桶,乙种y桶,根据题意得 .
小组讨论:根据问题列二元一次方程组的步骤有哪些?
列二元一次方程组的一般步骤:
①审:弄清题意和题目中的数量关系;
②设:用字母表示题目中的两个未知数;
③找:找出能够表示应用题全部含义的一个相等关系;
④列:根据这个相等关系列出重要的代数式,从而列出方程.
1.下列哪些方程是二元一次方程?如不是,说明理由.
(1) +2y=1;(2)x+ = -7 ;
(3)2x2-x+1=0 ;(4)2(x+y)-3(x-y)=1;(5)2x+5=10.
解:(1)是;
(2)不是,y出现在分母中;
(3)不是,x的最高次数是2,不是1;
(4)是;
(5)不是,是一元一次方程.
2.已知方程2xm+2+3y2n=17是一个二元一次方程,则m= ,n= .
3.已知方程组 是二元一次方程组,则m的值是 .
-1
0.5
1
4.某班学生39人,到公园划船,共租用9艘船,每艘大船可坐5人,每艘小船可坐3人,每艘船都坐满.问:大船、小船各租了多少艘?(只列方程组即可)
解:设大船租了x艘,小船租了y艘,
根据题意得 .
回顾本节课,说一说你都学到了哪些知识?
二元一次方程
根据实际问题列二元一次方程组
二元一次方程组
概 念
3.3 二元一次方程组及其解法 第1课时
第3章 一次方程与方程组
1.理解二元一次方程(组)的概念,能判别二元一次方程(组);
2.能根据实际问题中的等量关系列出二元一次方程组.
活动1:看图写出其中的等量关系.
任务一:会辨别二元一次方程(组)
问题1:若要求它们各驮了多少包裹,有哪几个未知数?
问题2:列出一元一次方程.
这么大的个,才比我多驮了2个.
哼,我从你背上拿来1个,我的包裹数就是你的2倍!
老黑 小灰
小灰:比我多驮了2个.老黑:从你背上拿来1个,我的包裹数就是你的2倍.
问题3:根据未知数的个数,如果设老黑驮了x个,小灰驮了y个,你能列出怎样的方程?
x-y=2
老黑的包裹数-小灰的包裹数=2个
老黑的包裹数=2(小灰的包裹数-1)
x=2(y-1)
观察:比较这两个方程与我们所学过的一元一次方程有何不同?
尝试说一说什么是二元一次方程.
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
小灰:比我多驮了2个.老黑:从你背上拿来1个,我的包裹数就是你的2倍.
问题3:根据未知数的个数,如果设老黑驮了x个,小灰驮了y个,你能列出怎样的方程?
x-y=2
老黑的包裹数-小灰的包裹数=2个
老黑的包裹数=2(小灰的包裹数-1)
x=2(y-1)
联立在一起的几个方程,称为方程组.由两个一次方程组成的含两个未知数的方程组叫做二元一次方程组.
方程组各方程中同一字母必须代表同一个量.
活动2:根据二元一次方程(组)的概念,完成下列两个关卡.
关卡1:已知|m-1|x|m|+y2n-1=3是二元一次方程,求m+n的值.
关卡2:下列方程组是二元一次方程组吗?为什么?
解:根据题意得|m-1|≠0,
且|m|=1,2n-1=1,
解得:m=-1,n=1,
所以m+n=0.
方程组 是关于x、y的二元一次方程组,
则ab的值是 .
练一练
-1
活动:分析下列情境列出相应方程组,和同伴交流答案.
情境1:买甲、乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元,乙种水的桶数是甲种水的桶数的75%,问:甲种、乙种水各多少桶?
情境2:加工某种产品须经两道工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1200件.现有7位工人参加这两道工序.应怎样安排人力,才能使每天第一、二道工序所完成的件数相等.
任务二:能根据实际情况列二元一次方程组
情境1:买甲、乙种水用250元,甲种水每桶8元,乙种水每桶6元,乙种水的桶数是甲种水的桶数的75%.
情境2:第一道工序每人每天可完成900件,第二道工序1200件.7位工人,每天第一、二道工序所完成的件数相等.
解:设安排x人去第一道工序,y人去第二道,根据题意得 .
解:设甲种水x桶,乙种y桶,根据题意得 .
小组讨论:根据问题列二元一次方程组的步骤有哪些?
列二元一次方程组的一般步骤:
①审:弄清题意和题目中的数量关系;
②设:用字母表示题目中的两个未知数;
③找:找出能够表示应用题全部含义的一个相等关系;
④列:根据这个相等关系列出重要的代数式,从而列出方程.
1.下列哪些方程是二元一次方程?如不是,说明理由.
(1) +2y=1;(2)x+ = -7 ;
(3)2x2-x+1=0 ;(4)2(x+y)-3(x-y)=1;(5)2x+5=10.
解:(1)是;
(2)不是,y出现在分母中;
(3)不是,x的最高次数是2,不是1;
(4)是;
(5)不是,是一元一次方程.
2.已知方程2xm+2+3y2n=17是一个二元一次方程,则m= ,n= .
3.已知方程组 是二元一次方程组,则m的值是 .
-1
0.5
1
4.某班学生39人,到公园划船,共租用9艘船,每艘大船可坐5人,每艘小船可坐3人,每艘船都坐满.问:大船、小船各租了多少艘?(只列方程组即可)
解:设大船租了x艘,小船租了y艘,
根据题意得 .
回顾本节课,说一说你都学到了哪些知识?
二元一次方程
根据实际问题列二元一次方程组
二元一次方程组
概 念
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
