13.1平方根(3)
图片预览




文档简介
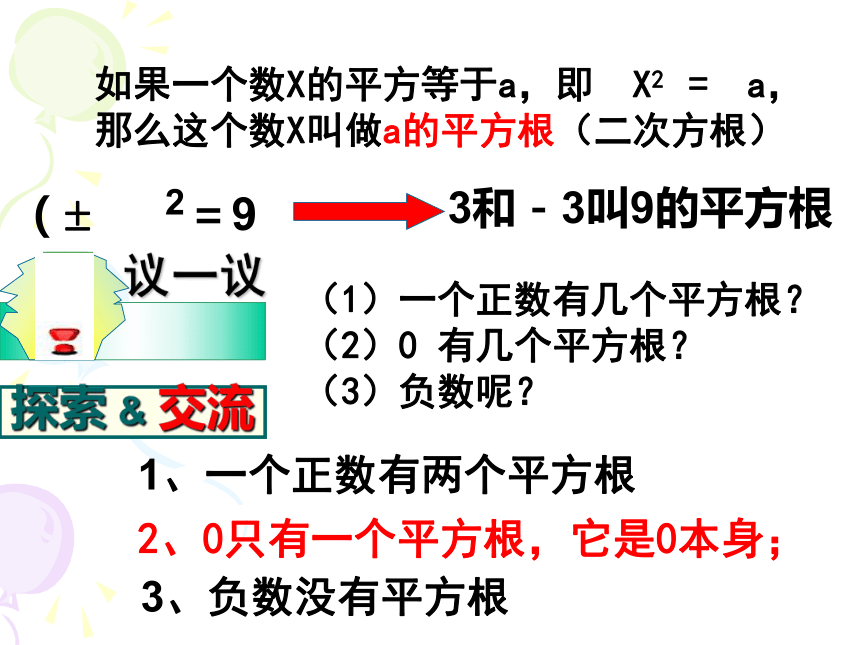
课件14张PPT。13.1.2平方根±0.8±3±4±1±6±7 如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?探索 & 交流1、一个正数有两个平方根2、0只有一个平方根,它是0本身;3、负数没有平方根如果一个数X的平方等于a,即 X2 = a,
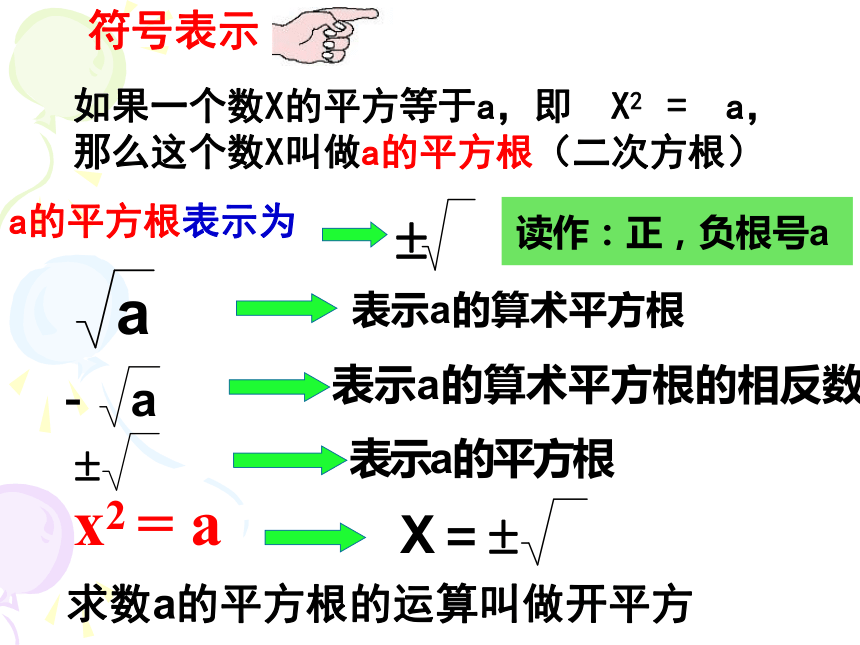
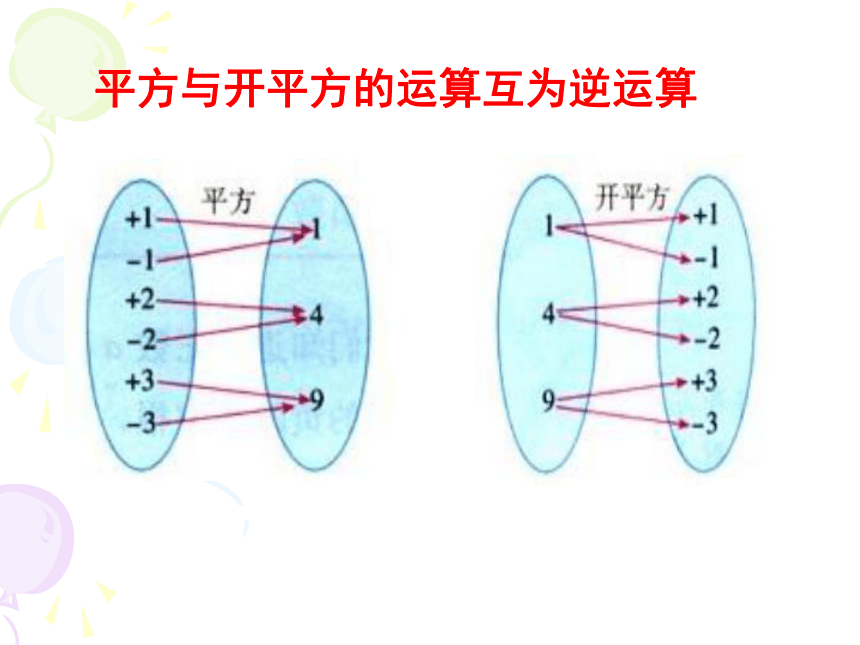
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方 平方与开平方的运算互为逆运算例1 求下列各数的平方根:(1) 100;(3) 0.25(4) (-2005)2(5)11(5)11的平方根是解: (1)∵(±10)2=100,∴100的平方根是±10, (3)∵(±0.5)2=0.25,
∴0.25的平方根是±0.5, (4)∵(±2005)2=(-2005)2,
∴(-2005)2的平方根是±2005,即例2 求下列各式的值:
(3)解11-110.6-0.6P16764解解:面积为A的正方形的边长为P1674、填空±5550.6-11思考: 你能求出下列各式中的未知数x吗?
(1) 3x2-6.75=0(2)(x-1)2=4解: (1) x2=2.25
(2) x-1=±2
(3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 同步P981、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?go作业作业本
那么这个数X叫做a的平方根(二次方根)(1)一个正数有几个平方根?
(2)0 有几个平方根?
(3)负数呢?探索 & 交流1、一个正数有两个平方根2、0只有一个平方根,它是0本身;3、负数没有平方根如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a符号表示求数a的平方根的运算叫做开平方 平方与开平方的运算互为逆运算例1 求下列各数的平方根:(1) 100;(3) 0.25(4) (-2005)2(5)11(5)11的平方根是解: (1)∵(±10)2=100,∴100的平方根是±10, (3)∵(±0.5)2=0.25,
∴0.25的平方根是±0.5, (4)∵(±2005)2=(-2005)2,
∴(-2005)2的平方根是±2005,即例2 求下列各式的值:
(3)解11-110.6-0.6P16764解解:面积为A的正方形的边长为P1674、填空±5550.6-11思考: 你能求出下列各式中的未知数x吗?
(1) 3x2-6.75=0(2)(x-1)2=4解: (1) x2=2.25
(2) x-1=±2
(3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 同步P981、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?go作业作业本
