人教中图版(2019)必修1 高中信息技术 第2章 算法与程序实现 测试卷(word版,含答案)
文档属性
| 名称 | 人教中图版(2019)必修1 高中信息技术 第2章 算法与程序实现 测试卷(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 590.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教中图版(2019) | ||
| 科目 | 信息科技(信息技术) | ||
| 更新时间 | 2023-12-16 22:43:16 | ||
图片预览

文档简介
第二章 算法与程序实现 测试卷
一、选择题
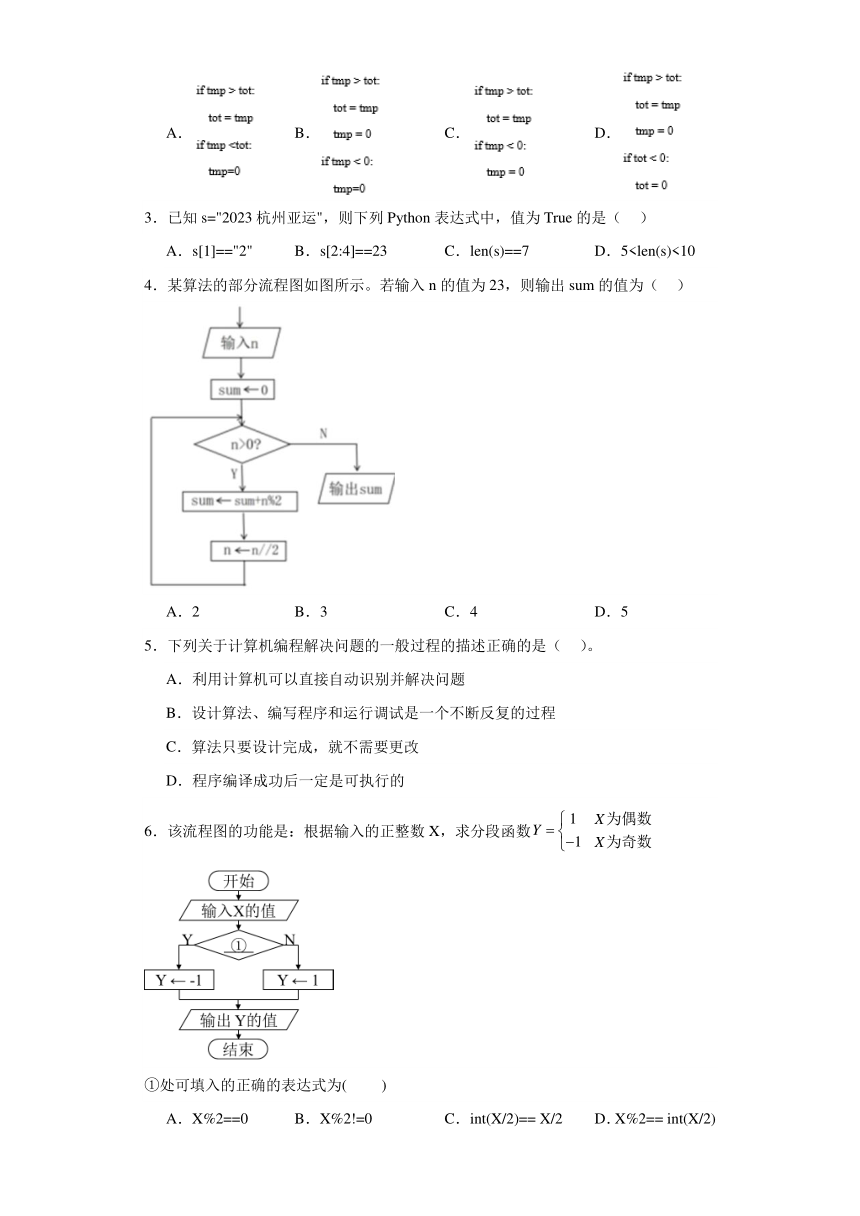
1.某算法的部分流程图如图所示,以下说法正确的是( )
A.若输入n的值为1,则无法输出“验证成功”的结果
B.该算法只有在输入n的值是偶数时,才能执行成功
C.若输入n的值为2,则“n≠1”的判断次数为1次
D.若输入n的值为5,则“n是偶数 ”的判断次数为5次
2.子序列是指数组中连续的若干个元素(至少1个元素)。数组a中有n个整型元素(有正有负),现要查找和最大的子序列,并输出和。实现该功能的程序段如下,方框中应填入的正确代码为( )
def maxsub(a):
tot=-1; tmp = 0
for num in a:
tmp += num
return tot
a = [-2,1,-3,4,-1,2,1,-5,4]
print(maxsub(a))
A. B. C. D.
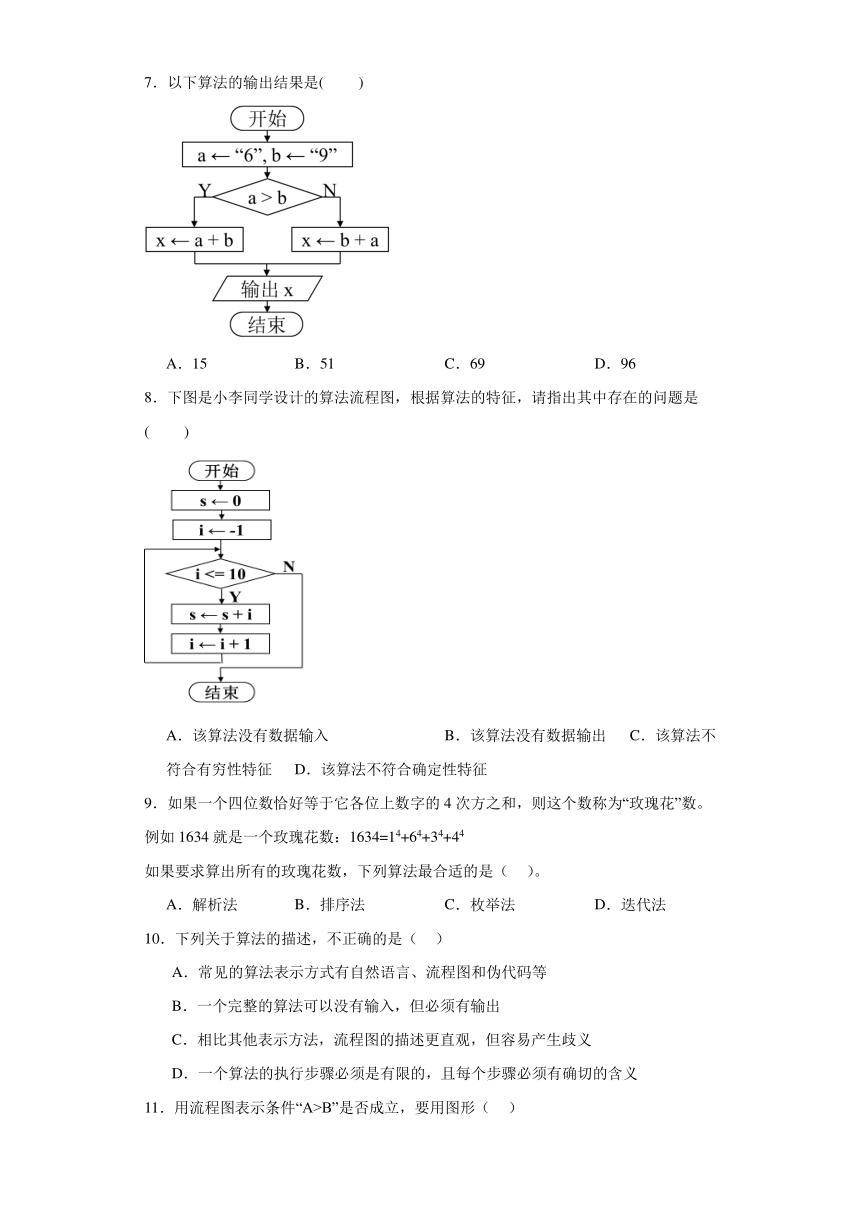
3.已知s="2023杭州亚运",则下列Python表达式中,值为True的是( )
A.s[1]=="2" B.s[2:4]==23 C.len(s)==7 D.54.某算法的部分流程图如图所示。若输入n的值为23,则输出sum的值为( )
A.2 B.3 C.4 D.5
5.下列关于计算机编程解决问题的一般过程的描述正确的是( )。
A.利用计算机可以直接自动识别并解决问题
B.设计算法、编写程序和运行调试是一个不断反复的过程
C.算法只要设计完成,就不需要更改
D.程序编译成功后一定是可执行的
6.该流程图的功能是:根据输入的正整数X,求分段函数
①处可填入的正确的表达式为( )
A.X%2==0 B.X%2!=0 C.int(X/2)== X/2 D.X%2== int(X/2)
7.以下算法的输出结果是( )
A.15 B.51 C.69 D.96
8.下图是小李同学设计的算法流程图,根据算法的特征,请指出其中存在的问题是( )
A.该算法没有数据输入 B.该算法没有数据输出 C.该算法不符合有穷性特征 D.该算法不符合确定性特征
9.如果一个四位数恰好等于它各位上数字的4次方之和,则这个数称为“玫瑰花”数。例如1634就是一个玫瑰花数:1634=14+64+34+44
如果要求算出所有的玫瑰花数,下列算法最合适的是( )。
A.解析法 B.排序法 C.枚举法 D.迭代法
10.下列关于算法的描述,不正确的是( )
A.常见的算法表示方式有自然语言、流程图和伪代码等
B.一个完整的算法可以没有输入,但必须有输出
C.相比其他表示方法,流程图的描述更直观,但容易产生歧义
D.一个算法的执行步骤必须是有限的,且每个步骤必须有确切的含义
11.用流程图表示条件“A>B”是否成立,要用图形( )
A. B. C. D.
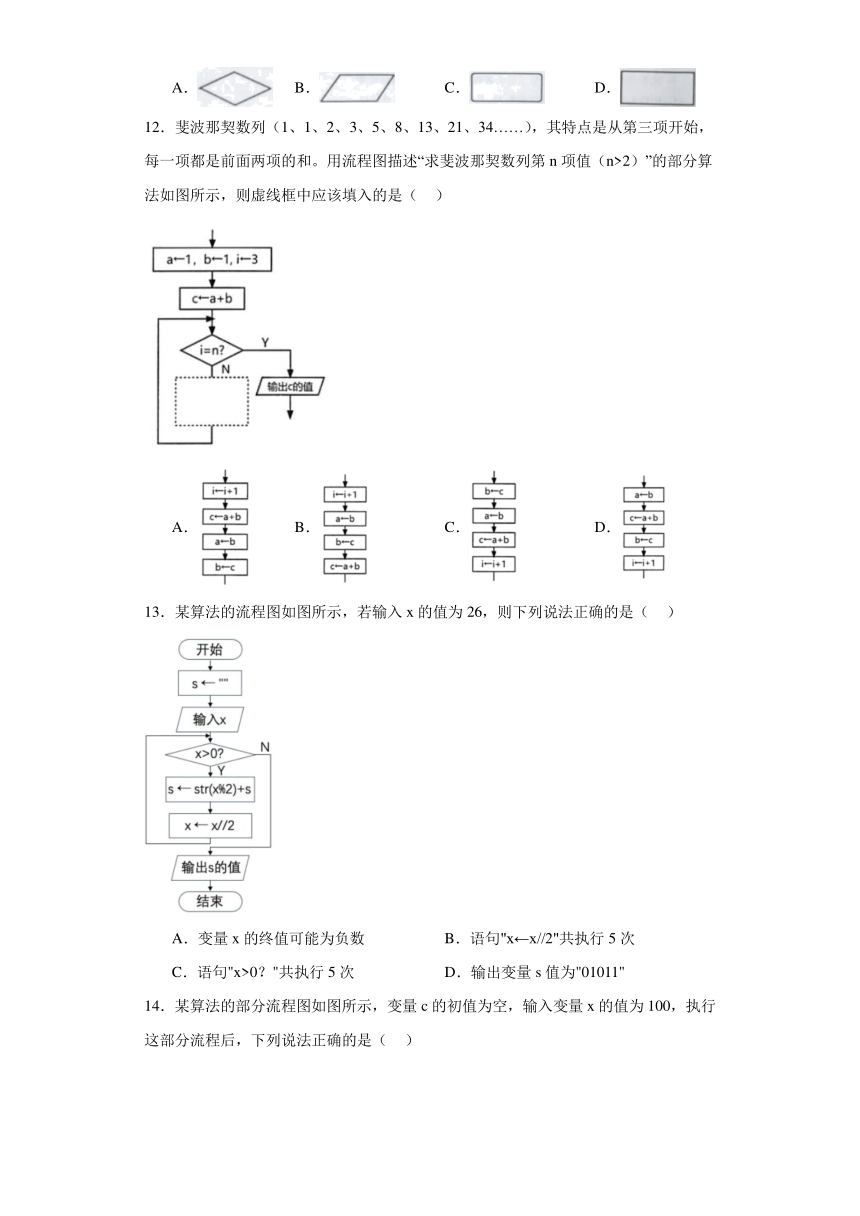
12.斐波那契数列(1、1、2、3、5、8、13、21、34……),其特点是从第三项开始,每一项都是前面两项的和。用流程图描述“求斐波那契数列第n项值(n>2)”的部分算法如图所示,则虚线框中应该填入的是( )
A. B. C. D.
13.某算法的流程图如图所示,若输入x的值为26,则下列说法正确的是( )
A.变量x的终值可能为负数 B.语句"x←x//2"共执行5次
C.语句"x>0?"共执行5次 D.输出变量s值为"01011"
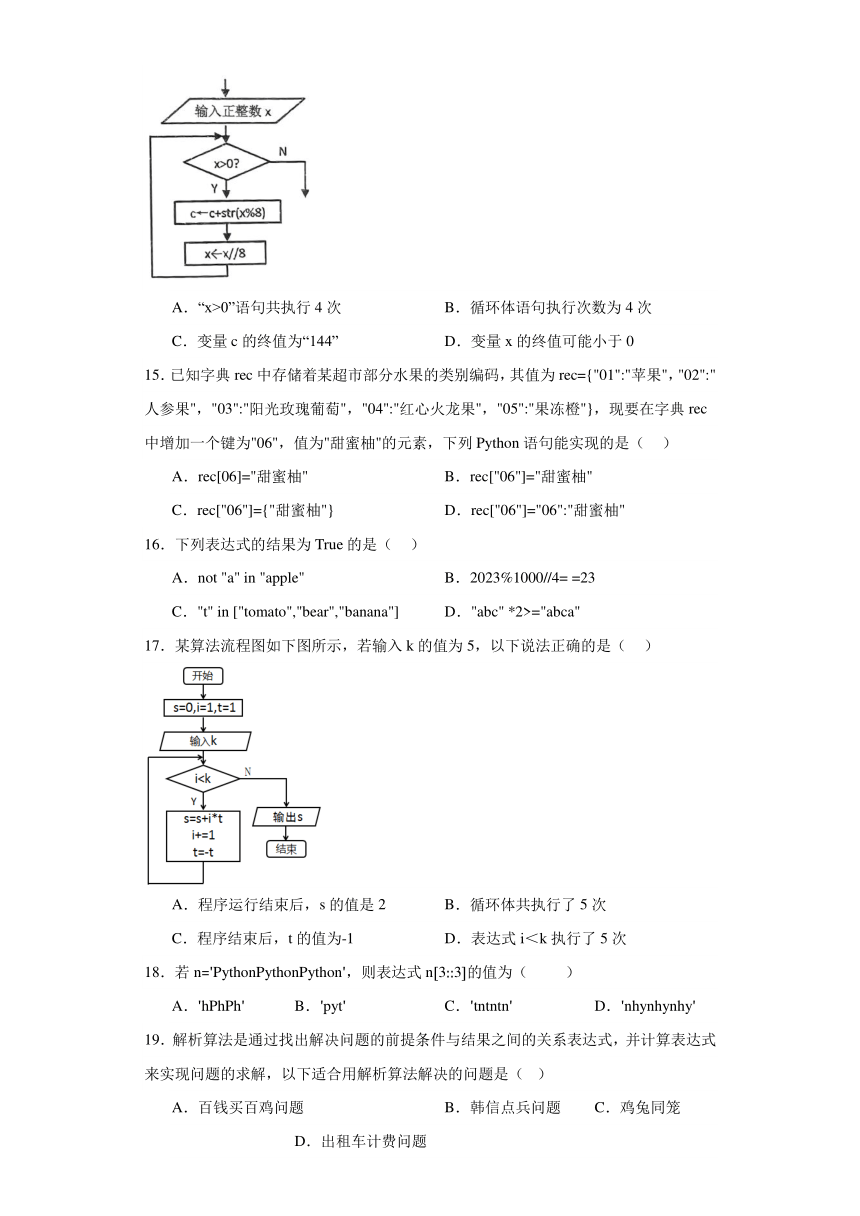
14.某算法的部分流程图如图所示,变量c的初值为空,输入变量x的值为100,执行这部分流程后,下列说法正确的是( )
A.“x>0”语句共执行4次 B.循环体语句执行次数为4次
C.变量c的终值为“144” D.变量x的终值可能小于0
15.已知字典rec中存储着某超市部分水果的类别编码,其值为rec={"01":"苹果","02":"人参果","03":"阳光玫瑰葡萄","04":"红心火龙果","05":"果冻橙"},现要在字典rec中增加一个键为"06",值为"甜蜜柚"的元素,下列Python语句能实现的是( )
A.rec[06]="甜蜜柚" B.rec["06"]="甜蜜柚"
C.rec["06"]={"甜蜜柚"} D.rec["06"]="06":"甜蜜柚"
16.下列表达式的结果为True的是( )
A.not "a" in "apple" B.2023%1000//4= =23
C."t" in ["tomato","bear","banana"] D."abc" *2>="abca"
17.某算法流程图如下图所示,若输入k的值为5,以下说法正确的是( )
A.程序运行结束后,s的值是2 B.循环体共执行了5次
C.程序结束后,t的值为-1 D.表达式i<k执行了5次
18.若n='PythonPythonPython',则表达式n[3::3]的值为( )
A.'hPhPh' B.'pyt' C.'tntntn' D.'nhynhynhy'
19.解析算法是通过找出解决问题的前提条件与结果之间的关系表达式,并计算表达式来实现问题的求解,以下适合用解析算法解决的问题是( )
A.百钱买百鸡问题 B.韩信点兵问题 C.鸡兔同笼 D.出租车计费问题
20.小申打算设计一个程序,能根据小时h,折算成秒s,利用计算机编写程序解决实际问题时,首先应该做的是( )
A.编写程序 B.设计算法 C.调试程序 D.抽象与建模
二、填空题
21..在Python中,(13%3)**2的结果是 。
22.在Python程序设计语言中,循环语句for i in range(1,9)中,变量的取值范围是 。
23.Python算术运算中求余数运算符用 表示。
24.在使用Python编写代码时,a减1的差对b(b不等于0)取余的正确表达式应该写为 。
25.某身份证号码s="33041120140203****"(后面4位用“*”表示),小丁想提取该身份证号码字符串中对应的出日期"20140203",在用Python语言实现的字符串操作中,以正索引方式获取出生日期子串的方法为
三、判断题
26.关系运算符运算结果一定是True或者False。( )
27.字符串的索引是从1开始的。( )
28.在 Python 程序设计语言中,表达式 11//2 的值为 1。( )
29.Python语言具有诸多优势,被广泛应用于科学计算、数据处理、人工智能等领域。( )
30.Python中提供内置函数和自定义函数等两种函数。( )
四、操作题
31.小丽打算利用假期出去旅游,为此她查阅了大量资料,在考虑费用、用时、便利程度等情况后,小丽决定乘坐高铁前往杭州旅游。
(1)在检票口检票进入站台上车时,小丽看到乘客刷了身份证闸机就开门了。小丽去查询了自助检票机的工作原理:刷身份证有购票记录就可以进去,车次不对和候车位置不对就进不去。小丽想到了用流程图来实现上述算法,请在以下选项中选出划线处的逻辑运算符是( )。
A.not B.and C.or
(2)通过流程图的结构,小丽开始整理描述算法会用到的结构。在算法描述中,用到了三种基本控制结构,分别是:顺序结构、分支结构、循环结构。那么第1题中的流程图使用到了哪些控制结构?( )。
A.顺序结构 B.分支结构 C.循环结构
(3)小丽去了西湖游玩,她看到边上有共享单车,打算骑车绕湖一圈。共享单车是通过扫描车架上的二维码进行租借,骑行结束,手动锁车后进行付费。下列有关共享单车的说法,不正确的是( )。
A.二维码是信息的载体 B.用户扫描二维码租车的过程属于信息的采集
C.为每一辆车设计二维码的过程属于信息的编码 D.生活中其他地方粘贴的二维码可以随意扫描
(4)小丽很喜欢西湖的景色,打算在酒店再续住一晚,打开酒店预定APP的时候发现酒店的价格比当初预定的时候更贵了一点,这主要体现的信息特征是( )。
A.载体依附性B.时效性C.共享性D.不确定性
(5)小丽到达一处景点,该旅游景点规定身高在1.2米以下的儿童免票,身高1.2~1.5 m(包含1.2 m和1.5 m)的儿童购买半票,身高超1.5 m的游客购买全票。实现上述算法的流程图如下,则划线处应该为?
① ②
(6)小丽想要能够记录下这次难忘的旅程,以下行为不属于数字化记录信息的是( )。
A.用手机拍摄西湖的照片 B.拍摄旅行VLOG C.将好吃的店铺记在手机备忘录里 D.手绘旅游攻略
32.进入新学期第一天,班主任老师将班上N个同学(学号为1-N)排成一排,分配座位。从排队到分配座位步骤如下:
步骤一:先将1号同学安排进队;
步骤二:2~N号同学由老师依次指定入队位置,如学号为i的同学由老师指定站在队中某位同学的左侧或右侧;
步骤三:所有同学按照上述方法入队完毕后,2人一组的方式依次分配到四个组别中;步骤四:输出每组学生的名单。
请回答下列问题。
(1)若某班有4位同学,学号为1~4,完成步骤一后,执行步骤二的指令3次,每次指令包含两个整数k和p(p为0或1)。若p为0,则表示插在k号同学的左侧,p为1则表示插在k号同学的右侧。若三条指令分别为1 0、2 1、1 0,则执行指令后队伍从左到右学号分别为: 。
(2)实现上述功能的部分Python程序如下,请在划线处填入合适的代码。
#insert (k, x)函数的功能是在k号的右侧插入x号同学;
#L和R列表分别用于记录每位同学的左侧和右侧的同学学号。
def insert (k,x):
R [x]=R [k]
L[x]=k
①
R [k]=x
L=[0]*100;R=[0]*l00;vis=[0]*100
insert (0,1) #0的右边插入1号同学
#info列表存储各学生姓名和学号,格式如[["张三",1],["李四",2]…],代码略
n=int (input ("请输入同学人数:"))
for i in range (2, n+1):
k=int (input ("请问插入在几号问学旁边?"))
p=int(input("请输入该同学的左侧还是右侧"))
if p= =0:
②
else:
insert (k, i)
q=[[] for i in range (4)]
i=m=0
③
while x!=0:
q[i].append(x)
m=m+l
if m%2= =0:
④
x=R[x]
for i in range(4):
for j in q[i]:
print (info [j-1][0],end=" ")
print()
33.某咖啡店,店里共有4种咖啡,类型编号为0到3,每次只能制作一种类型的咖啡,咖啡都是批量现做(制作过程中不能更改数量或类型)。店员需按照订单的先后顺序完成订单(即当前订单完成之前不能换订单)已经接到的订单中的同一类型咖啡可以一起制作(假设咖啡机能同时制作的数量上限足够高),且不需要额外增加时间(即只需制作一杯的时间)。如图15-1为每个订单的咖啡数量,初始″订单0″中[6,0,2,4]表示0到3号咖啡的购买数量。此时店员先做数量最多的6份0号咖啡,1分钟后接到新订单[1,18,0,2]之后每分钟都会接到1个新订单,这些订单都计入每种咖啡的待做数量。3分钟后这6份0号咖啡制作完成,程序会在″订单0″中选择还没制作的且待做数量最多的(数量相同时先后不作要求)咖啡作为下一次要制作的咖啡。编写python程序,每次制作完一种咖啡,输出接下来要制作的咖啡,运行界面如图15-2:
咖啡编号 订单编号 0 1 2 3 请制作咖啡0
0 6 0 2 4 请制作咖啡(1)
1 1 18 0 2 请制作咖啡2
2 2 1 2 1 请制作咖啡1
3 0 1 0 5 请制作咖啡3
…… 请制作咖啡2
请制作咖啡1
请制作咖啡0
图15-1 图15-2
(1)由图15-1的订单信息,3分钟后“咖啡0”制作完成,那么图15-2中(1)处店员接下来要做的咖啡是咖啡 。
(2)根据待制作的咖啡数量,对链表初始化,生成降序链表Ink,则代码运行后y的值为 。
def sort(): for i in range(3): for j in range(3,i,-1): if waitlist[index[j][1]>waitlist[index[j-1][1]: index[j],index[j-1]=index[j-1],index[j] if waitlist[index[i][1]]=0: return j return 4 waitlist=[[3,6],[4,0],[1,2],[2,4]] #″咖啡0″的批量制作时间为3分钟,目前待做量为6,以此类推 q=[6,0,2,4],[1,18,0,2],[2,1,2,1],[0,1,0,5],……#如图15-1,代码略 #q保存订单流,第一个订单[6,0,2,4]作为初始订单已计入waitlist index=[0,1,2,3] y=sort() Ink=[-1]*4 for i in range(y-1): #创建降序链表 Ink[index[i]]=index[i+1] p=Ink_h=index[0] print(″请制作咖啡″+str(p)) waitlist[p][1]=0 #咖啡p进入制作,待做数量0
(3)请在划线处填入合适的代码。
def enqueue(order): #order是一个订单,例如[1,2,0,3] global Ink_hflag.append([0,0,0,0]) #新订单4种咖啡未完成 for i in range(4): f=True if waitlist[i][1]=0:f=False if order[i]==0:continue waitlist[i][1]+=order[i] #将订单order中的咖啡i累加到待制作数量中 cur=Ink_h while cur!=-1 and waitlist[i][1]34.某酒店共有A、B、C三种房间型号,A、B、C型房间的住宿团队价分别为500元/晚、300元/晚、200元/晚。因房型和房间数量原因,酒店规定A型房间只能订1-9个,而B型和C型房间都必须订10-99个。每两个团队的订房信息共同组成一个订单码,该订单码以第一个团队编号″g1″和字符″-″开头,后面由房间型号及其数量组成,两个团队的信息编号以逗号分隔。例如,订单码″g1-A2B15C27,g2-A6B11C22″,表示团队g1所订A、B、C型房间的数量分别为2个、15个、27个,团队g2所订A、B、C型房间的数量分别为6个、11个、22个。请回答下列问题:
(1)若某订单码为″g1-A2B11C17,g2-A8B19C23″,则该订单一天住宿的总金额为 ①元。
(2)实现上述功能的部分Python程序如下,请在划线处填入合适的代码。
def fi(s,b,e):
income=0
i=b
while i<=e:
if s[i]=="A":
income+= ②
i+=2
elif s[i]=="B":
income+=int(s[i+1:i+3])*300
i+=3
elif s[i]=="C":
income+=int(s[i+1:i+3])*200
i+=3
return income
s=input("请输入订单码:")
flag=False
for i in range(len(s)):
if s[i]=="-"and not flag:
③
flag=True
elif s[i]=="-":
q=i
elif s[i]==",":
e=i
total=fi(s,p+1,e-1)
total+=fi(s, ④ ,len(s)-1)
print(total)
35.某文本编辑软件可以把所做的文本编辑操作记录下来,并通过撤销和恢复命令来撤销一步操作或恢复一步撤销的操作;也可以通过数字命令一次性撤销最近的多步文本编辑操作,如图所示。
设计算法模拟该功能。约定:①操作记录只存储文本编辑指令;②存储步数最多为5步,存满后早期的操作记录将被覆盖;③程序只显示操作记录的可“撤销”记录,可“恢复”记录不显示;④一旦有新的文本编辑操作,则清空所有可“恢复”记录。
人机交互的指令如下(所有操作示例都基于上一个示例结果继续操作):
所有指令均可使用多次。每次输入一个指令后都输出“F”指令和“B”指令是否可用以及当前可撤销记录。所有无效操作指令输入后均提示“Input Error!”。输入“#”则结束程序。请回答下列问题:
(1)由题意可知,当依次执行指令“T2”、“T2”、“T1”、“T3”、“T1”、“T4”,则最终可撤销记录共有 个。
(2)模拟实现该功能的Python代码如下,请在划线处填入合适的代码。
def printh(head,cur):
print(f[flag[0]*2+flag[1]])
s=″可撤销记录:″
while head!=cur+1:
s=s+hist[head]+″/″
print(s)
opera=[″T1″,″T2″,″T3″,″T4″]
f={0:″指令B不可用;指令F不可用″,1:″指令B不可用;指令F可用″,2:″指令B可用;指令F不可用″,3:″指令B可用;指令F可用″}
maxn=5 #历史记录最多存储的步数
maxsize=100 #设定最多输入文本编辑指令100次
hist=[″″]* maxsize
cur=-1;tail=0;head=0
flag=[0,0] #记录指令B与指令F的状态
while True:
d=input(″请输入操作指令:″)
if d==″#″:break
if d in opera:
if :
head=head+1
cur=cur+1; hist[cur]=d
tail=cur+1
flag=[1,0]
printh(head,cur)
elif″1″<=d<=str((cur-head+1)):
cur=
if cur==head-1:
flag[0]=0
flag[1]=1
printh(head,cur)
elif d==″F″and tail!=cur+1:
#恢复功能代码略
elif
if cur==head:flag[0]=0
flag[1]=1
cur=cur-1
printh(head,cur)
else:
print(″Input Error!″)
(3)若加框处代码误写为“d==″B″”,会导致某些情况下无法得到符合判断功能的结果。下列4组数据中能测试出这一问题的是
A.“B” B.“T1”、“B”、“B” C.“T1”、“1”、“B” D.“T1”、“T2”、“B”
参考答案
1.D
2.C
3.D
4.C
5.B
6.B
7.D
8.B
9.C
10.C
11.A
12.B
13.B
14.A
15.B
16.D
17.D
18.A
19.D
20.D
21.1
22.[1,8]
23.%
24.(a-1)%b
25.s[6:14]
26.正确
27.错误
28.错误
29.正确
30.正确
31. B AB D B h<1.2 h<1.5 D
32. 2341 L[R[k]]=x insert(L[k],i) x=R[0] i=(i+1)%4
33. 3 3 ①lnk[pr]=tmp ②cur!=-1and(q[qhead][cur]==0orflag[qhead][cur]==1) qhead, qtail或0,tail或qtail
34. 22000 int(s[i+1])*500 p=i q+1
35. 5 head+=1 cur-head+1==maxn或tail=cur+1 and tail-head==maxn cur-int(d) ABC
一、选择题
1.某算法的部分流程图如图所示,以下说法正确的是( )
A.若输入n的值为1,则无法输出“验证成功”的结果
B.该算法只有在输入n的值是偶数时,才能执行成功
C.若输入n的值为2,则“n≠1”的判断次数为1次
D.若输入n的值为5,则“n是偶数 ”的判断次数为5次
2.子序列是指数组中连续的若干个元素(至少1个元素)。数组a中有n个整型元素(有正有负),现要查找和最大的子序列,并输出和。实现该功能的程序段如下,方框中应填入的正确代码为( )
def maxsub(a):
tot=-1; tmp = 0
for num in a:
tmp += num
return tot
a = [-2,1,-3,4,-1,2,1,-5,4]
print(maxsub(a))
A. B. C. D.
3.已知s="2023杭州亚运",则下列Python表达式中,值为True的是( )
A.s[1]=="2" B.s[2:4]==23 C.len(s)==7 D.5
A.2 B.3 C.4 D.5
5.下列关于计算机编程解决问题的一般过程的描述正确的是( )。
A.利用计算机可以直接自动识别并解决问题
B.设计算法、编写程序和运行调试是一个不断反复的过程
C.算法只要设计完成,就不需要更改
D.程序编译成功后一定是可执行的
6.该流程图的功能是:根据输入的正整数X,求分段函数
①处可填入的正确的表达式为( )
A.X%2==0 B.X%2!=0 C.int(X/2)== X/2 D.X%2== int(X/2)
7.以下算法的输出结果是( )
A.15 B.51 C.69 D.96
8.下图是小李同学设计的算法流程图,根据算法的特征,请指出其中存在的问题是( )
A.该算法没有数据输入 B.该算法没有数据输出 C.该算法不符合有穷性特征 D.该算法不符合确定性特征
9.如果一个四位数恰好等于它各位上数字的4次方之和,则这个数称为“玫瑰花”数。例如1634就是一个玫瑰花数:1634=14+64+34+44
如果要求算出所有的玫瑰花数,下列算法最合适的是( )。
A.解析法 B.排序法 C.枚举法 D.迭代法
10.下列关于算法的描述,不正确的是( )
A.常见的算法表示方式有自然语言、流程图和伪代码等
B.一个完整的算法可以没有输入,但必须有输出
C.相比其他表示方法,流程图的描述更直观,但容易产生歧义
D.一个算法的执行步骤必须是有限的,且每个步骤必须有确切的含义
11.用流程图表示条件“A>B”是否成立,要用图形( )
A. B. C. D.
12.斐波那契数列(1、1、2、3、5、8、13、21、34……),其特点是从第三项开始,每一项都是前面两项的和。用流程图描述“求斐波那契数列第n项值(n>2)”的部分算法如图所示,则虚线框中应该填入的是( )
A. B. C. D.
13.某算法的流程图如图所示,若输入x的值为26,则下列说法正确的是( )
A.变量x的终值可能为负数 B.语句"x←x//2"共执行5次
C.语句"x>0?"共执行5次 D.输出变量s值为"01011"
14.某算法的部分流程图如图所示,变量c的初值为空,输入变量x的值为100,执行这部分流程后,下列说法正确的是( )
A.“x>0”语句共执行4次 B.循环体语句执行次数为4次
C.变量c的终值为“144” D.变量x的终值可能小于0
15.已知字典rec中存储着某超市部分水果的类别编码,其值为rec={"01":"苹果","02":"人参果","03":"阳光玫瑰葡萄","04":"红心火龙果","05":"果冻橙"},现要在字典rec中增加一个键为"06",值为"甜蜜柚"的元素,下列Python语句能实现的是( )
A.rec[06]="甜蜜柚" B.rec["06"]="甜蜜柚"
C.rec["06"]={"甜蜜柚"} D.rec["06"]="06":"甜蜜柚"
16.下列表达式的结果为True的是( )
A.not "a" in "apple" B.2023%1000//4= =23
C."t" in ["tomato","bear","banana"] D."abc" *2>="abca"
17.某算法流程图如下图所示,若输入k的值为5,以下说法正确的是( )
A.程序运行结束后,s的值是2 B.循环体共执行了5次
C.程序结束后,t的值为-1 D.表达式i<k执行了5次
18.若n='PythonPythonPython',则表达式n[3::3]的值为( )
A.'hPhPh' B.'pyt' C.'tntntn' D.'nhynhynhy'
19.解析算法是通过找出解决问题的前提条件与结果之间的关系表达式,并计算表达式来实现问题的求解,以下适合用解析算法解决的问题是( )
A.百钱买百鸡问题 B.韩信点兵问题 C.鸡兔同笼 D.出租车计费问题
20.小申打算设计一个程序,能根据小时h,折算成秒s,利用计算机编写程序解决实际问题时,首先应该做的是( )
A.编写程序 B.设计算法 C.调试程序 D.抽象与建模
二、填空题
21..在Python中,(13%3)**2的结果是 。
22.在Python程序设计语言中,循环语句for i in range(1,9)中,变量的取值范围是 。
23.Python算术运算中求余数运算符用 表示。
24.在使用Python编写代码时,a减1的差对b(b不等于0)取余的正确表达式应该写为 。
25.某身份证号码s="33041120140203****"(后面4位用“*”表示),小丁想提取该身份证号码字符串中对应的出日期"20140203",在用Python语言实现的字符串操作中,以正索引方式获取出生日期子串的方法为
三、判断题
26.关系运算符运算结果一定是True或者False。( )
27.字符串的索引是从1开始的。( )
28.在 Python 程序设计语言中,表达式 11//2 的值为 1。( )
29.Python语言具有诸多优势,被广泛应用于科学计算、数据处理、人工智能等领域。( )
30.Python中提供内置函数和自定义函数等两种函数。( )
四、操作题
31.小丽打算利用假期出去旅游,为此她查阅了大量资料,在考虑费用、用时、便利程度等情况后,小丽决定乘坐高铁前往杭州旅游。
(1)在检票口检票进入站台上车时,小丽看到乘客刷了身份证闸机就开门了。小丽去查询了自助检票机的工作原理:刷身份证有购票记录就可以进去,车次不对和候车位置不对就进不去。小丽想到了用流程图来实现上述算法,请在以下选项中选出划线处的逻辑运算符是( )。
A.not B.and C.or
(2)通过流程图的结构,小丽开始整理描述算法会用到的结构。在算法描述中,用到了三种基本控制结构,分别是:顺序结构、分支结构、循环结构。那么第1题中的流程图使用到了哪些控制结构?( )。
A.顺序结构 B.分支结构 C.循环结构
(3)小丽去了西湖游玩,她看到边上有共享单车,打算骑车绕湖一圈。共享单车是通过扫描车架上的二维码进行租借,骑行结束,手动锁车后进行付费。下列有关共享单车的说法,不正确的是( )。
A.二维码是信息的载体 B.用户扫描二维码租车的过程属于信息的采集
C.为每一辆车设计二维码的过程属于信息的编码 D.生活中其他地方粘贴的二维码可以随意扫描
(4)小丽很喜欢西湖的景色,打算在酒店再续住一晚,打开酒店预定APP的时候发现酒店的价格比当初预定的时候更贵了一点,这主要体现的信息特征是( )。
A.载体依附性B.时效性C.共享性D.不确定性
(5)小丽到达一处景点,该旅游景点规定身高在1.2米以下的儿童免票,身高1.2~1.5 m(包含1.2 m和1.5 m)的儿童购买半票,身高超1.5 m的游客购买全票。实现上述算法的流程图如下,则划线处应该为?
① ②
(6)小丽想要能够记录下这次难忘的旅程,以下行为不属于数字化记录信息的是( )。
A.用手机拍摄西湖的照片 B.拍摄旅行VLOG C.将好吃的店铺记在手机备忘录里 D.手绘旅游攻略
32.进入新学期第一天,班主任老师将班上N个同学(学号为1-N)排成一排,分配座位。从排队到分配座位步骤如下:
步骤一:先将1号同学安排进队;
步骤二:2~N号同学由老师依次指定入队位置,如学号为i的同学由老师指定站在队中某位同学的左侧或右侧;
步骤三:所有同学按照上述方法入队完毕后,2人一组的方式依次分配到四个组别中;步骤四:输出每组学生的名单。
请回答下列问题。
(1)若某班有4位同学,学号为1~4,完成步骤一后,执行步骤二的指令3次,每次指令包含两个整数k和p(p为0或1)。若p为0,则表示插在k号同学的左侧,p为1则表示插在k号同学的右侧。若三条指令分别为1 0、2 1、1 0,则执行指令后队伍从左到右学号分别为: 。
(2)实现上述功能的部分Python程序如下,请在划线处填入合适的代码。
#insert (k, x)函数的功能是在k号的右侧插入x号同学;
#L和R列表分别用于记录每位同学的左侧和右侧的同学学号。
def insert (k,x):
R [x]=R [k]
L[x]=k
①
R [k]=x
L=[0]*100;R=[0]*l00;vis=[0]*100
insert (0,1) #0的右边插入1号同学
#info列表存储各学生姓名和学号,格式如[["张三",1],["李四",2]…],代码略
n=int (input ("请输入同学人数:"))
for i in range (2, n+1):
k=int (input ("请问插入在几号问学旁边?"))
p=int(input("请输入该同学的左侧还是右侧"))
if p= =0:
②
else:
insert (k, i)
q=[[] for i in range (4)]
i=m=0
③
while x!=0:
q[i].append(x)
m=m+l
if m%2= =0:
④
x=R[x]
for i in range(4):
for j in q[i]:
print (info [j-1][0],end=" ")
print()
33.某咖啡店,店里共有4种咖啡,类型编号为0到3,每次只能制作一种类型的咖啡,咖啡都是批量现做(制作过程中不能更改数量或类型)。店员需按照订单的先后顺序完成订单(即当前订单完成之前不能换订单)已经接到的订单中的同一类型咖啡可以一起制作(假设咖啡机能同时制作的数量上限足够高),且不需要额外增加时间(即只需制作一杯的时间)。如图15-1为每个订单的咖啡数量,初始″订单0″中[6,0,2,4]表示0到3号咖啡的购买数量。此时店员先做数量最多的6份0号咖啡,1分钟后接到新订单[1,18,0,2]之后每分钟都会接到1个新订单,这些订单都计入每种咖啡的待做数量。3分钟后这6份0号咖啡制作完成,程序会在″订单0″中选择还没制作的且待做数量最多的(数量相同时先后不作要求)咖啡作为下一次要制作的咖啡。编写python程序,每次制作完一种咖啡,输出接下来要制作的咖啡,运行界面如图15-2:
咖啡编号 订单编号 0 1 2 3 请制作咖啡0
0 6 0 2 4 请制作咖啡(1)
1 1 18 0 2 请制作咖啡2
2 2 1 2 1 请制作咖啡1
3 0 1 0 5 请制作咖啡3
…… 请制作咖啡2
请制作咖啡1
请制作咖啡0
图15-1 图15-2
(1)由图15-1的订单信息,3分钟后“咖啡0”制作完成,那么图15-2中(1)处店员接下来要做的咖啡是咖啡 。
(2)根据待制作的咖啡数量,对链表初始化,生成降序链表Ink,则代码运行后y的值为 。
def sort(): for i in range(3): for j in range(3,i,-1): if waitlist[index[j][1]>waitlist[index[j-1][1]: index[j],index[j-1]=index[j-1],index[j] if waitlist[index[i][1]]=0: return j return 4 waitlist=[[3,6],[4,0],[1,2],[2,4]] #″咖啡0″的批量制作时间为3分钟,目前待做量为6,以此类推 q=[6,0,2,4],[1,18,0,2],[2,1,2,1],[0,1,0,5],……#如图15-1,代码略 #q保存订单流,第一个订单[6,0,2,4]作为初始订单已计入waitlist index=[0,1,2,3] y=sort() Ink=[-1]*4 for i in range(y-1): #创建降序链表 Ink[index[i]]=index[i+1] p=Ink_h=index[0] print(″请制作咖啡″+str(p)) waitlist[p][1]=0 #咖啡p进入制作,待做数量0
(3)请在划线处填入合适的代码。
def enqueue(order): #order是一个订单,例如[1,2,0,3] global Ink_hflag.append([0,0,0,0]) #新订单4种咖啡未完成 for i in range(4): f=True if waitlist[i][1]=0:f=False if order[i]==0:continue waitlist[i][1]+=order[i] #将订单order中的咖啡i累加到待制作数量中 cur=Ink_h while cur!=-1 and waitlist[i][1]
(1)若某订单码为″g1-A2B11C17,g2-A8B19C23″,则该订单一天住宿的总金额为 ①元。
(2)实现上述功能的部分Python程序如下,请在划线处填入合适的代码。
def fi(s,b,e):
income=0
i=b
while i<=e:
if s[i]=="A":
income+= ②
i+=2
elif s[i]=="B":
income+=int(s[i+1:i+3])*300
i+=3
elif s[i]=="C":
income+=int(s[i+1:i+3])*200
i+=3
return income
s=input("请输入订单码:")
flag=False
for i in range(len(s)):
if s[i]=="-"and not flag:
③
flag=True
elif s[i]=="-":
q=i
elif s[i]==",":
e=i
total=fi(s,p+1,e-1)
total+=fi(s, ④ ,len(s)-1)
print(total)
35.某文本编辑软件可以把所做的文本编辑操作记录下来,并通过撤销和恢复命令来撤销一步操作或恢复一步撤销的操作;也可以通过数字命令一次性撤销最近的多步文本编辑操作,如图所示。
设计算法模拟该功能。约定:①操作记录只存储文本编辑指令;②存储步数最多为5步,存满后早期的操作记录将被覆盖;③程序只显示操作记录的可“撤销”记录,可“恢复”记录不显示;④一旦有新的文本编辑操作,则清空所有可“恢复”记录。
人机交互的指令如下(所有操作示例都基于上一个示例结果继续操作):
所有指令均可使用多次。每次输入一个指令后都输出“F”指令和“B”指令是否可用以及当前可撤销记录。所有无效操作指令输入后均提示“Input Error!”。输入“#”则结束程序。请回答下列问题:
(1)由题意可知,当依次执行指令“T2”、“T2”、“T1”、“T3”、“T1”、“T4”,则最终可撤销记录共有 个。
(2)模拟实现该功能的Python代码如下,请在划线处填入合适的代码。
def printh(head,cur):
print(f[flag[0]*2+flag[1]])
s=″可撤销记录:″
while head!=cur+1:
s=s+hist[head]+″/″
print(s)
opera=[″T1″,″T2″,″T3″,″T4″]
f={0:″指令B不可用;指令F不可用″,1:″指令B不可用;指令F可用″,2:″指令B可用;指令F不可用″,3:″指令B可用;指令F可用″}
maxn=5 #历史记录最多存储的步数
maxsize=100 #设定最多输入文本编辑指令100次
hist=[″″]* maxsize
cur=-1;tail=0;head=0
flag=[0,0] #记录指令B与指令F的状态
while True:
d=input(″请输入操作指令:″)
if d==″#″:break
if d in opera:
if :
head=head+1
cur=cur+1; hist[cur]=d
tail=cur+1
flag=[1,0]
printh(head,cur)
elif″1″<=d<=str((cur-head+1)):
cur=
if cur==head-1:
flag[0]=0
flag[1]=1
printh(head,cur)
elif d==″F″and tail!=cur+1:
#恢复功能代码略
elif
if cur==head:flag[0]=0
flag[1]=1
cur=cur-1
printh(head,cur)
else:
print(″Input Error!″)
(3)若加框处代码误写为“d==″B″”,会导致某些情况下无法得到符合判断功能的结果。下列4组数据中能测试出这一问题的是
A.“B” B.“T1”、“B”、“B” C.“T1”、“1”、“B” D.“T1”、“T2”、“B”
参考答案
1.D
2.C
3.D
4.C
5.B
6.B
7.D
8.B
9.C
10.C
11.A
12.B
13.B
14.A
15.B
16.D
17.D
18.A
19.D
20.D
21.1
22.[1,8]
23.%
24.(a-1)%b
25.s[6:14]
26.正确
27.错误
28.错误
29.正确
30.正确
31. B AB D B h<1.2 h<1.5 D
32. 2341 L[R[k]]=x insert(L[k],i) x=R[0] i=(i+1)%4
33. 3 3 ①lnk[pr]=tmp ②cur!=-1and(q[qhead][cur]==0orflag[qhead][cur]==1) qhead, qtail或0,tail或qtail
34. 22000 int(s[i+1])*500 p=i q+1
35. 5 head+=1 cur-head+1==maxn或tail=cur+1 and tail-head==maxn cur-int(d) ABC
同课章节目录
- 第1章 认识数据与大数据
- 主题学习项目:体质数据促健康
- 1.1 数据、信息与知识
- 1.2 数字化与编码
- 1.3 数据科学与大数据
- 第2章 算法与程序实现
- 主题学习项目:编程控灯利出行
- 2.1 解决问题的一般过程和用计算机解决问题
- 2.2 算法的概念及描述
- 2.3 程序设计基本知识
- 2.4 常见算法的程序实现
- 第3章 数据处理与应用
- 主题学习项目:用水分析助决策
- 3.1 数据处理的一般过程
- 3.2 数据采集与整理
- 3.3 数据分析与可视化
- 3.4 数据分析报告与应用
- 第4章 走进智能时代
- 主题学习项目:智能交互益拓展
- 4.1 认识人工智能
- 4.2 利用智能工具解决问题
- 4.3 人工智能的应用与影响
