数学人教A版(2019)必修第一册3.4.1方程的根与函数的零点 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.4.1方程的根与函数的零点 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 19:19:43 | ||
图片预览








文档简介
(共25张PPT)
为了变成第一名
天天提着一口气
为了完成数学题
熬夜熬成熊猫精
学霸学霸教教我
这道题该怎么做
努力 我要努力
我要变成第一名
◎
燃烧我的数学题
数学题数学题数学题
数学题数学题数学题
数学题数学题数学题
数学题我的天敌
燃烧我的数学题
1650年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。后来,笛卡尔成为了公主的数学老师,并且与公主相恋了。然而,没过多久,他们的恋情就传到了国王的耳朵里。国王勃然大怒,下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下,国王将他放逐回法国,公主也被软禁在宫中。
当时,欧洲大陆正在流行黑死病。体弱的笛卡尔回到法国后不久,便染上重病。在生命进入倒计时的日子里,他日夜思念着公主。并每天坚持给她写信。
在笛卡尔寄出第十三封信后,他便永远地离开了这个世界。
笛卡尔寄出的最后一封信是:
至今,仍然保存在欧洲笛卡尔的纪念馆里。
心
形
线
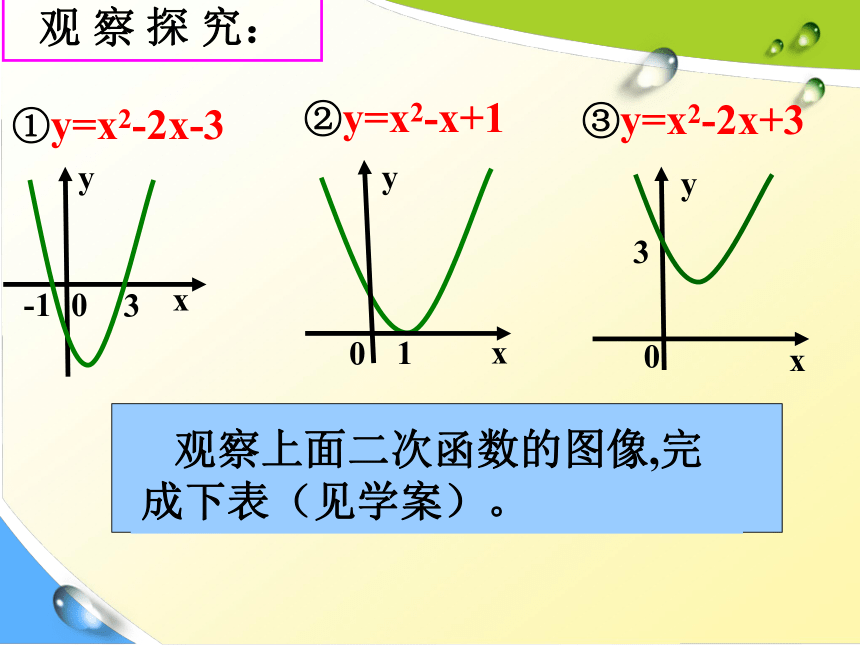
①y=x2-2x-3
②y=x2-x+1
③y=x2-2x+3
观 察 探 究:
观察上面二次函数的图像,完成下表(见学案)。
x
3
3
-1
0
y
0
1
x
y
y
x
0
观 察 汇 总
将以上观察结果汇总填表
函数与x轴交点的横坐标
二次方程
二次函数
方程的根
函数与x轴交点
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
y=x2-2x+3
y=x2-2x+1
y=x2-2x-3
无交点
x1=-1,x2=3
x1=x2=1
无交点
无实根
(-1,0),(3,0)
(1,0)
-1,3
1
函数的
零 点
是否等价
新知识 点拨
函数零点的概念:
对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点。
课题:方程的根与函数的零点
函数与x轴交点的横坐标
二次方程
二次函数
方程的根
函数与x轴交点
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
y=x2-2x+3
y=x2-2x+1
y=x2-2x-3
无交点
x1=-1,x2=3
x1=x2=1
无交点
无实根
(-1,0),(3,0)
(1,0)
-1,3
1
函数的零 点
新知识 点拨
方程f(x)=0有实数根
函数y=f(x)的图像与x轴有交点
函数y=f(x)有零点
课题:方程的根与函数的零点
对于函数y=f(x),把使f(x)=0的 x 叫做函数y=f(x)的零点。
练习2 已知函数f(x)的图像,则函数的零点是 .
练习1 函数f(x)=x2-2x-3的零点是 .
-2
-3
-4
-1
1
2
●
●
●
●
●
●
y=f(x)
方程f(x)=0有实数根
函数y=f(x)的图像与x轴有交点
函数y=f(x)有零点
课题:方程的根与函数的零点
实数
反思归纳:
(1)零点不是点,零点是个数。
(2)求零点的方法有:解方程和图像
观 察 探 究
-2
-4
-3
-1
1
2
●
●
●
●
●
y=f(x)
●
3
●
课题:方程的根与函数的零点
动 手 操 作
用一条连续不断的曲线将A,B两点连接起来,并观察在区间[a,b]上零点存在的情况。
b
a
A●
●
B
b
a
B
●
●
b
a
A
●
B●
b
a
●
A
●
B
(1)
(2)
(3)
(4)
课题:方程的根与函数的零点
探 索:函数f(x)在区间[a,b]上有定义,则在(a,b)上一定有零点需要哪些条件?
结 论 探 索
课题:方程的根与函数的零点
新知识 点拨
练习3函数y=f(x)在区间[a,b]上的是连续不断的一条曲线,并且f(a).f(b)<0,则这个函数在这个区间上 ( )
A.只有一个零点 B.至多有一个零点
C.至少有一个零点 D.不一定有零点
零点存在性定理:如果函数y=f(x)在区间[a,b]上的图像是 的一条曲线, 并且有 那么,函数y=f(x)在区间(a,b) 上 零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
至少一个
有
连续不断
f(a).f(b)<0
课题:方程的根与函数的零点
新知识 点拨
变式:如果练习3的条件不变,为确保零点的唯一性,需要增加什么条件?
练习3函数y=f(x)在区间[a,b]上的是连续不断的一条曲线,并且f(a)●f(b)<0,则这个函数在这个区间上 ( )
A.只有一个零点 B.至多有一个零点
C.至少有一个零点 D.不一定有零点
在练习3的条件不变的情况下,增加函数在[a,b]上还具有单调性,则函数在(a,b)上有唯一零点
课题:方程的根与函数的零点
新知识 点拨
在零点存在性定理中若f(a)●f(b)<0,则函数在(a,b)一定有零点,请问若函数在(a,b)内有零点就一定有f(a)●f(b)<0成立吗?
课题:方程的根与函数的零点
例题1
(1)函数f(x)=2x+x-2在(0,1)内的零点个数是( )
(A) 0 (B)1 (C)2 (D)3
(2)f(x)=(x2-9)(2x-4)的零点个数是( )
(A) 0 (B)1 (C)2 (D)3
课题:方程的根与函数的零点
反思归纳(求解零点的方法有):
(1)存在性定理
(2)图像
(3)方程
祝
愿
同
学
们
学
习
进
步
,
快
乐
成
长
学
习
进
步
,
快
乐
成
长
谢谢!
课 堂 小 结
3 对于本节课的学习,你还有哪些疑问?
方程的根与函数的零点
(1)函数的零点的值就是方程的根的值,也是函数与x轴交点的横坐标的值。那么,函数的零点、方程的根及函数与x轴交点的横坐标是否也是等价关系?
(2)对函数零点的存在性定理理解中,函数在(a,b)有零点f(a).f(b)<0不一定成立。那么,我们能否添加条件使得“函数在(a,b)有零点,f(a).f(b)<0也成立”
(3)通过这件课的学习我们知道方程lnx+2x-6=0有唯一实数根,那么,这个根是多少呢?
学 习 目 标:
(1)了解函数零点的概念
(3)会判断函数零点所在的区间
及个数
(2)理解函数零点与方程的根之间
的关系
课题:方程的根与函数的零点
1 请你说说方程的根与函数零点的关系。
2 对零点存在性定理你有何理解?
课 堂 小 结
3 对于本节课的学习,你还有哪些疑问?
课题:方程的根与函数的零点
例题1 求函数f(x)=lnx+2x-6的零点个数。
因为f(1)= -2<0,f(3)=ln3>0,
所以f(1).f(3)<0,
所以f(x)在(1,3)上是增函数
所以,f(x)在区间(1,3)仅有一个零点.
y=lnx 是增函数,
y=2x-6 也是增函数,
(-1,1) ,(1,3) ,( 3,5)
课题:方程的根与函数的零点
解:
例题1 求函数f(x)=lnx+2x-6的零点个数。
解二 : 函数f(x)=lnx+2x-6的零点个数,就是方程lnx+2x-6=0的根的个数,
也就是函数y=lnx与函数y=-2x+6交点的个数,
所以,f(x)在区间(1,3)仅有一个零点.
●
●
●
●
●
●
●
●
●
6
5
3
2
1
4
1
2
3
y=lnx
y=-2x+6
●
课题:方程的根与函数的零点
祝
愿
同
学
们
学
习
进
步
,
快
乐
成
长
学
习
进
步
,
快
乐
成
长
谢谢!
为了变成第一名
天天提着一口气
为了完成数学题
熬夜熬成熊猫精
学霸学霸教教我
这道题该怎么做
努力 我要努力
我要变成第一名
◎
燃烧我的数学题
数学题数学题数学题
数学题数学题数学题
数学题数学题数学题
数学题我的天敌
燃烧我的数学题
1650年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。后来,笛卡尔成为了公主的数学老师,并且与公主相恋了。然而,没过多久,他们的恋情就传到了国王的耳朵里。国王勃然大怒,下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下,国王将他放逐回法国,公主也被软禁在宫中。
当时,欧洲大陆正在流行黑死病。体弱的笛卡尔回到法国后不久,便染上重病。在生命进入倒计时的日子里,他日夜思念着公主。并每天坚持给她写信。
在笛卡尔寄出第十三封信后,他便永远地离开了这个世界。
笛卡尔寄出的最后一封信是:
至今,仍然保存在欧洲笛卡尔的纪念馆里。
心
形
线
①y=x2-2x-3
②y=x2-x+1
③y=x2-2x+3
观 察 探 究:
观察上面二次函数的图像,完成下表(见学案)。
x
3
3
-1
0
y
0
1
x
y
y
x
0
观 察 汇 总
将以上观察结果汇总填表
函数与x轴交点的横坐标
二次方程
二次函数
方程的根
函数与x轴交点
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
y=x2-2x+3
y=x2-2x+1
y=x2-2x-3
无交点
x1=-1,x2=3
x1=x2=1
无交点
无实根
(-1,0),(3,0)
(1,0)
-1,3
1
函数的
零 点
是否等价
新知识 点拨
函数零点的概念:
对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点。
课题:方程的根与函数的零点
函数与x轴交点的横坐标
二次方程
二次函数
方程的根
函数与x轴交点
x2-2x-3=0
x2-2x+1=0
x2-2x+3=0
y=x2-2x+3
y=x2-2x+1
y=x2-2x-3
无交点
x1=-1,x2=3
x1=x2=1
无交点
无实根
(-1,0),(3,0)
(1,0)
-1,3
1
函数的零 点
新知识 点拨
方程f(x)=0有实数根
函数y=f(x)的图像与x轴有交点
函数y=f(x)有零点
课题:方程的根与函数的零点
对于函数y=f(x),把使f(x)=0的 x 叫做函数y=f(x)的零点。
练习2 已知函数f(x)的图像,则函数的零点是 .
练习1 函数f(x)=x2-2x-3的零点是 .
-2
-3
-4
-1
1
2
●
●
●
●
●
●
y=f(x)
方程f(x)=0有实数根
函数y=f(x)的图像与x轴有交点
函数y=f(x)有零点
课题:方程的根与函数的零点
实数
反思归纳:
(1)零点不是点,零点是个数。
(2)求零点的方法有:解方程和图像
观 察 探 究
-2
-4
-3
-1
1
2
●
●
●
●
●
y=f(x)
●
3
●
课题:方程的根与函数的零点
动 手 操 作
用一条连续不断的曲线将A,B两点连接起来,并观察在区间[a,b]上零点存在的情况。
b
a
A●
●
B
b
a
B
●
●
b
a
A
●
B●
b
a
●
A
●
B
(1)
(2)
(3)
(4)
课题:方程的根与函数的零点
探 索:函数f(x)在区间[a,b]上有定义,则在(a,b)上一定有零点需要哪些条件?
结 论 探 索
课题:方程的根与函数的零点
新知识 点拨
练习3函数y=f(x)在区间[a,b]上的是连续不断的一条曲线,并且f(a).f(b)<0,则这个函数在这个区间上 ( )
A.只有一个零点 B.至多有一个零点
C.至少有一个零点 D.不一定有零点
零点存在性定理:如果函数y=f(x)在区间[a,b]上的图像是 的一条曲线, 并且有 那么,函数y=f(x)在区间(a,b) 上 零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根。
至少一个
有
连续不断
f(a).f(b)<0
课题:方程的根与函数的零点
新知识 点拨
变式:如果练习3的条件不变,为确保零点的唯一性,需要增加什么条件?
练习3函数y=f(x)在区间[a,b]上的是连续不断的一条曲线,并且f(a)●f(b)<0,则这个函数在这个区间上 ( )
A.只有一个零点 B.至多有一个零点
C.至少有一个零点 D.不一定有零点
在练习3的条件不变的情况下,增加函数在[a,b]上还具有单调性,则函数在(a,b)上有唯一零点
课题:方程的根与函数的零点
新知识 点拨
在零点存在性定理中若f(a)●f(b)<0,则函数在(a,b)一定有零点,请问若函数在(a,b)内有零点就一定有f(a)●f(b)<0成立吗?
课题:方程的根与函数的零点
例题1
(1)函数f(x)=2x+x-2在(0,1)内的零点个数是( )
(A) 0 (B)1 (C)2 (D)3
(2)f(x)=(x2-9)(2x-4)的零点个数是( )
(A) 0 (B)1 (C)2 (D)3
课题:方程的根与函数的零点
反思归纳(求解零点的方法有):
(1)存在性定理
(2)图像
(3)方程
祝
愿
同
学
们
学
习
进
步
,
快
乐
成
长
学
习
进
步
,
快
乐
成
长
谢谢!
课 堂 小 结
3 对于本节课的学习,你还有哪些疑问?
方程的根与函数的零点
(1)函数的零点的值就是方程的根的值,也是函数与x轴交点的横坐标的值。那么,函数的零点、方程的根及函数与x轴交点的横坐标是否也是等价关系?
(2)对函数零点的存在性定理理解中,函数在(a,b)有零点f(a).f(b)<0不一定成立。那么,我们能否添加条件使得“函数在(a,b)有零点,f(a).f(b)<0也成立”
(3)通过这件课的学习我们知道方程lnx+2x-6=0有唯一实数根,那么,这个根是多少呢?
学 习 目 标:
(1)了解函数零点的概念
(3)会判断函数零点所在的区间
及个数
(2)理解函数零点与方程的根之间
的关系
课题:方程的根与函数的零点
1 请你说说方程的根与函数零点的关系。
2 对零点存在性定理你有何理解?
课 堂 小 结
3 对于本节课的学习,你还有哪些疑问?
课题:方程的根与函数的零点
例题1 求函数f(x)=lnx+2x-6的零点个数。
因为f(1)= -2<0,f(3)=ln3>0,
所以f(1).f(3)<0,
所以f(x)在(1,3)上是增函数
所以,f(x)在区间(1,3)仅有一个零点.
y=lnx 是增函数,
y=2x-6 也是增函数,
(-1,1) ,(1,3) ,( 3,5)
课题:方程的根与函数的零点
解:
例题1 求函数f(x)=lnx+2x-6的零点个数。
解二 : 函数f(x)=lnx+2x-6的零点个数,就是方程lnx+2x-6=0的根的个数,
也就是函数y=lnx与函数y=-2x+6交点的个数,
所以,f(x)在区间(1,3)仅有一个零点.
●
●
●
●
●
●
●
●
●
6
5
3
2
1
4
1
2
3
y=lnx
y=-2x+6
●
课题:方程的根与函数的零点
祝
愿
同
学
们
学
习
进
步
,
快
乐
成
长
学
习
进
步
,
快
乐
成
长
谢谢!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
