2023-2024学年沪科版(2012)七年级上册第四章直线与角单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年沪科版(2012)七年级上册第四章直线与角单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 548.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览




文档简介
2023-2024学年 沪科版(2012)七年级上册 第四章 直线与角 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,C、D是线段上两点,M、N分别是线段、的中点,下列结论:①若,则;②若,则;③;④.其中正确的结论是( )
A.①②③ B.③④ C.①②④ D.①②③④
2.下列说法中:(1)x是单项式;(2)多项式的次数是4;(3)的常数项是1;(4)由两条射线组成的图形叫做角,正确的个数是( )
A.0个 B.1个 C.2个 D.3个
3.如图是一个正方体盒子展开后的平面图形,六个面上分别写有“数”、“学”、“核”“心”、“素”、“养”,则“素”字对面的字是( )
A.核 B.心 C.数 D.学
4.如图,,是内任意一条射线,,分别平分,,下列结论错误的是( )
A. B.
C. D.
5.如图,点是直线上一点,平分,,则以下结论:①与互为余角;②;③;④若,则.其中正确的是( )
A.只有①④ B.只有③④ C.只有①③④ D.①②③④
6.下列说法:有理数可以分为正有理数和负有理数;若,则为负数;的二次项系数是;所有的有理数都可以用数轴上的点来表示;五棱柱有个面,条棱.其中正确的个数是( )
A.个 B.个 C.个 D.个
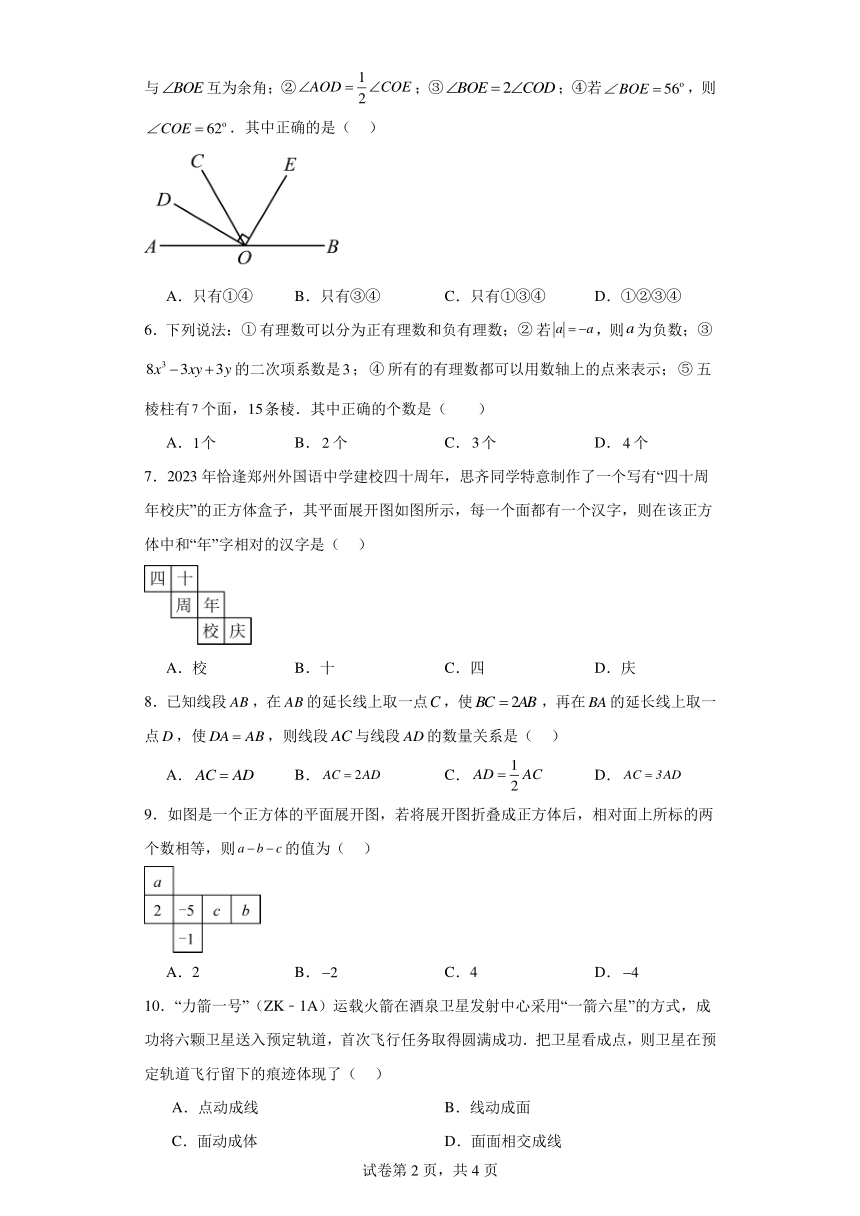
7.2023年恰逢郑州外国语中学建校四十周年,思齐同学特意制作了一个写有“四十周年校庆”的正方体盒子,其平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“年”字相对的汉字是( )
A.校 B.十 C.四 D.庆
8.已知线段,在的延长线上取一点,使,再在的延长线上取一点,使,则线段与线段的数量关系是( )
A. B. C. D.
9.如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则的值为( )
A.2 B. C.4 D.
10.“力箭一号”(ZK﹣1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,首次飞行任务取得圆满成功.把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交成线
评卷人得分
二、填空题
11.在直线l上取A、B、C三点,使得,.如果O是线段的中点,则线段的长度为 cm.
12.如图,C是线段上一点,给出下列表达式:①;②;③;④,其中,能表示C是线段中点的式子有 .(只填所有符合条件的序号).
13.已知,从点O引射线,,若,则 .
14.如图,正方体的平面展开图,每个正方形中都标注了一个汉字.反向思考,正方体中,标注“锦”的面的对面标注的汉字是 .
15.开学整理教室时,卫生委员总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌就摆在一条线上,整整齐齐,其运用的数学原理是 .
16.如图,,,平分,则 .
评卷人得分
三、问答题
17.如图,已知点为线段上一点,,,、分别是、的中点.求:
(1)求的长度;
(2)求的长度;
(3)若在直线上,且,求的长度.
18.如图,O是直线上一点,OD平分,.
(1)若,求的度数;
(2)若,则______(用含的代数式表示).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了线段的和差运算,根据线段中点的定义与线段的和差结合图形逐一进行分析即可.能够利用中点的性质及线段的和差关系求解一些线段之间的关系是解本题的关键.
【详解】解:如图, ∵M、N分别是线段、的中点,
∴,,
∵,
∴,
∴,
∴,
∴,即,故①符合题意;
∵,
∴,
∴,
∴,故②符合题意;
∵,
∴,
故③符合题意;
∵,,
∴,
∵,,
∴
,
故④不符合题意,
故选:A.
2.C
【分析】本题考查单项式,多项式,角.根据单项式:“数字与字母的乘积,单个数字和字母也是单项式”,多项式的次数:“最高项的次数”,常数项:“不含字母的项”,有公共端点的两条射线组成角,逐一进行判断即可.
【详解】解:x是单项式;故(1)正确;
多项式的次数是4;故(2)正确;
的常数项是;故(3)错误;
有公共端点的两条射线组成的图形叫做角;故(4)错误;
故选C.
3.B
【分析】本题考查了正方体的展开图得知识,正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】正方体的表面展开图,相对的面之间一定相隔一个正方形,
“数”与“养”是相对面,
“学”与“核”是相对面,
“素”与“心”是相对面,
故选:B.
4.D
【分析】考查角平分线的定义、互为余角的意义,根据角平分线的定义,互余的意义和等量代换,逐个结论进行判断即可得出答案.
【详解】解:∵,分别平分,,
∴,
∴,
即:,因此A正确,不符合题意;
,因此B正确,不符合题意;
∵,
∴,因此C正确,不符合题意;
∵是内任意一条射线,
∴ 不一定会等于,即 不一定会等于,因此D不正确,符合题意;
故选:D.
5.C
【分析】本题主要考查角平分线、余角与补角,根据补角以及角平分线的定义解决此题.
【详解】解:,
,
与互为余角,故①正确.
平分,
,无法推断得到,故②错误.
设,
,
,
平分,
,则,
,
,即,故③正确.
,
.
平分,
,故④正确.
综上:正确的有①③④.
故选:C.
6.B
【分析】本题考查了有理数、数轴、绝对值、多项式以及棱柱,根据有理数、数轴、绝对值、多项式以及棱柱的形体特征逐项进行判断即可,掌握有理数、数轴、绝对值、多项式的定义以及棱柱的形体特征是解题的关键.
【详解】解:有理数可以分为正有理数,,负有理数,故错误;
若,则,因此不正确;
多项式的二次项系数是,因此不正确;
所有的有理数都可以用数轴上的点来表示,因此正确;
五棱柱有个面,15条棱.因此正确;
综上所述,正确的有,
故选:.
7.C
【分析】本题考查正方体展开图的相对面.根据正方体表面展开图的“相间、Z端是对面”,进行判断即可.
【详解】解:根据正方体表面展开图的“相间、Z端是对面”可知,
“年”与“四”是对面,
故选:C.
8.D
【分析】本题考查了线段的画图和有关计算,属于基础题型,解题的关键是根据题意画出图形,得出相关线段之间的关系.
【详解】解:依据题意画出下图:
由图可知:,
,,
,
即.
故选:D.
9.A
【分析】本题考查正方体展开图的相对面,代数式求值.根据正方体表面展开图的“相间、Z端是对面”,确定的值,再代值计算即可.
【详解】解:由图可知:,
∴;
故选A.
10.A
【分析】本题考查点,线,面,体之间的关系,根据题意,卫星看成点,故体现了点动成线,即可.
【详解】解:由题意,得:把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了点动成线;
故选A.
11.或
【分析】本题考查了与线段中点有关的计算问题,根据题意,画出图形进行分类讨论是解题关键.
【详解】解:①如图所示:
∵,.
∴,
∵O是线段的中点,
∴,
∴.
②如图所示:
∵,.
∴,
∵O是线段的中点,
∴,
∴,
综上所述:或,
故答案为:或.
12.①②③
【分析】本题考查了线段的中点即把线段分成相等的两条线段的点,线段的和与差,熟练掌握线段中点的意义,灵活运用线段的和差是解题的关键.
【详解】时,点C是线段中点,
故①正确;
时,点C是线段中点,
故②正确;
时,点C是线段中点,
故③正确;
时,点C不一定是线段中点,
故④错误,
故答案为:①②③.
13.或或
【分析】本题考查的是角的和差倍分,先分情况画图,再求解是解本题的关键,本题分三种情况画图,射线, 都在的外部,或内部,或一条在内部,一条在外部,再求解即可.
【详解】解:∵,
∴,
如图,
∴,
如图,
∴,
如图,
∴;
综上:为或或.
故答案为:或或
14.祝
【分析】本题考查了正方体相对两个面上的文字,根据正方体表面展开图的特征即可求解,掌握正方体表面展开图形的“相间、端是对面”是解题的关键.
【详解】解:根据正方体表面展开图形的“相间、端是对面”可知,
“锦”与“祝”相对,
故答案为:祝.
15.两点确定一条直线
【分析】本题考查了两点确定一条直线.熟练掌握两点确定一条直线是解题的关键.
根据两点确定一条直线进行作答即可.
【详解】解:由题意知,运用的数学原理是两点确定一条直线,
故答案为:两点确定一条直线.
16./度
【分析】本题考查了角的计算和角平分线定义,根据已知可求得的度数,由角平分线的定义求出的度数即可.
【详解】解:,,
,
平分,
.
故答案为:.
17.(1)
(2);
(3)或.
【分析】()直接根据是的中点可得答案;
()先求出的长,然后根据是的中点求出,即为的长;
()分在点的右侧、在点的左侧两种情况进行计算即可;
本题考查了关于线段的中点的计算,线段的和与差的计算,读懂题意熟练运用线段的和差倍分是解题的关键.
【详解】(1)由线段中点的性质,;
(2)由线段的和差,得,
由线段中点的性质,得,
由线段的和差,得;
(3)当在点的右侧时,,
当在点的左侧时,,
∴的长度为或.
18.(1)
(2)
【分析】本题考查了有关角的计算;
(1)求出,根据平分得出,求出,根据求出即可;
(2)求出,根据平分得出,求出,根据求出即可.
【详解】(1)是直线上一点,
,
,
,
平分,
,
,,
;
(2)是直线上一点,
,
,
,
平分,
,
,,
.
故答案为:.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,C、D是线段上两点,M、N分别是线段、的中点,下列结论:①若,则;②若,则;③;④.其中正确的结论是( )
A.①②③ B.③④ C.①②④ D.①②③④
2.下列说法中:(1)x是单项式;(2)多项式的次数是4;(3)的常数项是1;(4)由两条射线组成的图形叫做角,正确的个数是( )
A.0个 B.1个 C.2个 D.3个
3.如图是一个正方体盒子展开后的平面图形,六个面上分别写有“数”、“学”、“核”“心”、“素”、“养”,则“素”字对面的字是( )
A.核 B.心 C.数 D.学
4.如图,,是内任意一条射线,,分别平分,,下列结论错误的是( )
A. B.
C. D.
5.如图,点是直线上一点,平分,,则以下结论:①与互为余角;②;③;④若,则.其中正确的是( )
A.只有①④ B.只有③④ C.只有①③④ D.①②③④
6.下列说法:有理数可以分为正有理数和负有理数;若,则为负数;的二次项系数是;所有的有理数都可以用数轴上的点来表示;五棱柱有个面,条棱.其中正确的个数是( )
A.个 B.个 C.个 D.个
7.2023年恰逢郑州外国语中学建校四十周年,思齐同学特意制作了一个写有“四十周年校庆”的正方体盒子,其平面展开图如图所示,每一个面都有一个汉字,则在该正方体中和“年”字相对的汉字是( )
A.校 B.十 C.四 D.庆
8.已知线段,在的延长线上取一点,使,再在的延长线上取一点,使,则线段与线段的数量关系是( )
A. B. C. D.
9.如图是一个正方体的平面展开图,若将展开图折叠成正方体后,相对面上所标的两个数相等,则的值为( )
A.2 B. C.4 D.
10.“力箭一号”(ZK﹣1A)运载火箭在酒泉卫星发射中心采用“一箭六星”的方式,成功将六颗卫星送入预定轨道,首次飞行任务取得圆满成功.把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了( )
A.点动成线 B.线动成面
C.面动成体 D.面面相交成线
评卷人得分
二、填空题
11.在直线l上取A、B、C三点,使得,.如果O是线段的中点,则线段的长度为 cm.
12.如图,C是线段上一点,给出下列表达式:①;②;③;④,其中,能表示C是线段中点的式子有 .(只填所有符合条件的序号).
13.已知,从点O引射线,,若,则 .
14.如图,正方体的平面展开图,每个正方形中都标注了一个汉字.反向思考,正方体中,标注“锦”的面的对面标注的汉字是 .
15.开学整理教室时,卫生委员总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌就摆在一条线上,整整齐齐,其运用的数学原理是 .
16.如图,,,平分,则 .
评卷人得分
三、问答题
17.如图,已知点为线段上一点,,,、分别是、的中点.求:
(1)求的长度;
(2)求的长度;
(3)若在直线上,且,求的长度.
18.如图,O是直线上一点,OD平分,.
(1)若,求的度数;
(2)若,则______(用含的代数式表示).
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【分析】本题考查了线段的和差运算,根据线段中点的定义与线段的和差结合图形逐一进行分析即可.能够利用中点的性质及线段的和差关系求解一些线段之间的关系是解本题的关键.
【详解】解:如图, ∵M、N分别是线段、的中点,
∴,,
∵,
∴,
∴,
∴,
∴,即,故①符合题意;
∵,
∴,
∴,
∴,故②符合题意;
∵,
∴,
故③符合题意;
∵,,
∴,
∵,,
∴
,
故④不符合题意,
故选:A.
2.C
【分析】本题考查单项式,多项式,角.根据单项式:“数字与字母的乘积,单个数字和字母也是单项式”,多项式的次数:“最高项的次数”,常数项:“不含字母的项”,有公共端点的两条射线组成角,逐一进行判断即可.
【详解】解:x是单项式;故(1)正确;
多项式的次数是4;故(2)正确;
的常数项是;故(3)错误;
有公共端点的两条射线组成的图形叫做角;故(4)错误;
故选C.
3.B
【分析】本题考查了正方体的展开图得知识,正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【详解】正方体的表面展开图,相对的面之间一定相隔一个正方形,
“数”与“养”是相对面,
“学”与“核”是相对面,
“素”与“心”是相对面,
故选:B.
4.D
【分析】考查角平分线的定义、互为余角的意义,根据角平分线的定义,互余的意义和等量代换,逐个结论进行判断即可得出答案.
【详解】解:∵,分别平分,,
∴,
∴,
即:,因此A正确,不符合题意;
,因此B正确,不符合题意;
∵,
∴,因此C正确,不符合题意;
∵是内任意一条射线,
∴ 不一定会等于,即 不一定会等于,因此D不正确,符合题意;
故选:D.
5.C
【分析】本题主要考查角平分线、余角与补角,根据补角以及角平分线的定义解决此题.
【详解】解:,
,
与互为余角,故①正确.
平分,
,无法推断得到,故②错误.
设,
,
,
平分,
,则,
,
,即,故③正确.
,
.
平分,
,故④正确.
综上:正确的有①③④.
故选:C.
6.B
【分析】本题考查了有理数、数轴、绝对值、多项式以及棱柱,根据有理数、数轴、绝对值、多项式以及棱柱的形体特征逐项进行判断即可,掌握有理数、数轴、绝对值、多项式的定义以及棱柱的形体特征是解题的关键.
【详解】解:有理数可以分为正有理数,,负有理数,故错误;
若,则,因此不正确;
多项式的二次项系数是,因此不正确;
所有的有理数都可以用数轴上的点来表示,因此正确;
五棱柱有个面,15条棱.因此正确;
综上所述,正确的有,
故选:.
7.C
【分析】本题考查正方体展开图的相对面.根据正方体表面展开图的“相间、Z端是对面”,进行判断即可.
【详解】解:根据正方体表面展开图的“相间、Z端是对面”可知,
“年”与“四”是对面,
故选:C.
8.D
【分析】本题考查了线段的画图和有关计算,属于基础题型,解题的关键是根据题意画出图形,得出相关线段之间的关系.
【详解】解:依据题意画出下图:
由图可知:,
,,
,
即.
故选:D.
9.A
【分析】本题考查正方体展开图的相对面,代数式求值.根据正方体表面展开图的“相间、Z端是对面”,确定的值,再代值计算即可.
【详解】解:由图可知:,
∴;
故选A.
10.A
【分析】本题考查点,线,面,体之间的关系,根据题意,卫星看成点,故体现了点动成线,即可.
【详解】解:由题意,得:把卫星看成点,则卫星在预定轨道飞行留下的痕迹体现了点动成线;
故选A.
11.或
【分析】本题考查了与线段中点有关的计算问题,根据题意,画出图形进行分类讨论是解题关键.
【详解】解:①如图所示:
∵,.
∴,
∵O是线段的中点,
∴,
∴.
②如图所示:
∵,.
∴,
∵O是线段的中点,
∴,
∴,
综上所述:或,
故答案为:或.
12.①②③
【分析】本题考查了线段的中点即把线段分成相等的两条线段的点,线段的和与差,熟练掌握线段中点的意义,灵活运用线段的和差是解题的关键.
【详解】时,点C是线段中点,
故①正确;
时,点C是线段中点,
故②正确;
时,点C是线段中点,
故③正确;
时,点C不一定是线段中点,
故④错误,
故答案为:①②③.
13.或或
【分析】本题考查的是角的和差倍分,先分情况画图,再求解是解本题的关键,本题分三种情况画图,射线, 都在的外部,或内部,或一条在内部,一条在外部,再求解即可.
【详解】解:∵,
∴,
如图,
∴,
如图,
∴,
如图,
∴;
综上:为或或.
故答案为:或或
14.祝
【分析】本题考查了正方体相对两个面上的文字,根据正方体表面展开图的特征即可求解,掌握正方体表面展开图形的“相间、端是对面”是解题的关键.
【详解】解:根据正方体表面展开图形的“相间、端是对面”可知,
“锦”与“祝”相对,
故答案为:祝.
15.两点确定一条直线
【分析】本题考查了两点确定一条直线.熟练掌握两点确定一条直线是解题的关键.
根据两点确定一条直线进行作答即可.
【详解】解:由题意知,运用的数学原理是两点确定一条直线,
故答案为:两点确定一条直线.
16./度
【分析】本题考查了角的计算和角平分线定义,根据已知可求得的度数,由角平分线的定义求出的度数即可.
【详解】解:,,
,
平分,
.
故答案为:.
17.(1)
(2);
(3)或.
【分析】()直接根据是的中点可得答案;
()先求出的长,然后根据是的中点求出,即为的长;
()分在点的右侧、在点的左侧两种情况进行计算即可;
本题考查了关于线段的中点的计算,线段的和与差的计算,读懂题意熟练运用线段的和差倍分是解题的关键.
【详解】(1)由线段中点的性质,;
(2)由线段的和差,得,
由线段中点的性质,得,
由线段的和差,得;
(3)当在点的右侧时,,
当在点的左侧时,,
∴的长度为或.
18.(1)
(2)
【分析】本题考查了有关角的计算;
(1)求出,根据平分得出,求出,根据求出即可;
(2)求出,根据平分得出,求出,根据求出即可.
【详解】(1)是直线上一点,
,
,
,
平分,
,
,,
;
(2)是直线上一点,
,
,
,
平分,
,
,,
.
故答案为:.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
