2023-2024学年沪科版(2012)七年级下册第十章相交线平行线与平移单元测试卷(含答案)
文档属性
| 名称 | 2023-2024学年沪科版(2012)七年级下册第十章相交线平行线与平移单元测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 718.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览

文档简介
2023-2024学年 沪科版(2012)七年级下册 第十章 相交线 平行线与平移 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
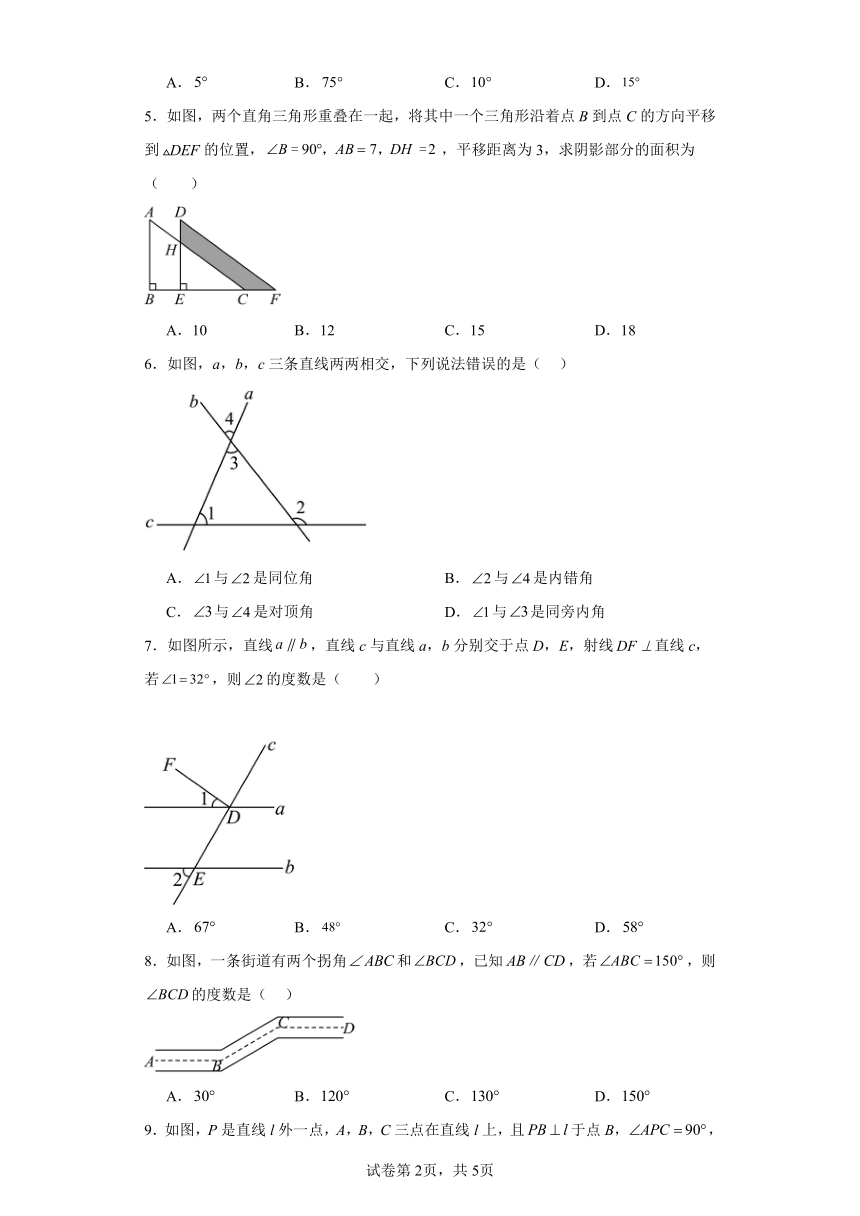
1.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
2.如图,直线,直线l分别与相交,若,则( )
A. B. C. D.
3.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
4.如图,,平分,则等于( )
A. B. C. D.
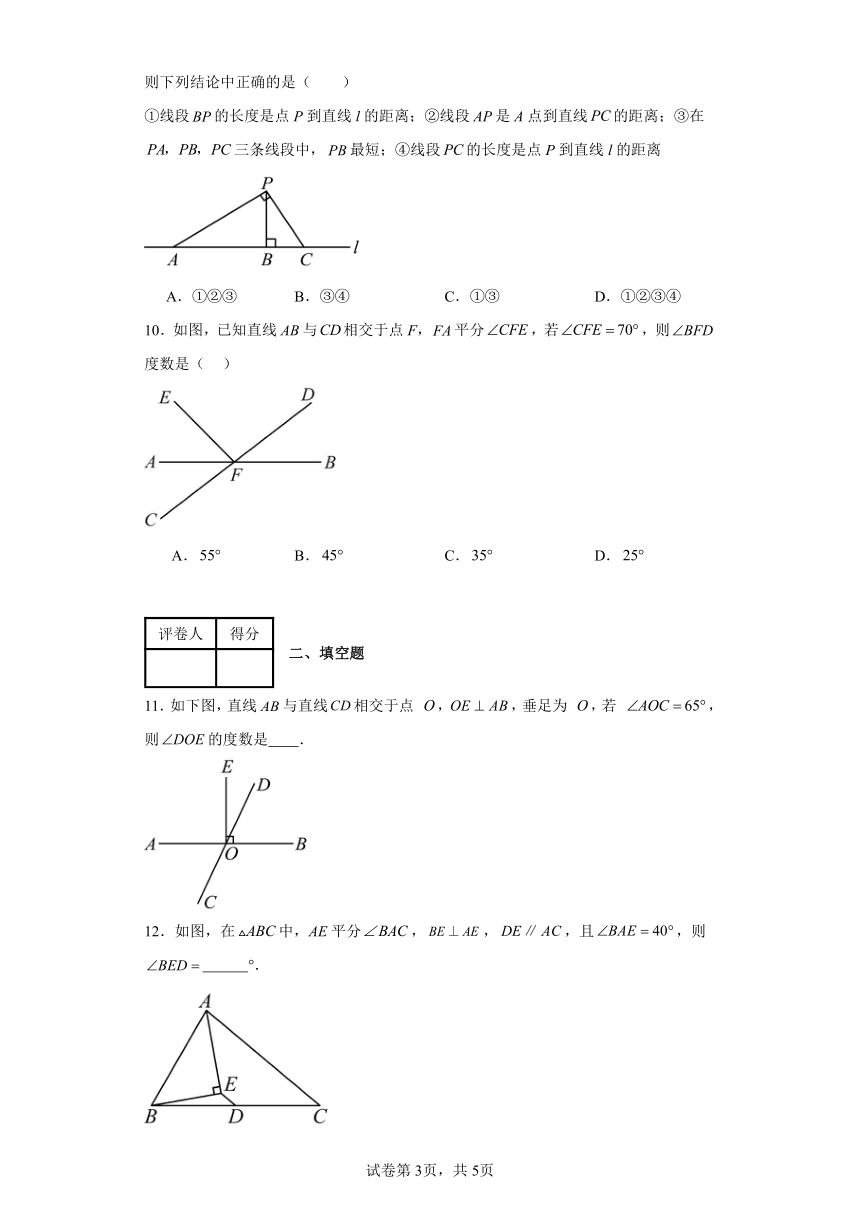
5.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置,,平移距离为3,求阴影部分的面积为( )
A.10 B.12 C.15 D.18
6.如图,a,b,c三条直线两两相交,下列说法错误的是( )
A.与是同位角 B.与是内错角
C.与是对顶角 D.与是同旁内角
7.如图所示,直线,直线c与直线a,b分别交于点D,E,射线直线c,若,则的度数是( )
A. B. C. D.
8.如图,一条街道有两个拐角和,已知,若,则的度数是( )
A. B. C. D.
9.如图,P是直线l外一点,A,B,C三点在直线l上,且于点B,,则下列结论中正确的是( )
①线段的长度是点P到直线l的距离;②线段是A点到直线的距离;③在三条线段中,最短;④线段的长度是点P到直线l的距离
A.①②③ B.③④ C.①③ D.①②③④
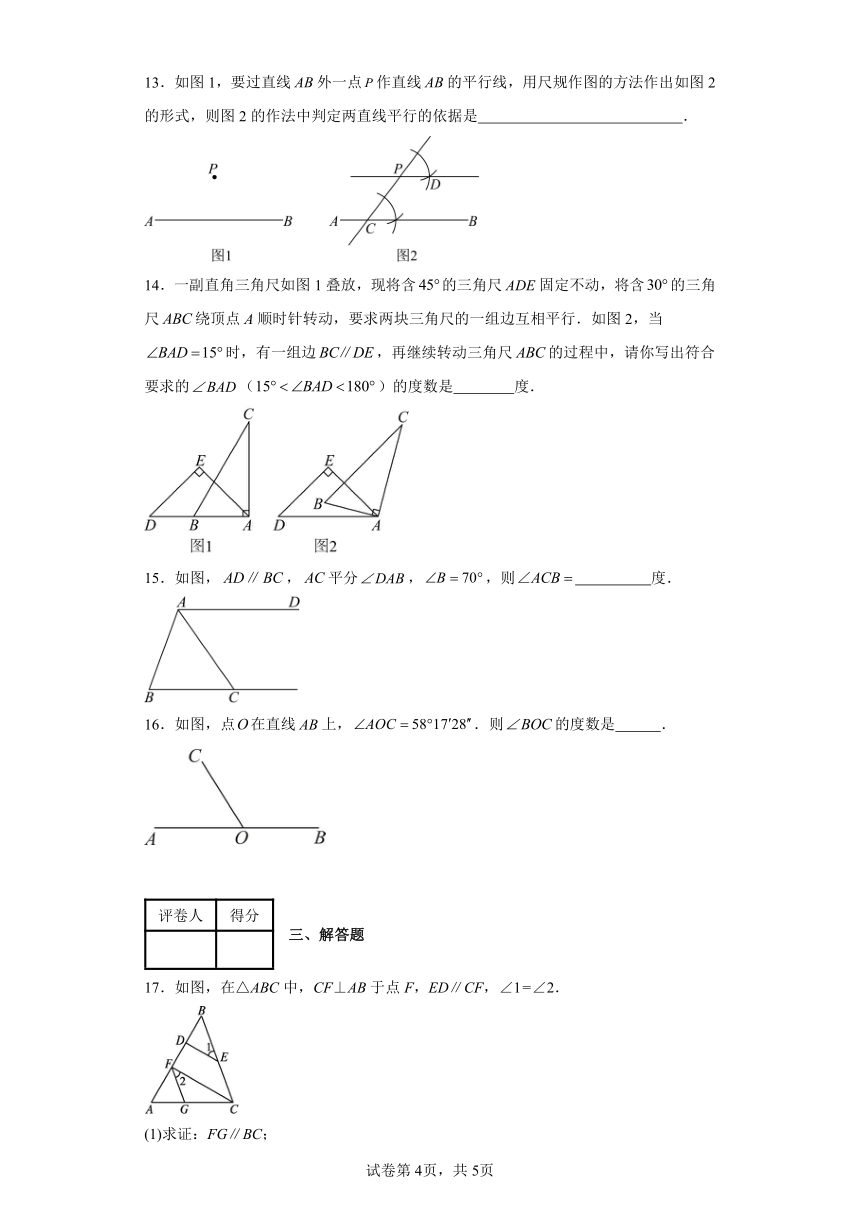
10.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
评卷人得分
二、填空题
11.如下图,直线与直线相交于点 ,,垂足为 ,若 ,则的度数是 .
12.如图,在中,AE平分,,,且,则 °.
13.如图1,要过直线外一点作直线的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 .
14.一副直角三角尺如图1叠放,现将含的三角尺固定不动,将含的三角尺绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图2,当时,有一组边,再继续转动三角尺的过程中,请你写出符合要求的()的度数是 度.
15.如图,,平分,,则 度.
16.如图,点在直线上,.则的度数是 .
评卷人得分
三、解答题
17.如图,在△ABC中,CF⊥AB于点F,ED∥CF,∠1=∠2.
(1)求证:FG∥BC;
(2)若∠A=60°,∠AGF=70°,求∠B及∠2的度数.
评卷人得分
四、证明题
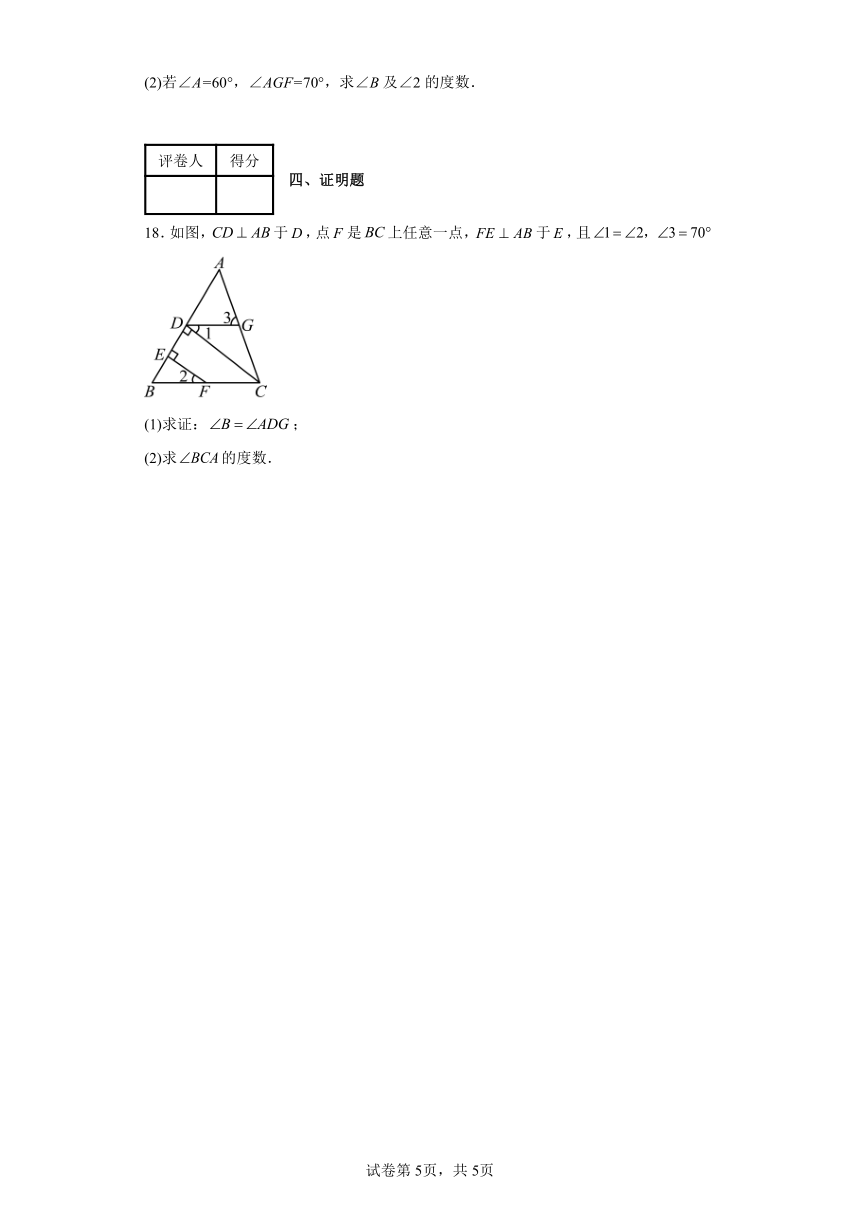
18.如图,于,点是上任意一点,于,且
(1)求证:;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了平行线的判定,正确识别三线八角中的同位角、内错角、同旁内角是解答本题的关键.
只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,利用平行线的判定定理,逐一判断,得出结论.
【详解】解:选项中,因为,所以(同位角相等,两直线平行),故本选项不符合题意.
选项中,因为,所以(同旁内角互补,两直线平行),故本选项不符合题意.
选项中,因为,所以(内错角相等,两直线平行),故本选项不符合题意.
选项中,因为,所以(同位角相等,两直线平行),不能证出,故本选项符合题意.
故选:.
2.C
【分析】本题考查了平行线性质和对顶角性质,关键是求出和得出.设与直线l交于点,与直线l交于点,先求出,根据平行线性质求出,代入即可求出答案.
【详解】解:设与直线l交于点,与直线l交于点,
∵,
∵,
∴,
∴,
故选:C.
3.B
【分析】此题主要考查了平行线的判定,根据平行线的判定定理同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行分别进行分析.关键是掌握平行线的判定定理.
【详解】解:,
,故选项A不合题意;
,
,不能判定,故选项B符合题意;
,
,故选项C不合题意;
∵,
,故选项D不合题意.
故选:B.
4.A
【分析】本题考查平行线的性质,根据平行线的性质得到,求出,再利用角平分线计算即可.
【详解】∵,
∴,
∴,
∴,
∵平分,
∴,
∴,
故选:A.
5.D
【分析】本题考查了平移的基本性质,掌握①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等是解题的关键.由,推出即可解决问题.
【详解】解:平移距离为3,
,
,
,
,
,
∴阴影部分的面积为.
故选:D.
6.B
【分析】本题考查相交直线所成相关角的概念,解答关键是熟知同位角、内错角、同旁内角、对顶角的相关概念和判断方法.
【详解】解:A.与是直线a、直线b被直线c所截,所得到的同位角,因此选项A不符合题意;
B.与是直线a、直线c被直线b所截,所得到的同位角,因此选项B符合题意;
C.与是对顶角,因此选项C不符合题意;
D.与是直线b、直线c被直线a所截,所得到的同旁内角,因此选项D不符合题意;
故选:B.
7.D
【分析】本题主要考查了平行线的性质,由平行线的性质可得:,由垂直的定义可求出的度数,即可求得.熟记平行线的性质是解决问题的关键.
【详解】解:∵,
∴,
∵直线c,
∴,
∵,
∴,
∴.
故选:D.
8.D
【分析】本题考查了平行线的性质:两直线平行,内错角相等,由,根据两直线平行,内错角相等,可得的度数,解题的关键是将实际问题转化为数学问题求解.
【详解】∵
∴(两直线平行,内错角相等).
故选:D.
9.C
【分析】本题考查了点到直线的距离及垂线段最短等知识点.点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离.熟记相关结论是解题关键.
【详解】解:∵于点B,
∴线段的长度是点P到直线l的距离,故①正确,④错误;
∵,
∴线段的长度是A点到直线的距离,故②错误;
根据垂线段最短,在三条线段中,最短,故③正确;
故选:C.
10.C
【分析】本题考查了角平分线的定义及对顶角相等等知识点.先根据角平分线的定义得出,再根据对顶角相等即可得出答案.
【详解】解:∵平分,
∴,
∴.
故选:C.
11./25度
【分析】本题考查垂直的定义,对顶角的性质,根据垂直可得,根据对顶角相等可得,则.
【详解】解:,
,
,
,
,
故答案为:.
12.
【分析】已知平分,,根据两直线平行同旁内角互补,可求得的度数,再由垂直的定义求出,再由周角为,求得度数.此题考查了平行线的性质和角平分线定义,解题的关键是熟练掌握平行线的性质及其应用.
【详解】∵平分,
∴,
∵,
∴,
∴,
∵,
∴
∵,
∴,
故答案为: .
13.同位角相等,两直线平行
【分析】本题考查作图—复杂作图,平行线的判定等知识,解题的关键是读懂图像信息,掌握平行线的判定.根据同位角相等两直线平行,判断即可.
【详解】解:由作图可知:,
∴(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
14.或或
【分析】本题考查的是平行线的判定与性质,根据题意画出图形,再由平行线的判定定理即可得出结论.
【详解】解:当时,;
当时,
∵,
∴;
当时,
∵,
∴.
综上所述,的度数为或或;
故答案为:或或.
15.55
【分析】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
根据平行线的性质定理得出,根据角平分线的定义得到,再根据平行线的性质求解即可.
【详解】解:∵,
平分,
故答案为:55.
16.
【分析】本题主要考查了邻补角的定义.掌握邻补角的定义:“如果两个角互为邻补角,那么它们的和为”是解题的关键.
【详解】解:∵点O在直线AB上,且,
∴,
故答案为:.
17.(1)见解析
(2)∠B=50°,∠2=40°
【详解】(1)证明 ∵DE∥FC,
∴∠1=∠BCF.
又∵∠1=∠2,∴∠2=∠BCF,
∴FG∥BC.
(2)解 ∵在△AFG中,∠A=60°,∠AGF=70°,
∴∠AFG=180°-∠A-∠AGF=50°.
又由(1)知,FG∥BC,
∴∠B=∠AFG=50°.
∵CF⊥AB,DE∥FC,∴ED⊥AB,
∴∠1=90°-∠B=40°,
∴∠2=40°.
18.(1)见详解
(2)
【分析】本题考查了平行线的判定和性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
(1)由,则,则,从而证得,即;
(2)由,即可得到.
【详解】(1)∵,
(2)∵,
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
2.如图,直线,直线l分别与相交,若,则( )
A. B. C. D.
3.如图,点E在的延长线上,下列条件中不能判定的是( )
A. B. C. D.
4.如图,,平分,则等于( )
A. B. C. D.
5.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置,,平移距离为3,求阴影部分的面积为( )
A.10 B.12 C.15 D.18
6.如图,a,b,c三条直线两两相交,下列说法错误的是( )
A.与是同位角 B.与是内错角
C.与是对顶角 D.与是同旁内角
7.如图所示,直线,直线c与直线a,b分别交于点D,E,射线直线c,若,则的度数是( )
A. B. C. D.
8.如图,一条街道有两个拐角和,已知,若,则的度数是( )
A. B. C. D.
9.如图,P是直线l外一点,A,B,C三点在直线l上,且于点B,,则下列结论中正确的是( )
①线段的长度是点P到直线l的距离;②线段是A点到直线的距离;③在三条线段中,最短;④线段的长度是点P到直线l的距离
A.①②③ B.③④ C.①③ D.①②③④
10.如图,已知直线与相交于点F,平分,若,则度数是( )
A. B. C. D.
评卷人得分
二、填空题
11.如下图,直线与直线相交于点 ,,垂足为 ,若 ,则的度数是 .
12.如图,在中,AE平分,,,且,则 °.
13.如图1,要过直线外一点作直线的平行线,用尺规作图的方法作出如图2的形式,则图2的作法中判定两直线平行的依据是 .
14.一副直角三角尺如图1叠放,现将含的三角尺固定不动,将含的三角尺绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图2,当时,有一组边,再继续转动三角尺的过程中,请你写出符合要求的()的度数是 度.
15.如图,,平分,,则 度.
16.如图,点在直线上,.则的度数是 .
评卷人得分
三、解答题
17.如图,在△ABC中,CF⊥AB于点F,ED∥CF,∠1=∠2.
(1)求证:FG∥BC;
(2)若∠A=60°,∠AGF=70°,求∠B及∠2的度数.
评卷人得分
四、证明题
18.如图,于,点是上任意一点,于,且
(1)求证:;
(2)求的度数.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了平行线的判定,正确识别三线八角中的同位角、内错角、同旁内角是解答本题的关键.
只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行,利用平行线的判定定理,逐一判断,得出结论.
【详解】解:选项中,因为,所以(同位角相等,两直线平行),故本选项不符合题意.
选项中,因为,所以(同旁内角互补,两直线平行),故本选项不符合题意.
选项中,因为,所以(内错角相等,两直线平行),故本选项不符合题意.
选项中,因为,所以(同位角相等,两直线平行),不能证出,故本选项符合题意.
故选:.
2.C
【分析】本题考查了平行线性质和对顶角性质,关键是求出和得出.设与直线l交于点,与直线l交于点,先求出,根据平行线性质求出,代入即可求出答案.
【详解】解:设与直线l交于点,与直线l交于点,
∵,
∵,
∴,
∴,
故选:C.
3.B
【分析】此题主要考查了平行线的判定,根据平行线的判定定理同位角相等,两直线平行.内错角相等,两直线平行.同旁内角互补,两直线平行分别进行分析.关键是掌握平行线的判定定理.
【详解】解:,
,故选项A不合题意;
,
,不能判定,故选项B符合题意;
,
,故选项C不合题意;
∵,
,故选项D不合题意.
故选:B.
4.A
【分析】本题考查平行线的性质,根据平行线的性质得到,求出,再利用角平分线计算即可.
【详解】∵,
∴,
∴,
∴,
∵平分,
∴,
∴,
故选:A.
5.D
【分析】本题考查了平移的基本性质,掌握①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等是解题的关键.由,推出即可解决问题.
【详解】解:平移距离为3,
,
,
,
,
,
∴阴影部分的面积为.
故选:D.
6.B
【分析】本题考查相交直线所成相关角的概念,解答关键是熟知同位角、内错角、同旁内角、对顶角的相关概念和判断方法.
【详解】解:A.与是直线a、直线b被直线c所截,所得到的同位角,因此选项A不符合题意;
B.与是直线a、直线c被直线b所截,所得到的同位角,因此选项B符合题意;
C.与是对顶角,因此选项C不符合题意;
D.与是直线b、直线c被直线a所截,所得到的同旁内角,因此选项D不符合题意;
故选:B.
7.D
【分析】本题主要考查了平行线的性质,由平行线的性质可得:,由垂直的定义可求出的度数,即可求得.熟记平行线的性质是解决问题的关键.
【详解】解:∵,
∴,
∵直线c,
∴,
∵,
∴,
∴.
故选:D.
8.D
【分析】本题考查了平行线的性质:两直线平行,内错角相等,由,根据两直线平行,内错角相等,可得的度数,解题的关键是将实际问题转化为数学问题求解.
【详解】∵
∴(两直线平行,内错角相等).
故选:D.
9.C
【分析】本题考查了点到直线的距离及垂线段最短等知识点.点到直线的距离,即过这一点做目标直线的垂线,由这一点至垂足的距离.熟记相关结论是解题关键.
【详解】解:∵于点B,
∴线段的长度是点P到直线l的距离,故①正确,④错误;
∵,
∴线段的长度是A点到直线的距离,故②错误;
根据垂线段最短,在三条线段中,最短,故③正确;
故选:C.
10.C
【分析】本题考查了角平分线的定义及对顶角相等等知识点.先根据角平分线的定义得出,再根据对顶角相等即可得出答案.
【详解】解:∵平分,
∴,
∴.
故选:C.
11./25度
【分析】本题考查垂直的定义,对顶角的性质,根据垂直可得,根据对顶角相等可得,则.
【详解】解:,
,
,
,
,
故答案为:.
12.
【分析】已知平分,,根据两直线平行同旁内角互补,可求得的度数,再由垂直的定义求出,再由周角为,求得度数.此题考查了平行线的性质和角平分线定义,解题的关键是熟练掌握平行线的性质及其应用.
【详解】∵平分,
∴,
∵,
∴,
∴,
∵,
∴
∵,
∴,
故答案为: .
13.同位角相等,两直线平行
【分析】本题考查作图—复杂作图,平行线的判定等知识,解题的关键是读懂图像信息,掌握平行线的判定.根据同位角相等两直线平行,判断即可.
【详解】解:由作图可知:,
∴(同位角相等,两直线平行),
故答案为:同位角相等,两直线平行.
14.或或
【分析】本题考查的是平行线的判定与性质,根据题意画出图形,再由平行线的判定定理即可得出结论.
【详解】解:当时,;
当时,
∵,
∴;
当时,
∵,
∴.
综上所述,的度数为或或;
故答案为:或或.
15.55
【分析】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
根据平行线的性质定理得出,根据角平分线的定义得到,再根据平行线的性质求解即可.
【详解】解:∵,
平分,
故答案为:55.
16.
【分析】本题主要考查了邻补角的定义.掌握邻补角的定义:“如果两个角互为邻补角,那么它们的和为”是解题的关键.
【详解】解:∵点O在直线AB上,且,
∴,
故答案为:.
17.(1)见解析
(2)∠B=50°,∠2=40°
【详解】(1)证明 ∵DE∥FC,
∴∠1=∠BCF.
又∵∠1=∠2,∴∠2=∠BCF,
∴FG∥BC.
(2)解 ∵在△AFG中,∠A=60°,∠AGF=70°,
∴∠AFG=180°-∠A-∠AGF=50°.
又由(1)知,FG∥BC,
∴∠B=∠AFG=50°.
∵CF⊥AB,DE∥FC,∴ED⊥AB,
∴∠1=90°-∠B=40°,
∴∠2=40°.
18.(1)见详解
(2)
【分析】本题考查了平行线的判定和性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.
(1)由,则,则,从而证得,即;
(2)由,即可得到.
【详解】(1)∵,
(2)∵,
答案第1页,共2页
答案第1页,共2页
