1.7 近似数课件(共14张PPT) 沪科版七年级数学上册
文档属性
| 名称 | 1.7 近似数课件(共14张PPT) 沪科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:16:58 | ||
图片预览






文档简介
(共14张PPT)
1.7 近似数
第1章 有理数
1.理解准确数、近似数的概念,并能辨别它们.
2.会用四舍五入法按要求取一个数的近似数,能说出一个近似数精确到的位数.
活动1:请同学们结合实际,回答下列问题.
(1)我们班有多少名同学,其中男生多少名,女生多少名?
(2)七年级上册数学课本有多少页?
(3)你的身高是多少?
(4)七年级上册数学课本有多宽?
任务一:能辨别准确数与近似数
与实际完全符合的数叫做准确数;
与实际数值很接近的数叫做近似数.
这些数据中,哪些数是与实际完全符合的?哪些数是与实际接近呢?
活动2:说出语句中的准确数和近似数,并和同伴交流数的辨别方法.
1.妈妈去买水果,买了8个苹果,大约3千克.
2.小民与小李买了2瓶水,4根黄瓜,6袋香巴拉牛肉干,约20元,然后骑车去3.5km外去郊游,大约玩了4.5小时回家.
3.我国共有56个民族.
4.举世瞩目的西气东输工程全长4000km.
近似数是由测量、称量、估计等等得到的数.近似数一般带有大约、左右、大概等等词语.
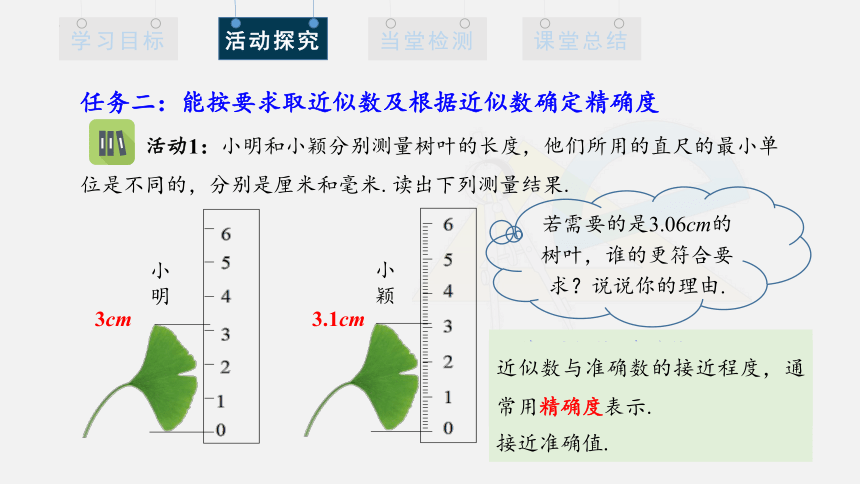
活动1:小明和小颖分别测量树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.读出下列测量结果.
任务二:能按要求取近似数及根据近似数确定精确度
小颖
小明
3cm
3.1cm
若需要的是3.06cm的树叶,谁的更符合要求?说说你的理由.
误差=近似值-准确值.
误差可能是正数,也可能是负数,误差的绝对值越小,近似值就越接近准确值.
近似数与准确数的接近程度,通常用精确度表示.
仿写:按四舍五入法对圆周率π取近似数时,有
π≈3 (精确到个位)
π≈3.1 (精确到0.1或叫做精确到十分位)
π≈3.14 (精确到0.01或叫做精确到百分位)
π≈3.142 (精确到 或叫做精确到 )
π≈3.141 6 (精确到 或叫做精确到 )
……
0.001
千分位
0.0001
万分位
1 0.1 十分位
4 0.01 百分位
2
6
小组讨论:观察上述近似数说说怎么确定一个近似数的精确度?那又是怎么取一个数的近似数?
活动小结
1.确定近似数的精确度的方法:看这个近似数的最后一位数字,它在哪个数位上就说明该近似数精确到哪一个数位.
2.取近似数的方法:求一个精确到某一数位的近似数时,对这一数位后面的那个数进行四舍五入.
活动2:按要求对下列各数取近似数,并和同伴交流结果.
(1)13.25(精确到个位);(2)1.794(精确到0.1);
(3)1.794(精确到0.01); (4)1 029500(精确到千位).
解:(1)13.25≈13;(2)1.794≈1.8;
(3)1.794≈1.79;(4)1029500=1.0295×106≈1.030×106.
1.小数点最后面的0不能随意添加或删除,否则就改变了近似数的精确度;
2.当数据较大时,其近似值可以用科学记数法表示.
这个0可以省略吗?
试一试:下列由四舍五入得到的近似数,各精确到哪一位?
(1)0.00407;(2)1.0;
(3)1.03万; (4)3.90×105.
解:(1)精确到0.00001(或十万分位);(2)精确到0.1(或十分位);
(3)1.03万=10 300,故精确到百位;
(4)3.90×105=390 000,故精确到千位.
1.若有汉字单位“万”之类的近似数,先把该数写成单位为“个”的数,再确定其精确度.
2.若用科学记数法表示的近似数,也需先将其写成原数,再确定其精确度.
活动小结
练一练
1.下列结论正确的是( )
A. 近似数4.230和4.23的精确度是一样的
B. 近似数89.0是精确到个位
C. 近似数0.00510与0.0510的精确度不一样
D. 近似数6万与近似数60 000的精确度相同
2.数4是4.3的近似值,其中4.3叫做真值,若一个数经四舍五入得到的近似数是12,则下列各数中不可能是12的真值的是( )
A. 12.38 B. 12.66 C. 11.99 D. 12.42
C
B
1.下列各题中的数,是准确数个数的有( )
(1)某校七年级男生有500名同学;
(2)从学校到火车站共有5个红绿灯路口;
(3)小明同学身高大约165cm;
(4)小红家与学校的距离是5千米.
A.1个 B.2个 C.3个 D.4个
B
2.下列各对近似数中,精确度一样的是( )
A.6.25与6.250 B.9.37与0.08
C.1.11与2.6 D.2.3×103与2300
3.用四舍五入法按要求对0.060 19分别取近似值,其中错误的是( )
A.0.1(精确到0.1) B.0.06(精确到百分位)
C.0.060(精确到百分位) D.0.060 2(精确到0.000 1)
B
C
4.用四舍五入法,按括号中的要求对下列各数取近似数.
(1)2.009(精确到0.01); (2)46 854 000(精确到万位);
(3)4.762×107(精确到百万位); (4)13亿(精确到十万位).
解:(1)2.009≈2.01;
(2)46 854 000≈4.685×107;
(3)4.762×107≈4.8×107;
(4)13亿≈1.300 0×109 .
针对本节课关键词“近似数”,说一说你都学到了哪些知识?
近似数
相关概念
应用
判别近似数、准确数
按要求取近似数
由近似数判断精确度
1.7 近似数
第1章 有理数
1.理解准确数、近似数的概念,并能辨别它们.
2.会用四舍五入法按要求取一个数的近似数,能说出一个近似数精确到的位数.
活动1:请同学们结合实际,回答下列问题.
(1)我们班有多少名同学,其中男生多少名,女生多少名?
(2)七年级上册数学课本有多少页?
(3)你的身高是多少?
(4)七年级上册数学课本有多宽?
任务一:能辨别准确数与近似数
与实际完全符合的数叫做准确数;
与实际数值很接近的数叫做近似数.
这些数据中,哪些数是与实际完全符合的?哪些数是与实际接近呢?
活动2:说出语句中的准确数和近似数,并和同伴交流数的辨别方法.
1.妈妈去买水果,买了8个苹果,大约3千克.
2.小民与小李买了2瓶水,4根黄瓜,6袋香巴拉牛肉干,约20元,然后骑车去3.5km外去郊游,大约玩了4.5小时回家.
3.我国共有56个民族.
4.举世瞩目的西气东输工程全长4000km.
近似数是由测量、称量、估计等等得到的数.近似数一般带有大约、左右、大概等等词语.
活动1:小明和小颖分别测量树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.读出下列测量结果.
任务二:能按要求取近似数及根据近似数确定精确度
小颖
小明
3cm
3.1cm
若需要的是3.06cm的树叶,谁的更符合要求?说说你的理由.
误差=近似值-准确值.
误差可能是正数,也可能是负数,误差的绝对值越小,近似值就越接近准确值.
近似数与准确数的接近程度,通常用精确度表示.
仿写:按四舍五入法对圆周率π取近似数时,有
π≈3 (精确到个位)
π≈3.1 (精确到0.1或叫做精确到十分位)
π≈3.14 (精确到0.01或叫做精确到百分位)
π≈3.142 (精确到 或叫做精确到 )
π≈3.141 6 (精确到 或叫做精确到 )
……
0.001
千分位
0.0001
万分位
1 0.1 十分位
4 0.01 百分位
2
6
小组讨论:观察上述近似数说说怎么确定一个近似数的精确度?那又是怎么取一个数的近似数?
活动小结
1.确定近似数的精确度的方法:看这个近似数的最后一位数字,它在哪个数位上就说明该近似数精确到哪一个数位.
2.取近似数的方法:求一个精确到某一数位的近似数时,对这一数位后面的那个数进行四舍五入.
活动2:按要求对下列各数取近似数,并和同伴交流结果.
(1)13.25(精确到个位);(2)1.794(精确到0.1);
(3)1.794(精确到0.01); (4)1 029500(精确到千位).
解:(1)13.25≈13;(2)1.794≈1.8;
(3)1.794≈1.79;(4)1029500=1.0295×106≈1.030×106.
1.小数点最后面的0不能随意添加或删除,否则就改变了近似数的精确度;
2.当数据较大时,其近似值可以用科学记数法表示.
这个0可以省略吗?
试一试:下列由四舍五入得到的近似数,各精确到哪一位?
(1)0.00407;(2)1.0;
(3)1.03万; (4)3.90×105.
解:(1)精确到0.00001(或十万分位);(2)精确到0.1(或十分位);
(3)1.03万=10 300,故精确到百位;
(4)3.90×105=390 000,故精确到千位.
1.若有汉字单位“万”之类的近似数,先把该数写成单位为“个”的数,再确定其精确度.
2.若用科学记数法表示的近似数,也需先将其写成原数,再确定其精确度.
活动小结
练一练
1.下列结论正确的是( )
A. 近似数4.230和4.23的精确度是一样的
B. 近似数89.0是精确到个位
C. 近似数0.00510与0.0510的精确度不一样
D. 近似数6万与近似数60 000的精确度相同
2.数4是4.3的近似值,其中4.3叫做真值,若一个数经四舍五入得到的近似数是12,则下列各数中不可能是12的真值的是( )
A. 12.38 B. 12.66 C. 11.99 D. 12.42
C
B
1.下列各题中的数,是准确数个数的有( )
(1)某校七年级男生有500名同学;
(2)从学校到火车站共有5个红绿灯路口;
(3)小明同学身高大约165cm;
(4)小红家与学校的距离是5千米.
A.1个 B.2个 C.3个 D.4个
B
2.下列各对近似数中,精确度一样的是( )
A.6.25与6.250 B.9.37与0.08
C.1.11与2.6 D.2.3×103与2300
3.用四舍五入法按要求对0.060 19分别取近似值,其中错误的是( )
A.0.1(精确到0.1) B.0.06(精确到百分位)
C.0.060(精确到百分位) D.0.060 2(精确到0.000 1)
B
C
4.用四舍五入法,按括号中的要求对下列各数取近似数.
(1)2.009(精确到0.01); (2)46 854 000(精确到万位);
(3)4.762×107(精确到百万位); (4)13亿(精确到十万位).
解:(1)2.009≈2.01;
(2)46 854 000≈4.685×107;
(3)4.762×107≈4.8×107;
(4)13亿≈1.300 0×109 .
针对本节课关键词“近似数”,说一说你都学到了哪些知识?
近似数
相关概念
应用
判别近似数、准确数
按要求取近似数
由近似数判断精确度
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
