2.2.3 整式加减 课件(共14张PPT) 沪科版七年级数学上册
文档属性
| 名称 | 2.2.3 整式加减 课件(共14张PPT) 沪科版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:22:45 | ||
图片预览






文档简介
(共14张PPT)
2.2 整式加减
3.整式加减
第2章 整式加减
1.能熟练进行整式的加减运算,结果按某个字母降幂(升幂)排列;
2.能将整式进行化简并求值.
活动1:将情境中得到的数与小组讨论,找出其中的规律.
情境:任意写一个两位数,交换它的十位数字与个位数字,又得到一个数,两个数相减.
任务一:能熟练进行整式加减运算
做一做:如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数如何表示?用整式加减运算验证发现的规律.
解:依题意有:原有的两位数为10a+b,则交换后的两位数为10b+a,
(10a+b)-(10b+a)=10a+b-10b-a=9a-9b=9(a-b),
故这些数的差是9的倍数.
活动2:同桌PK——看谁算的又快有准.
(1)-3(x+2y-1)- (4x-6y);(2)5a2b-[a3b+(3a2b-2a+4a3b)].
解:(1)原式=-3x-6y+3-2x+3y
=-5x-3y+3;
(2)原式=5a2b-(a3b+3a2b-2a+4a3b)
=5a2b-(5a3b+3a2b-2a)
=5a2b-5a3b-3a2b+2a
=-5a3b+2a2b+2a.
整式加减运算可归结为去括号、合并同类项.
观察这个答案排列有什么规律?
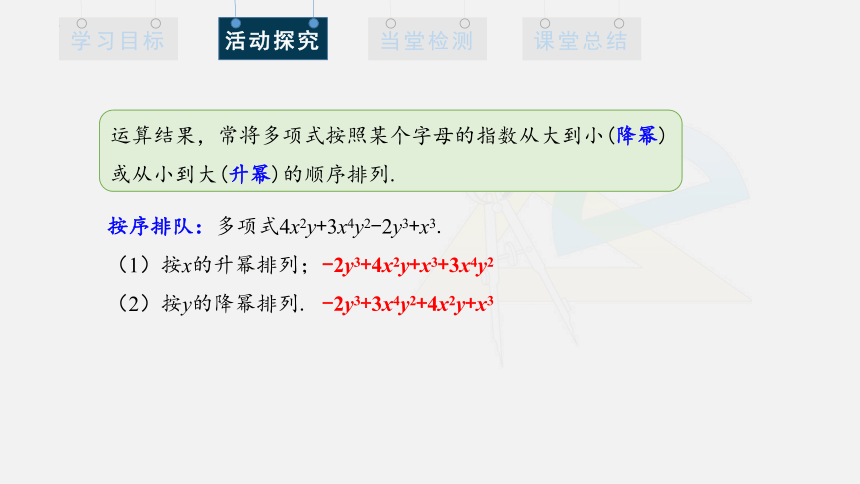
运算结果,常将多项式按照某个字母的指数从大到小(降幂)或从小到大(升幂)的顺序排列.
按序排队:多项式4x2y+3x4y2-2y3+x3.
(1)按x的升幂排列;
(2)按y的降幂排列.
-2y3+4x2y+x3+3x4y2
-2y3+3x4y2+4x2y+x3
活动3:已知A=3x2-2xy+y2,B=2x2+3xy-4y2.
求:(1)A-2B;(2)2A+B.
解:(1)A-2B=(3x2-2xy+y2)-2(2x2+3xy-4y2)
=3x2-2xy+y2-4x2-6xy+8y2
=-x2-8xy+9y2;
(2)2A+B=2(3x2-2xy+y2)+(2x2+3xy-4y2)
=6x2-4xy+2y2+2x2+3xy-4y2
=8x2-xy-2y2.
整体代入时需要加括号.
练一练
1.有一个多项式是下列四个单项式的和:-3a3b2、2、-2a2b、ab3,将这个多项式按字母b的降幂排列是( )
A.-3a3b2-2a2b+ab3+2 B.ab3-3a3b2-2a2b+2
C.2+ab3-3a3b2-2a2b D.-2a2b+ab3-3a3b2+2
2.已知A=a2+b2-c2,B=-4a2+2b2+3c2,若A+B+C=0,则多项式C为( )
A.5a2+3b2+2c2 B.5a2-3b2+4c2
C.3a2-3b2-2c2 D.3a2+3b2+4c2
B
C
将数值带入化简后的式子时,若数值是负数,要加上括号.
活动:看谁算的快.
求2(a2b-3ab)-3(ab+2ba2-1)的值,其中a=-2,b= .
任务二:会整式的化简求值
解:原式=2a2b-6ab-3ab-6a2b+3=-4a2b-9ab+3,
当a=-2,b= 时,原式= .
说一说做这类题的步骤.
整式的化简求值以整式加减运算为基础,具体步骤如下:
活动小结
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
变式:若代数式(2x2+ax-5y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-ab-b2)-(4a2+ab+b2)的值.
解:(2x2+ax-5y+b)-(2bx2-3x+5y-1)
=2x2+ax-5y+b-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x+(-5-5)y+b+1,
因为式子的值与字母x的取值无关,
所以2-2b=0,a+3=0,所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)
=3a2-3ab-3b2-4a2-ab-b2
=-a2-4ab-4b2
=-(-3)2-4×(-3)×1-4×12
=-1.
1.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7 B.-a2-a+1
C.a2+11a-7 D.a2-a+1
2.当a=-2时,3a2-2(2a2+a)+2(a2-3a)= .
A
20
3.计算:
(1)(9x-6y)-(5x-4y);(2)(x2-y2)-3(x2-2y2);
(3)(9a-2b)-[8a-(5b-2a)]+2c.
解:(1)(9x-6y)-(5x-4y)=4x-2y;
(2)(x2-y2)-3(x2-2y2)=-2x2+5y2;
(3)(9a-2b)-[8a-(5b-2a)]+2c=-a+3b+2c.
4.已知多项式2x2-x3+x与另一个多项式的和是x3+3x2-2x,求另一个多项式.
解:由题意得(x3+3x2-2x)-(2x2-x3+x)
=x3+3x2-2x-2x2+x3-x
=2x3+x2-3x,
所以另一个多项式为2x3+x2-3x.
回顾本节课,说一说你都学到了哪些知识?
整式加减
运算顺序
化简求值
降(升)幂排列
2.2 整式加减
3.整式加减
第2章 整式加减
1.能熟练进行整式的加减运算,结果按某个字母降幂(升幂)排列;
2.能将整式进行化简并求值.
活动1:将情境中得到的数与小组讨论,找出其中的规律.
情境:任意写一个两位数,交换它的十位数字与个位数字,又得到一个数,两个数相减.
任务一:能熟练进行整式加减运算
做一做:如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数如何表示?用整式加减运算验证发现的规律.
解:依题意有:原有的两位数为10a+b,则交换后的两位数为10b+a,
(10a+b)-(10b+a)=10a+b-10b-a=9a-9b=9(a-b),
故这些数的差是9的倍数.
活动2:同桌PK——看谁算的又快有准.
(1)-3(x+2y-1)- (4x-6y);(2)5a2b-[a3b+(3a2b-2a+4a3b)].
解:(1)原式=-3x-6y+3-2x+3y
=-5x-3y+3;
(2)原式=5a2b-(a3b+3a2b-2a+4a3b)
=5a2b-(5a3b+3a2b-2a)
=5a2b-5a3b-3a2b+2a
=-5a3b+2a2b+2a.
整式加减运算可归结为去括号、合并同类项.
观察这个答案排列有什么规律?
运算结果,常将多项式按照某个字母的指数从大到小(降幂)或从小到大(升幂)的顺序排列.
按序排队:多项式4x2y+3x4y2-2y3+x3.
(1)按x的升幂排列;
(2)按y的降幂排列.
-2y3+4x2y+x3+3x4y2
-2y3+3x4y2+4x2y+x3
活动3:已知A=3x2-2xy+y2,B=2x2+3xy-4y2.
求:(1)A-2B;(2)2A+B.
解:(1)A-2B=(3x2-2xy+y2)-2(2x2+3xy-4y2)
=3x2-2xy+y2-4x2-6xy+8y2
=-x2-8xy+9y2;
(2)2A+B=2(3x2-2xy+y2)+(2x2+3xy-4y2)
=6x2-4xy+2y2+2x2+3xy-4y2
=8x2-xy-2y2.
整体代入时需要加括号.
练一练
1.有一个多项式是下列四个单项式的和:-3a3b2、2、-2a2b、ab3,将这个多项式按字母b的降幂排列是( )
A.-3a3b2-2a2b+ab3+2 B.ab3-3a3b2-2a2b+2
C.2+ab3-3a3b2-2a2b D.-2a2b+ab3-3a3b2+2
2.已知A=a2+b2-c2,B=-4a2+2b2+3c2,若A+B+C=0,则多项式C为( )
A.5a2+3b2+2c2 B.5a2-3b2+4c2
C.3a2-3b2-2c2 D.3a2+3b2+4c2
B
C
将数值带入化简后的式子时,若数值是负数,要加上括号.
活动:看谁算的快.
求2(a2b-3ab)-3(ab+2ba2-1)的值,其中a=-2,b= .
任务二:会整式的化简求值
解:原式=2a2b-6ab-3ab-6a2b+3=-4a2b-9ab+3,
当a=-2,b= 时,原式= .
说一说做这类题的步骤.
整式的化简求值以整式加减运算为基础,具体步骤如下:
活动小结
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
变式:若代数式(2x2+ax-5y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求代数式3(a2-ab-b2)-(4a2+ab+b2)的值.
解:(2x2+ax-5y+b)-(2bx2-3x+5y-1)
=2x2+ax-5y+b-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x+(-5-5)y+b+1,
因为式子的值与字母x的取值无关,
所以2-2b=0,a+3=0,所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)
=3a2-3ab-3b2-4a2-ab-b2
=-a2-4ab-4b2
=-(-3)2-4×(-3)×1-4×12
=-1.
1.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7 B.-a2-a+1
C.a2+11a-7 D.a2-a+1
2.当a=-2时,3a2-2(2a2+a)+2(a2-3a)= .
A
20
3.计算:
(1)(9x-6y)-(5x-4y);(2)(x2-y2)-3(x2-2y2);
(3)(9a-2b)-[8a-(5b-2a)]+2c.
解:(1)(9x-6y)-(5x-4y)=4x-2y;
(2)(x2-y2)-3(x2-2y2)=-2x2+5y2;
(3)(9a-2b)-[8a-(5b-2a)]+2c=-a+3b+2c.
4.已知多项式2x2-x3+x与另一个多项式的和是x3+3x2-2x,求另一个多项式.
解:由题意得(x3+3x2-2x)-(2x2-x3+x)
=x3+3x2-2x-2x2+x3-x
=2x3+x2-3x,
所以另一个多项式为2x3+x2-3x.
回顾本节课,说一说你都学到了哪些知识?
整式加减
运算顺序
化简求值
降(升)幂排列
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
