2023-2024学年浙教版数学九年级上册期末综合练习(一)(无答案)
文档属性
| 名称 | 2023-2024学年浙教版数学九年级上册期末综合练习(一)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 477.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览


文档简介
2023-2024学年浙教版数学九年级上册期末综合练习(一)
一、选择题
1.二次数y=x2+6x+1图象的对称轴是( )
A.x=6 B.x=﹣6 C.x=﹣3 D.x=4
2.一个口袋中有4个白球,1个红球,7个黄球,搅匀后随机从袋中摸出1个球,则摸出的球是黄球的概率是( )
A. B. C. D.
3.如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是( )
A.①④ B.①③
C.②③ D.②④
4.某班学生做“用频率估计概率”的实验时,得到的实验结果成如图所示的统计图,则符合这一结果的实验可能是( )
A.掷一个质地均匀的正六面体骰子,向上的面点数是4
B.扔一枚面额一元的硬币,正面朝上
C.在“石头、剪刀、布”的游戏中,某人随机出的是“剪刀”
D.从标有1,2,3,4,5,6的六张卡片中任抽一张,抽到的卡片上标有奇数
5.如图,ABCD是的内接四边形,,则的度数是( )
A.50° B.100° C.130° D.120°
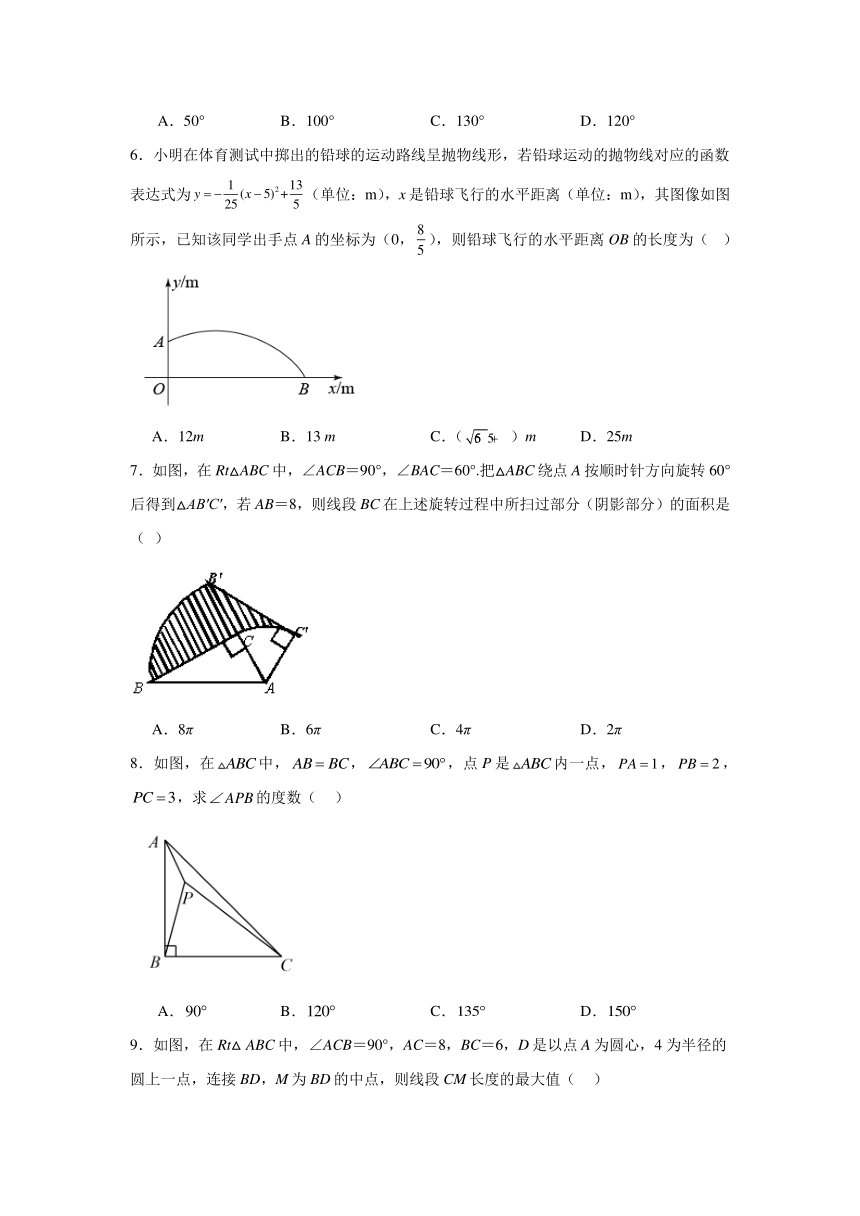
6.小明在体育测试中掷出的铅球的运动路线呈抛物线形,若铅球运动的抛物线对应的函数表达式为(单位:m),x是铅球飞行的水平距离(单位:m),其图像如图所示,已知该同学出手点A的坐标为(0,),则铅球飞行的水平距离OB的长度为( )
A.12m B.13 m C.()m D.25m
7.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=8,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
A.8π B.6π C.4π D.2π
8.如图,在中,,,点P是内一点,,,,求的度数( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是以点A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最大值( )
A.14 B.7 C.9 D.6
10.如图,是二次函数的图象的一部分,给出下列命题:①;②;③的两根分别为、(),则,;④.其中正确的命题是( )
A.①③ B.②③ C.①② D.①②③④
二、填空题
11.一个不透明的盒子中装有若干个红球和个黑球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黑球的频率稳定在左右,则盒子中红球的个数约为 .
12.如图,,直线,与这三条平行线分别交于点A,C,E,和点B,D,F.已知,则的长为 .
13.已知二次函数的图象上有两点,,则,的大小关系为 .
14.若的半径为2,则的圆心角所对的弧长是 .
15.如图,半圆O的直径,弦,平分,则的长为 .
16.已知抛物线y=x2-mx+m-2.(其中m是常数),不论m取何值,抛物线都经过一个定点,则这个定点的坐标为 .
17.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 .
三、解答题
18.如图,两个转盘中指针落在每个数字上的机会相等,现同时转动、两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗 如果不公平,对谁更有利?请你利用树状图或列表法说明理由.
19.已知二次函数的部分图象如图所示.
(1)求这个二次函数的解析式:
(2)直接写出满足时,x的取值范围.
20.如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
(1)△ABC与△A1B1C1关于某条直线m对称,画出对称轴m.
(2)画出△A1B1C1绕原点O顺时针旋转90°所得的△A2B2C2.此时点A2的坐标为________;
求出点A1旋转到点A2的路径长.(结果保留根号)
21.如图,在△ABC中,点D是AB上一点(不与A、B重合),过点D作DEBC,交AC于点E.连接CD,若∠ACD=∠B.
(1)求证:CD2=DE BC;
(2)若DE=3,BC=4,求的值.
22.P为等边内的一点,,将绕点B顺时针旋转到位置.
(1)判断的形状,并说明理由;
(2)求的度数.
23.如图,在四边形 中,,,, 为 的外接圆.
(1) 如图 ,求证: 是 的切线.
(2) 如图 , 交 于点 ,过点 作 ,垂足为 ,交 于点 .
①求证:.
②若 ,,求 的长.
24.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
销售单价(元) 40+x
销售量y(件)
销售玩具获得利润W(元)
(2)在(1)问的条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?
(3)在(1)问的条件下,若商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
25.如图所示,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,连接AC,已知B(﹣1,0),点A(3,0).
(1)求抛物线的解析式;
(2)若点P是抛物线上位于直线AC下方的一点,且BE∥AC交抛物线于点E,连接PB交AC于点F,连接EF、PE,求△PEF面积的最大值并求出此时点P的坐标;
(3)在(2)的条件下,将抛物线向右平移至经过点P,得到抛物线y',若N为抛物线y'对称轴上的一点,且以A、P、N为顶点的三角形是直角三角形,请直接写出点N的坐标.
一、选择题
1.二次数y=x2+6x+1图象的对称轴是( )
A.x=6 B.x=﹣6 C.x=﹣3 D.x=4
2.一个口袋中有4个白球,1个红球,7个黄球,搅匀后随机从袋中摸出1个球,则摸出的球是黄球的概率是( )
A. B. C. D.
3.如图,四个三角形的顶点都在方格子的格点上,下列两个三角形中相似的是( )
A.①④ B.①③
C.②③ D.②④
4.某班学生做“用频率估计概率”的实验时,得到的实验结果成如图所示的统计图,则符合这一结果的实验可能是( )
A.掷一个质地均匀的正六面体骰子,向上的面点数是4
B.扔一枚面额一元的硬币,正面朝上
C.在“石头、剪刀、布”的游戏中,某人随机出的是“剪刀”
D.从标有1,2,3,4,5,6的六张卡片中任抽一张,抽到的卡片上标有奇数
5.如图,ABCD是的内接四边形,,则的度数是( )
A.50° B.100° C.130° D.120°
6.小明在体育测试中掷出的铅球的运动路线呈抛物线形,若铅球运动的抛物线对应的函数表达式为(单位:m),x是铅球飞行的水平距离(单位:m),其图像如图所示,已知该同学出手点A的坐标为(0,),则铅球飞行的水平距离OB的长度为( )
A.12m B.13 m C.()m D.25m
7.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=8,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
A.8π B.6π C.4π D.2π
8.如图,在中,,,点P是内一点,,,,求的度数( )
A. B. C. D.
9.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D是以点A为圆心,4为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最大值( )
A.14 B.7 C.9 D.6
10.如图,是二次函数的图象的一部分,给出下列命题:①;②;③的两根分别为、(),则,;④.其中正确的命题是( )
A.①③ B.②③ C.①② D.①②③④
二、填空题
11.一个不透明的盒子中装有若干个红球和个黑球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黑球的频率稳定在左右,则盒子中红球的个数约为 .
12.如图,,直线,与这三条平行线分别交于点A,C,E,和点B,D,F.已知,则的长为 .
13.已知二次函数的图象上有两点,,则,的大小关系为 .
14.若的半径为2,则的圆心角所对的弧长是 .
15.如图,半圆O的直径,弦,平分,则的长为 .
16.已知抛物线y=x2-mx+m-2.(其中m是常数),不论m取何值,抛物线都经过一个定点,则这个定点的坐标为 .
17.如图,在平面直角坐标系中,点A的坐标为,点B的坐标为,点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 .
三、解答题
18.如图,两个转盘中指针落在每个数字上的机会相等,现同时转动、两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗 如果不公平,对谁更有利?请你利用树状图或列表法说明理由.
19.已知二次函数的部分图象如图所示.
(1)求这个二次函数的解析式:
(2)直接写出满足时,x的取值范围.
20.如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
(1)△ABC与△A1B1C1关于某条直线m对称,画出对称轴m.
(2)画出△A1B1C1绕原点O顺时针旋转90°所得的△A2B2C2.此时点A2的坐标为________;
求出点A1旋转到点A2的路径长.(结果保留根号)
21.如图,在△ABC中,点D是AB上一点(不与A、B重合),过点D作DEBC,交AC于点E.连接CD,若∠ACD=∠B.
(1)求证:CD2=DE BC;
(2)若DE=3,BC=4,求的值.
22.P为等边内的一点,,将绕点B顺时针旋转到位置.
(1)判断的形状,并说明理由;
(2)求的度数.
23.如图,在四边形 中,,,, 为 的外接圆.
(1) 如图 ,求证: 是 的切线.
(2) 如图 , 交 于点 ,过点 作 ,垂足为 ,交 于点 .
①求证:.
②若 ,,求 的长.
24.某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
销售单价(元) 40+x
销售量y(件)
销售玩具获得利润W(元)
(2)在(1)问的条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?
(3)在(1)问的条件下,若商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
25.如图所示,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,连接AC,已知B(﹣1,0),点A(3,0).
(1)求抛物线的解析式;
(2)若点P是抛物线上位于直线AC下方的一点,且BE∥AC交抛物线于点E,连接PB交AC于点F,连接EF、PE,求△PEF面积的最大值并求出此时点P的坐标;
(3)在(2)的条件下,将抛物线向右平移至经过点P,得到抛物线y',若N为抛物线y'对称轴上的一点,且以A、P、N为顶点的三角形是直角三角形,请直接写出点N的坐标.
同课章节目录
