第1章 三角形 单元测试卷(无答案) 2023-—2024学年鲁教版(五四制)七年级数学上册
文档属性
| 名称 | 第1章 三角形 单元测试卷(无答案) 2023-—2024学年鲁教版(五四制)七年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览



文档简介
《第1章 三角形》单元测试卷2023-2024学年鲁教五四新版七年级上册数学
一.选择题
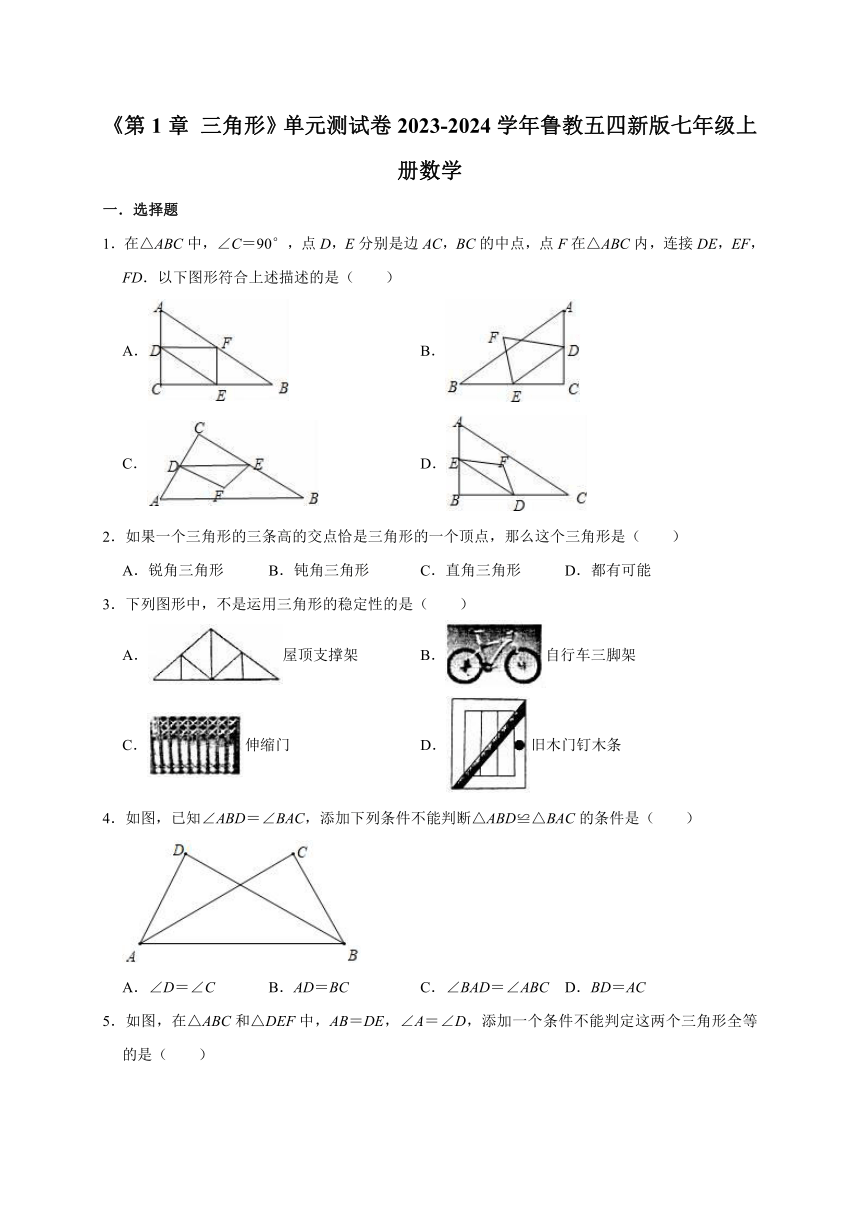
1.在△ABC中,∠C=90°,点D,E分别是边AC,BC的中点,点F在△ABC内,连接DE,EF,FD.以下图形符合上述描述的是( )
A. B.
C. D.
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.都有可能
3.下列图形中,不是运用三角形的稳定性的是( )
A.屋顶支撑架 B.自行车三脚架
C.伸缩门 D.旧木门钉木条
4.如图,已知∠ABD=∠BAC,添加下列条件不能判断△ABD≌△BAC的条件是( )
A.∠D=∠C B.AD=BC C.∠BAD=∠ABC D.BD=AC
5.如图,在△ABC和△DEF中,AB=DE,∠A=∠D,添加一个条件不能判定这两个三角形全等的是( )
A.AC=DF B.∠B=∠E C.BC=EF D.∠C=∠F
6.如图,已知∠ABC=∠DCB,AC与DB相交于点O.若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( )
A.∠A=∠D B.AB=CD C.∠ACB=∠DBC D.AC=BD
7.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
8.一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
9如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为
A. B. C. D.
10.已知 , 为 的平分线,,,, 为 的平分线上的若干点如图①,连接 ,,则有 对全等三角形;如图②,连接 ,,,,则有 对全等三角形;如图③,连接 ,,,,,,则有 对全等三角形;依此规律,第⑧个图形中有全等三角形
A. 对 B. 对 C. 对 D. 对
二填空题
11.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
12.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形.
13.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a= ,b= ,c= .
14.如图,在△ABC中,D是AB中点,E是BC边上一点,且BE=4EC,CD与AE交于点F,连接BF.若△BEF的面积是4,则△ABC的面积是 .
15.如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
三.解答题
16.已知线段AB=8cm,BC=3cm.
(1)线段AC的长度能否确定? (填“能”或“不能”即可);
(2)是否存在使A、C之间的距离最短的情形?若存在,求出此时AC的长度;若不存在,说明理由.
(3)能比较BA+BC与AC的大小吗?为什么?
17.如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
18.如图, MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N 、Q,且MS=PS.
求证:MN=QS.
19.如图①,△ABC中,∠ABC,∠ACB的平分线交于O点,过O点作BC平行线交AB,AC于E,F.
(1)试说明:EO=BE;
(2)探究图①中线段EF与BE,CF间的关系,并说明理由;
(3)探究图②,△ABC中若∠ABC的平分线与△ABC的外角平分线交于O,过点O作BC的平行线交AB于E,交AC于F,这时EF与BE,CF的关系又如何?请直接写出关系,不需要说明理由.
20.【概念认识】
如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC= °;
(2)如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;
【延伸推广】
(3)在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=n°,直接写出∠BPC的度数.(用含m、n的代数式表示)
一.选择题
1.在△ABC中,∠C=90°,点D,E分别是边AC,BC的中点,点F在△ABC内,连接DE,EF,FD.以下图形符合上述描述的是( )
A. B.
C. D.
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.都有可能
3.下列图形中,不是运用三角形的稳定性的是( )
A.屋顶支撑架 B.自行车三脚架
C.伸缩门 D.旧木门钉木条
4.如图,已知∠ABD=∠BAC,添加下列条件不能判断△ABD≌△BAC的条件是( )
A.∠D=∠C B.AD=BC C.∠BAD=∠ABC D.BD=AC
5.如图,在△ABC和△DEF中,AB=DE,∠A=∠D,添加一个条件不能判定这两个三角形全等的是( )
A.AC=DF B.∠B=∠E C.BC=EF D.∠C=∠F
6.如图,已知∠ABC=∠DCB,AC与DB相交于点O.若添加一个条件,仍不能判定△ABC≌△DCB,则这个条件是( )
A.∠A=∠D B.AB=CD C.∠ACB=∠DBC D.AC=BD
7.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
8.一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
A.80° B.95° C.100° D.110°
9如图,将一张含有 角的三角形纸片的两个顶点叠放在矩形的两条对边上,若 ,则 的大小为
A. B. C. D.
10.已知 , 为 的平分线,,,, 为 的平分线上的若干点如图①,连接 ,,则有 对全等三角形;如图②,连接 ,,,,则有 对全等三角形;如图③,连接 ,,,,,,则有 对全等三角形;依此规律,第⑧个图形中有全等三角形
A. 对 B. 对 C. 对 D. 对
二填空题
11.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
12.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是 三角形.
13.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a= ,b= ,c= .
14.如图,在△ABC中,D是AB中点,E是BC边上一点,且BE=4EC,CD与AE交于点F,连接BF.若△BEF的面积是4,则△ABC的面积是 .
15.如图,在△ABC中,∠A=x°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…,∠An﹣1BC和∠An﹣1CD的平分线交于点An,则∠An= .
三.解答题
16.已知线段AB=8cm,BC=3cm.
(1)线段AC的长度能否确定? (填“能”或“不能”即可);
(2)是否存在使A、C之间的距离最短的情形?若存在,求出此时AC的长度;若不存在,说明理由.
(3)能比较BA+BC与AC的大小吗?为什么?
17.如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
18.如图, MS⊥PS,MN⊥SN,PQ⊥SN,垂足分别为S、N 、Q,且MS=PS.
求证:MN=QS.
19.如图①,△ABC中,∠ABC,∠ACB的平分线交于O点,过O点作BC平行线交AB,AC于E,F.
(1)试说明:EO=BE;
(2)探究图①中线段EF与BE,CF间的关系,并说明理由;
(3)探究图②,△ABC中若∠ABC的平分线与△ABC的外角平分线交于O,过点O作BC的平行线交AB于E,交AC于F,这时EF与BE,CF的关系又如何?请直接写出关系,不需要说明理由.
20.【概念认识】
如图①,在∠ABC中,若∠ABD=∠DBE=∠EBC,则BD,BE叫做∠ABC的“三分线”.其中,BD是“邻AB三分线”,BE是“邻BC三分线”.
【问题解决】
(1)如图②,在△ABC中,∠A=70°,∠B=45°,若∠B的三分线BD交AC于点D,则∠BDC= °;
(2)如图③,在△ABC中,BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线,且BP⊥CP,求∠A的度数;
【延伸推广】
(3)在△ABC中,∠ACD是△ABC的外角,∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A=m°,∠B=n°,直接写出∠BPC的度数.(用含m、n的代数式表示)
