14.1 全等三角形课件(共16张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 14.1 全等三角形课件(共16张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
第十四章 全等三角形
14.1 全等三角形
1.理解全等三角形的概念,能识别全等三角形中对应边、对应角.
2.掌握全等三角形对应边相等、对应角相等的性质.
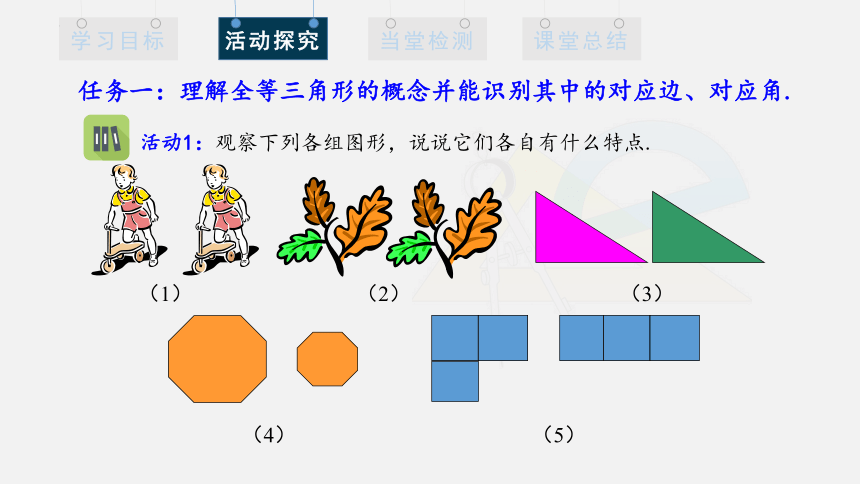
任务一:理解全等三角形的概念并能识别其中的对应边、对应角.
活动1:观察下列各组图形,说说它们各自有什么特点.
(1)
(2)
(3)
(4)
(5)
活动小结
全等形定义:能够完全重合的两个图形叫做全等形.
如果两个图形全等,它们的形状和大小一定都相等.
全等三角形定义:能够完全重合的两个三角形叫做全等三角形.
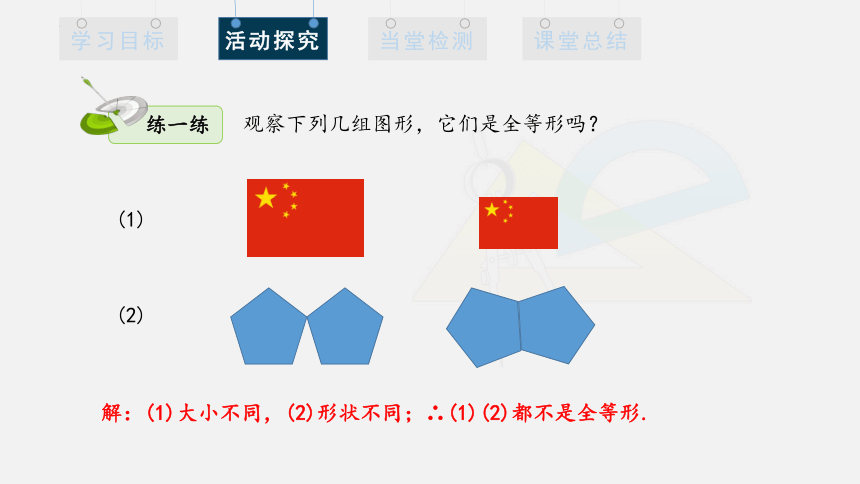
观察下列几组图形,它们是全等形吗?
(1)
(2)
解:(1)大小不同,(2)形状不同;∴(1)(2)都不是全等形.
练一练
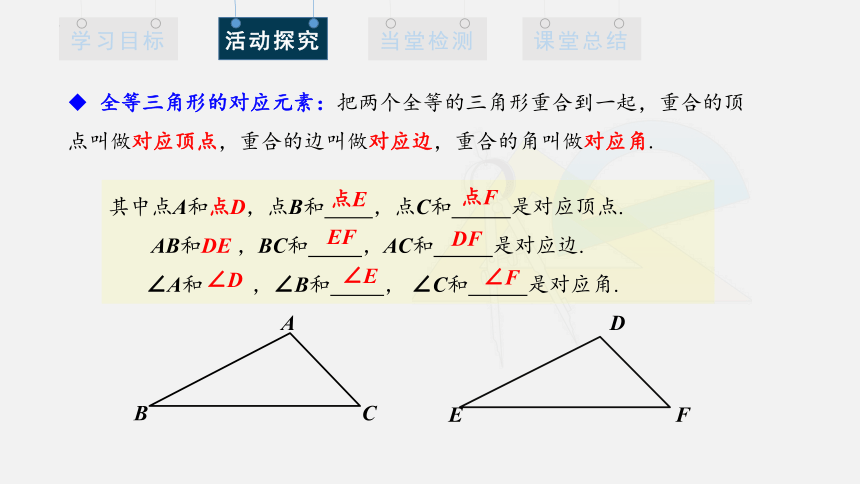
其中点A和点D,点B和 ,点C和 是对应顶点.
AB和DE ,BC和 ,AC和 是对应边.
∠A和 ,∠B和 , ∠C和 是对应角.
B
C
A
E
F
D
点E
点F
EF
DF
∠D
∠E
∠F
全等三角形的对应元素:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
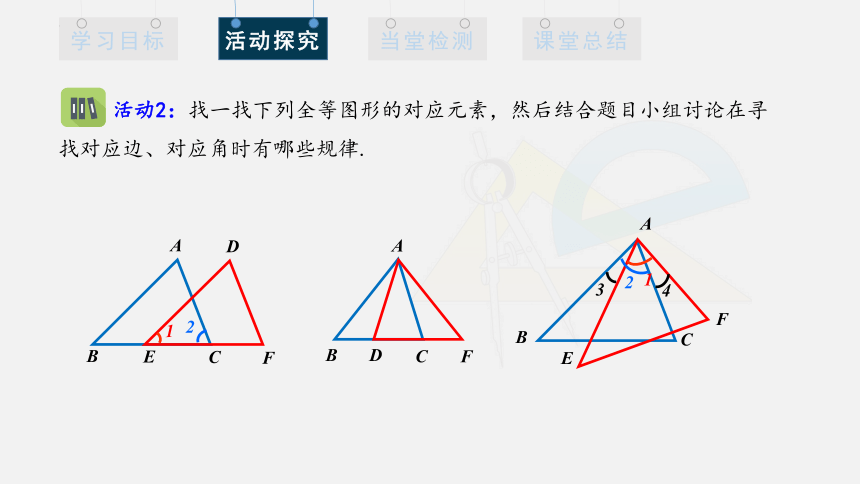
活动2:找一找下列全等图形的对应元素,然后结合题目小组讨论在寻找对应边、对应角时有哪些规律.
A
D
F
C
E
B
1
2
E
A
B
C
F
1
2
3
4
A
B
C
D
F
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边,最小的边也是对应边;
5. 两个全等三角形最大的角是对应角,最小的角也是对应角.
活动小结
任务二:掌握全等三角形对应边相等、对应角相等的性质.
活动1:和同伴一起交流,说说全等三角形的对应边、对应角分别有什么数量关系?
A
B
C
A'
B'
C'
全等三角形的对应边相等,对应角相等.
思考:如何用几何语言表示全等三角形的性质?
△ A B C ≌ △ F D E
A
B
C
E
D
F
注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
全等的表示:“全等”用符号“≌”表示,读作“全等于”.
A
B
C
D
E
F
全等三角形的性质:全等三角形的对应边相等,对应角相等.
几何语言:如图:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
活动小结
A
B
C
D
E
F
解:∵ △ABC≌△DEF 且 EF=7,∠B = 50°;
∴ BC = EF = 7,∠B = ∠E = 50°;
(全等三角形,对应的边、角相等)
∴ ∠EFD=60°;
∵ BC = BF + CF 且 BF = 4;
∴ CF = 3.
活动2:如图,△ABC≌△DEF,∠A=∠D=70°、 ∠B=50°,BF=4,EF=7,求:∠EFD的度数和CF的长.
1.下列说法:①用同一张底片冲洗出来的10张1寸相片是全等形;
②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;
④全等形的面积一定相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
∠D
∠BAD
∠ABD
AD
BD
BA
B
C
D
A
角
角
角
边
边
边
AB=
AC=
BC=
∠BAC=
∠ABC=
∠C=
2.如图,已知△ABC≌△BAD,请指出图中的对应边和对应角.
3. 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.
解:(1)AB与DC,AC与DB,BC与CB是对应边;
∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角;
(2)∵ △ABC≌△DCB,且AB=3,DB=4,∠A=60°;
∴ AC = DB = 4,DC = AB = 3,∠D =∠A = 60°.
D
A
C
B
O
性质:对应边相等,对应角相等.
全等三角形
概念:能够完全重合的两个三角形.
说一说你本堂课都学到了哪些知识?
第十四章 全等三角形
14.1 全等三角形
1.理解全等三角形的概念,能识别全等三角形中对应边、对应角.
2.掌握全等三角形对应边相等、对应角相等的性质.
任务一:理解全等三角形的概念并能识别其中的对应边、对应角.
活动1:观察下列各组图形,说说它们各自有什么特点.
(1)
(2)
(3)
(4)
(5)
活动小结
全等形定义:能够完全重合的两个图形叫做全等形.
如果两个图形全等,它们的形状和大小一定都相等.
全等三角形定义:能够完全重合的两个三角形叫做全等三角形.
观察下列几组图形,它们是全等形吗?
(1)
(2)
解:(1)大小不同,(2)形状不同;∴(1)(2)都不是全等形.
练一练
其中点A和点D,点B和 ,点C和 是对应顶点.
AB和DE ,BC和 ,AC和 是对应边.
∠A和 ,∠B和 , ∠C和 是对应角.
B
C
A
E
F
D
点E
点F
EF
DF
∠D
∠E
∠F
全等三角形的对应元素:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
活动2:找一找下列全等图形的对应元素,然后结合题目小组讨论在寻找对应边、对应角时有哪些规律.
A
D
F
C
E
B
1
2
E
A
B
C
F
1
2
3
4
A
B
C
D
F
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边,最小的边也是对应边;
5. 两个全等三角形最大的角是对应角,最小的角也是对应角.
活动小结
任务二:掌握全等三角形对应边相等、对应角相等的性质.
活动1:和同伴一起交流,说说全等三角形的对应边、对应角分别有什么数量关系?
A
B
C
A'
B'
C'
全等三角形的对应边相等,对应角相等.
思考:如何用几何语言表示全等三角形的性质?
△ A B C ≌ △ F D E
A
B
C
E
D
F
注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
全等的表示:“全等”用符号“≌”表示,读作“全等于”.
A
B
C
D
E
F
全等三角形的性质:全等三角形的对应边相等,对应角相等.
几何语言:如图:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
活动小结
A
B
C
D
E
F
解:∵ △ABC≌△DEF 且 EF=7,∠B = 50°;
∴ BC = EF = 7,∠B = ∠E = 50°;
(全等三角形,对应的边、角相等)
∴ ∠EFD=60°;
∵ BC = BF + CF 且 BF = 4;
∴ CF = 3.
活动2:如图,△ABC≌△DEF,∠A=∠D=70°、 ∠B=50°,BF=4,EF=7,求:∠EFD的度数和CF的长.
1.下列说法:①用同一张底片冲洗出来的10张1寸相片是全等形;
②我国国旗上的4颗小五角星是全等形;③所有的正方形是全等形;
④全等形的面积一定相等.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
C
∠D
∠BAD
∠ABD
AD
BD
BA
B
C
D
A
角
角
角
边
边
边
AB=
AC=
BC=
∠BAC=
∠ABC=
∠C=
2.如图,已知△ABC≌△BAD,请指出图中的对应边和对应角.
3. 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.
解:(1)AB与DC,AC与DB,BC与CB是对应边;
∠A与∠D,∠ABC与∠DCB,∠ACB与∠DBC是对应角;
(2)∵ △ABC≌△DCB,且AB=3,DB=4,∠A=60°;
∴ AC = DB = 4,DC = AB = 3,∠D =∠A = 60°.
D
A
C
B
O
性质:对应边相等,对应角相等.
全等三角形
概念:能够完全重合的两个三角形.
说一说你本堂课都学到了哪些知识?
