13.2 命题与证明 第4课时 课件(共15张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 13.2 命题与证明 第4课时 课件(共15张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:44:48 | ||
图片预览




文档简介
(共15张PPT)
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.4 三角形内角和
定理的证明及推论
1.掌握“三角形内角和定理”的证明及其简单应用.
2.掌握三角形内角和定理的推论1和推论2.
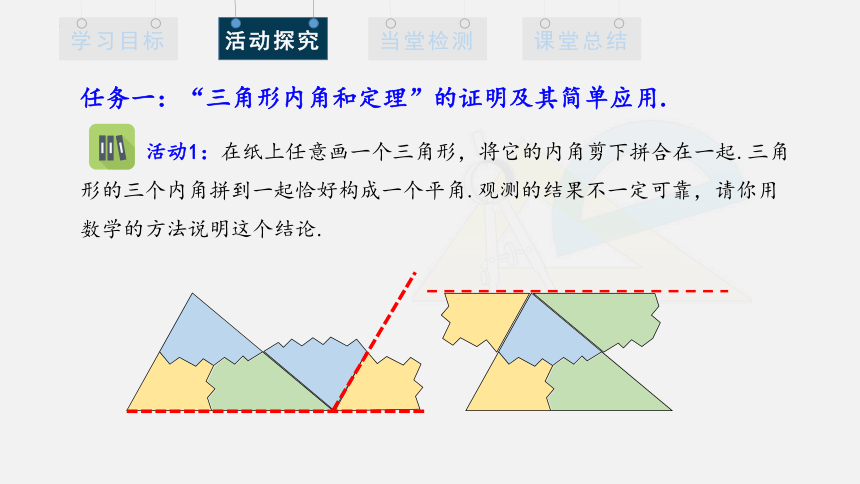
任务一:“三角形内角和定理”的证明及其简单应用.
活动1:在纸上任意画一个三角形,将它的内角剪下拼合在一起.三角形的三个内角拼到一起恰好构成一个平角.观测的结果不一定可靠,请你用数学的方法说明这个结论.
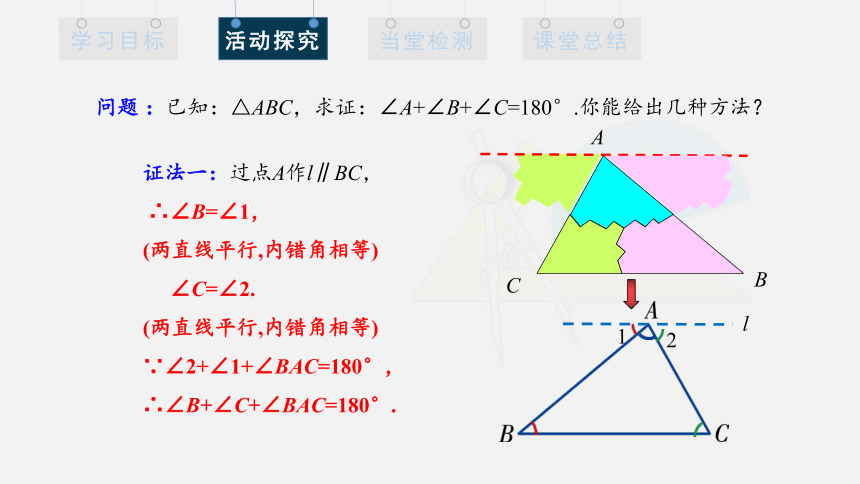
问题 :已知:△ABC,求证:∠A+∠B+∠C=180°.你能给出几种方法?
证法一:过点A作l∥BC,
∴∠B=∠1,
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
A
C
B
l
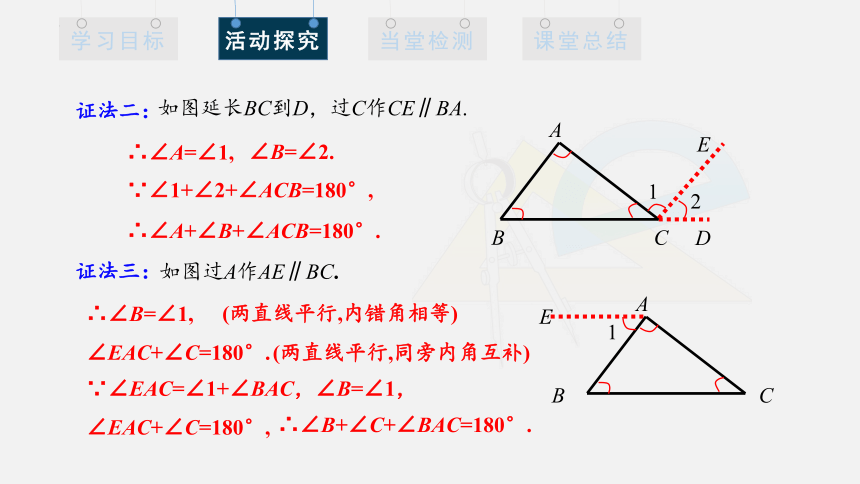
证法二:
如图延长BC到D,过C作CE∥BA.
∴∠A=∠1,
∠B=∠2.
∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
E
2
1
D
A
B
C
证法三:
如图过A作AE∥BC.
∴∠B=∠1,
(两直线平行,内错角相等)
∠EAC+∠C=180°.
(两直线平行,同旁内角互补)
∵∠EAC=∠1+∠BAC,∠B=∠1,∠EAC+∠C=180°,
∴∠B+∠C+∠BAC=180°.
1
E
A
B
C
思考:多种方法证明三角形内角和等于180°的核心是什么?
A
B
C
D
E
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
借助平行线的“移角”的功能,将三个角转化成一个平角.
为了证明的需要,我们在原来的图形上添画的线叫做辅助线.
(在平面几何里,辅助线通常画成虚线).
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
活动小结
活动2:利用刚刚所学知识,回答下列问题.
在△ABC中,∠B = ∠ACB = 70°且CD是∠ACB的角平分线,求∠1的度数.
解:∵ ∠B = ∠ACB = 70°;(已知)
∴ ∠A = 40°;(三角形的内角和定理)
∵ CD是∠ ACB的角平分线;
∴ ∠ACD = 35°;(角平分线定义)
∴ ∠1 = 105° (三角形的内角和定理).
A
B
C
D
1
任务二:掌握三角形内角和定理的推论1和推论2.
活动1:和同伴一起交流,完成下列问题.
问题1:在△ABC中,∠C=90 °,求:∠A+∠B的度数?由此你能得到什么结论?
问题2:在△ABC中,∠A+∠B=90 °,则∠C度数为多少?由此你能得到什么结论?
分析:根据三角形内角和定理解答即可;
解:在△ABC中,∵ ∠ A + ∠ B + ∠ C = 180°;
又∵ ∠C= 90°,即:△ABC是直角三角形;
∴ ∠A + ∠ B = 90°;
结论:直角三角形的两锐角互余.
问题1:在△ABC中,∠C=90°,求: ∠A+∠B的度数?由此你能得到什么结论?
问题2:在△ABC中,∠A+∠B=90°,则∠C度数为多少?由此你能得到什么结论?
解:在△ABC中,∵ ∠A + ∠B + ∠C = 180°;
又∵ ∠A + ∠B = 90°;
∴ ∠ C = 90°,即:△ABC是直角三角形;
结论:有两个角互余的三角形是直角三角形.
三角形内角和推论1:直角三角形的两锐角互余;
三角形内角和推论2:有两个角互余的三角形是直角三角形.
推论:像这样,由基本事实、定理直接得出的真命题叫做推论.
活动小结
1.在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A. 50° B. 45°
C. 40° D. 30°
A
2.在直角三角形中,有一个锐角是另一个锐角的2倍,则这两个锐角的度数是 和 .
30°
60°
3.已知:如图所示,△ABC中,∠AFB=135°,∠A、∠B的平分线AD、 BE交于F,试证明△ABC为直角三角形.
A
B
C
F
E
D
证明:∵在△AFB中,∠AFB=135°,(已知)
∴∠FAB+∠FBA=180°-135°=45°(三角形内角和定理)
∵AD、BE平分∠CAB、∠CBA,(已知)
∴∠CAB=2∠FAB,∠CBA=2∠FBA(角平分线的性质)
∴∠CAB+∠CBA=2(∠FAB+∠FBA)=90°,(等量代换)
∴△ABC为直角三角形.(有两个角互余的三角形是直角三角形)
证法
推论
转化为一个平角
或同旁内角互补
三角形的内角和等于180 °
作辅助线
转化思想
1.直角三角形的两个锐角互余.
2.有两个角互余的三角形是直角三角形.
针对本课关键词“三角形内角和定理的证明及推论”,说说你学到了什么.
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.4 三角形内角和
定理的证明及推论
1.掌握“三角形内角和定理”的证明及其简单应用.
2.掌握三角形内角和定理的推论1和推论2.
任务一:“三角形内角和定理”的证明及其简单应用.
活动1:在纸上任意画一个三角形,将它的内角剪下拼合在一起.三角形的三个内角拼到一起恰好构成一个平角.观测的结果不一定可靠,请你用数学的方法说明这个结论.
问题 :已知:△ABC,求证:∠A+∠B+∠C=180°.你能给出几种方法?
证法一:过点A作l∥BC,
∴∠B=∠1,
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
A
C
B
l
证法二:
如图延长BC到D,过C作CE∥BA.
∴∠A=∠1,
∠B=∠2.
∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
E
2
1
D
A
B
C
证法三:
如图过A作AE∥BC.
∴∠B=∠1,
(两直线平行,内错角相等)
∠EAC+∠C=180°.
(两直线平行,同旁内角互补)
∵∠EAC=∠1+∠BAC,∠B=∠1,∠EAC+∠C=180°,
∴∠B+∠C+∠BAC=180°.
1
E
A
B
C
思考:多种方法证明三角形内角和等于180°的核心是什么?
A
B
C
D
E
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
借助平行线的“移角”的功能,将三个角转化成一个平角.
为了证明的需要,我们在原来的图形上添画的线叫做辅助线.
(在平面几何里,辅助线通常画成虚线).
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
活动小结
活动2:利用刚刚所学知识,回答下列问题.
在△ABC中,∠B = ∠ACB = 70°且CD是∠ACB的角平分线,求∠1的度数.
解:∵ ∠B = ∠ACB = 70°;(已知)
∴ ∠A = 40°;(三角形的内角和定理)
∵ CD是∠ ACB的角平分线;
∴ ∠ACD = 35°;(角平分线定义)
∴ ∠1 = 105° (三角形的内角和定理).
A
B
C
D
1
任务二:掌握三角形内角和定理的推论1和推论2.
活动1:和同伴一起交流,完成下列问题.
问题1:在△ABC中,∠C=90 °,求:∠A+∠B的度数?由此你能得到什么结论?
问题2:在△ABC中,∠A+∠B=90 °,则∠C度数为多少?由此你能得到什么结论?
分析:根据三角形内角和定理解答即可;
解:在△ABC中,∵ ∠ A + ∠ B + ∠ C = 180°;
又∵ ∠C= 90°,即:△ABC是直角三角形;
∴ ∠A + ∠ B = 90°;
结论:直角三角形的两锐角互余.
问题1:在△ABC中,∠C=90°,求: ∠A+∠B的度数?由此你能得到什么结论?
问题2:在△ABC中,∠A+∠B=90°,则∠C度数为多少?由此你能得到什么结论?
解:在△ABC中,∵ ∠A + ∠B + ∠C = 180°;
又∵ ∠A + ∠B = 90°;
∴ ∠ C = 90°,即:△ABC是直角三角形;
结论:有两个角互余的三角形是直角三角形.
三角形内角和推论1:直角三角形的两锐角互余;
三角形内角和推论2:有两个角互余的三角形是直角三角形.
推论:像这样,由基本事实、定理直接得出的真命题叫做推论.
活动小结
1.在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A. 50° B. 45°
C. 40° D. 30°
A
2.在直角三角形中,有一个锐角是另一个锐角的2倍,则这两个锐角的度数是 和 .
30°
60°
3.已知:如图所示,△ABC中,∠AFB=135°,∠A、∠B的平分线AD、 BE交于F,试证明△ABC为直角三角形.
A
B
C
F
E
D
证明:∵在△AFB中,∠AFB=135°,(已知)
∴∠FAB+∠FBA=180°-135°=45°(三角形内角和定理)
∵AD、BE平分∠CAB、∠CBA,(已知)
∴∠CAB=2∠FAB,∠CBA=2∠FBA(角平分线的性质)
∴∠CAB+∠CBA=2(∠FAB+∠FBA)=90°,(等量代换)
∴△ABC为直角三角形.(有两个角互余的三角形是直角三角形)
证法
推论
转化为一个平角
或同旁内角互补
三角形的内角和等于180 °
作辅助线
转化思想
1.直角三角形的两个锐角互余.
2.有两个角互余的三角形是直角三角形.
针对本课关键词“三角形内角和定理的证明及推论”,说说你学到了什么.
