12.3 一次函数与二元一次方程 第2课时 课件 (共17张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 12.3 一次函数与二元一次方程 第2课时 课件 (共17张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:45:13 | ||
图片预览





文档简介
(共17张PPT)
第十二章 一次函数
12.3 一次函数与二元一次方程
12.3.2 一次函数与二元一次方程组
1. 会用图象法解二元一次方程组;
2.通过一次函数的图象,了解二元一次方程组解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
任务一:用图象法解二元一次方程组.
活动1:小组合作讨论,完成下列问题.
问题2:请在同一直角坐标系内分别画出函数y=-x+5与y=2x-1的图象,找出它们的交点坐标,并比较与上述方程的解有什么联系.
问题1:解方程组
解:利用消元法,解方程组得
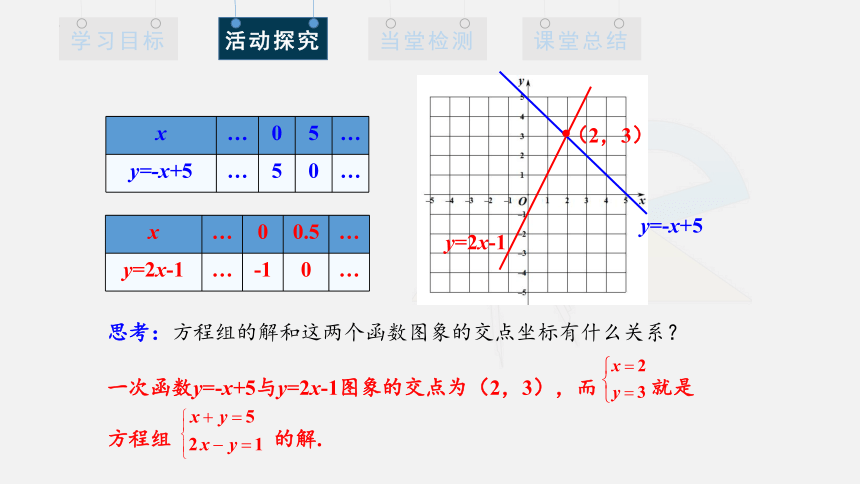
思考:方程组的解和这两个函数图象的交点坐标有什么关系?
y=-x+5
(2,3)
·
x … 0 5 …
y=-x+5 … 5 0 …
x … 0 0.5 …
y=2x-1 … -1 0 …
y=2x-1
一次函数y=-x+5与y=2x-1图象的交点为(2,3),而 就是
方程组 的解.
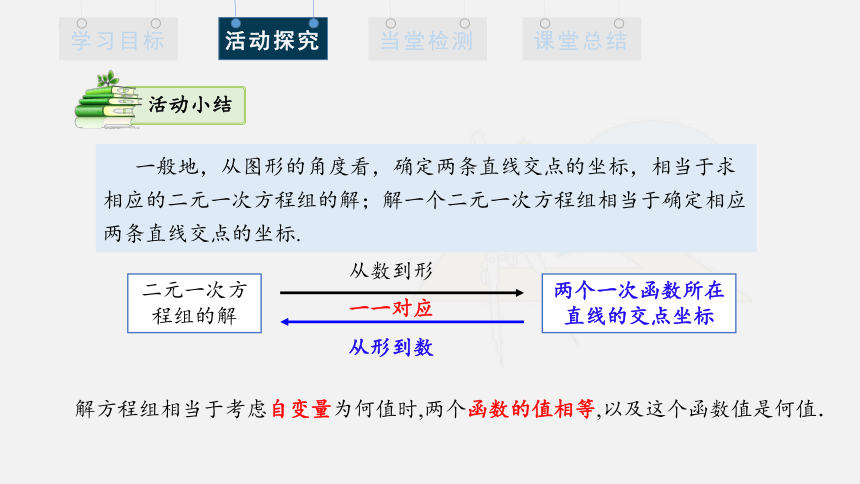
两个一次函数所在直线的交点坐标
二元一次方程组的解
从形到数
从数到形
一一对应
解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值.
活动小结
一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标.
练一练
若关于x,y的二元一次方程组 的解为 ,一次函数y=kx+b与y=mx+n的图象的交点坐标为( )
A
A.(1,2) B.(2,1) C.(2,3) D.(1,3)
用作图象的方法解方程组:
活动2:
解:由x-2y=-2可得:
同理,由2x–y=2可得y=2x – 2,在同坐标系中作出一次函数: 的图象和y=2x – 2的图象.
观察图象,得两直线交于点(2,2),所以方程组
的解是
思考:你能归纳运用图象法解二元一次方程组的一般步骤吗?
一般步骤
①方程化成函数
②画出函数图象
③找出图象的交点坐标
④写出方程组的解
①
②
①
②
任务二:通过一次函数的图像,了解二元一次方程组解的情形.
活动:已知方程组的图象,利用图象法说出下面两个方程组的解.
无解,两个一次函数图象平行.
无数解,两个一次函数图象重合.
活动小结
只有一组解(两直线相交)
有无穷多组解(两直线重合)
无解(两直线平行)
二元一次方程组
任务三:根据二元一次方程的系数判断解的情况.
活动:和同伴一起交流,回答下列问题.
问题:比较一下每例中两个方程x的系数之比、y的系数之比以及常数项之比,从中你发现怎样的规律?
上述活动直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
①当 a1:a2 ≠b1:b2 时 ,两直线相交,故方程组有唯一解;
②当 a1:a2=b1:b2 =c1 :c2时,两直线重合,故方程组有无穷组解;
③当a1:a2=b1:b2 ≠c1 :c2时,两直线平行,故方程组无解.
活动小结
3x+5y=8
2x-3y=7
既不解方程组也不画图,你能判断下列方程组的解的情况吗?
(1)
(2)
(3)
(4)
y=2x-3
4x-2y=6
3x-4y=5
6x-8y=12
2x+3y=5
y=x
一组解
无穷组解
无解
一组解
练一练
1.已知直线 y=-x+4 与 y=x+2 的图象如图,则方程组
的解为( )
y=-x+4
y=x+2
A.
B.
C.
D.
x=3
y=1
x=1
y=3
x=0
y=4
x=4
y=0
B
1
2
1
3
5
4
2
3
B
解析:二元一次方程组的解一般是指二元一次方程组的两个方程的公共解,也是两个一次函数所在直线的交点坐标.选项B中两直线平行,方程组无解,故选B项.
2.不解方程,下列方程组中无解的是( )
A. B.
C. D.
解:直线 与直线y=2x+7的交点坐标为(﹣2,3),所以原方程组的解为
3.利用函数图像解方程组:
针对本课关键词“一次函数与二元一次方程组”,说说你学到了什么?
第十二章 一次函数
12.3 一次函数与二元一次方程
12.3.2 一次函数与二元一次方程组
1. 会用图象法解二元一次方程组;
2.通过一次函数的图象,了解二元一次方程组解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
任务一:用图象法解二元一次方程组.
活动1:小组合作讨论,完成下列问题.
问题2:请在同一直角坐标系内分别画出函数y=-x+5与y=2x-1的图象,找出它们的交点坐标,并比较与上述方程的解有什么联系.
问题1:解方程组
解:利用消元法,解方程组得
思考:方程组的解和这两个函数图象的交点坐标有什么关系?
y=-x+5
(2,3)
·
x … 0 5 …
y=-x+5 … 5 0 …
x … 0 0.5 …
y=2x-1 … -1 0 …
y=2x-1
一次函数y=-x+5与y=2x-1图象的交点为(2,3),而 就是
方程组 的解.
两个一次函数所在直线的交点坐标
二元一次方程组的解
从形到数
从数到形
一一对应
解方程组相当于考虑自变量为何值时,两个函数的值相等,以及这个函数值是何值.
活动小结
一般地,从图形的角度看,确定两条直线交点的坐标,相当于求相应的二元一次方程组的解;解一个二元一次方程组相当于确定相应两条直线交点的坐标.
练一练
若关于x,y的二元一次方程组 的解为 ,一次函数y=kx+b与y=mx+n的图象的交点坐标为( )
A
A.(1,2) B.(2,1) C.(2,3) D.(1,3)
用作图象的方法解方程组:
活动2:
解:由x-2y=-2可得:
同理,由2x–y=2可得y=2x – 2,在同坐标系中作出一次函数: 的图象和y=2x – 2的图象.
观察图象,得两直线交于点(2,2),所以方程组
的解是
思考:你能归纳运用图象法解二元一次方程组的一般步骤吗?
一般步骤
①方程化成函数
②画出函数图象
③找出图象的交点坐标
④写出方程组的解
①
②
①
②
任务二:通过一次函数的图像,了解二元一次方程组解的情形.
活动:已知方程组的图象,利用图象法说出下面两个方程组的解.
无解,两个一次函数图象平行.
无数解,两个一次函数图象重合.
活动小结
只有一组解(两直线相交)
有无穷多组解(两直线重合)
无解(两直线平行)
二元一次方程组
任务三:根据二元一次方程的系数判断解的情况.
活动:和同伴一起交流,回答下列问题.
问题:比较一下每例中两个方程x的系数之比、y的系数之比以及常数项之比,从中你发现怎样的规律?
上述活动直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
①当 a1:a2 ≠b1:b2 时 ,两直线相交,故方程组有唯一解;
②当 a1:a2=b1:b2 =c1 :c2时,两直线重合,故方程组有无穷组解;
③当a1:a2=b1:b2 ≠c1 :c2时,两直线平行,故方程组无解.
活动小结
3x+5y=8
2x-3y=7
既不解方程组也不画图,你能判断下列方程组的解的情况吗?
(1)
(2)
(3)
(4)
y=2x-3
4x-2y=6
3x-4y=5
6x-8y=12
2x+3y=5
y=x
一组解
无穷组解
无解
一组解
练一练
1.已知直线 y=-x+4 与 y=x+2 的图象如图,则方程组
的解为( )
y=-x+4
y=x+2
A.
B.
C.
D.
x=3
y=1
x=1
y=3
x=0
y=4
x=4
y=0
B
1
2
1
3
5
4
2
3
B
解析:二元一次方程组的解一般是指二元一次方程组的两个方程的公共解,也是两个一次函数所在直线的交点坐标.选项B中两直线平行,方程组无解,故选B项.
2.不解方程,下列方程组中无解的是( )
A. B.
C. D.
解:直线 与直线y=2x+7的交点坐标为(﹣2,3),所以原方程组的解为
3.利用函数图像解方程组:
针对本课关键词“一次函数与二元一次方程组”,说说你学到了什么?
