13.2 命题与证明 第2课时课件(共14张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 13.2 命题与证明 第2课时课件(共14张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.2 证明
1.理解基本事实、定理、证明的意义.
2.了解证明的基本步骤和书写格式,能运用已学过的几何知识证明一些简单的几何问题.
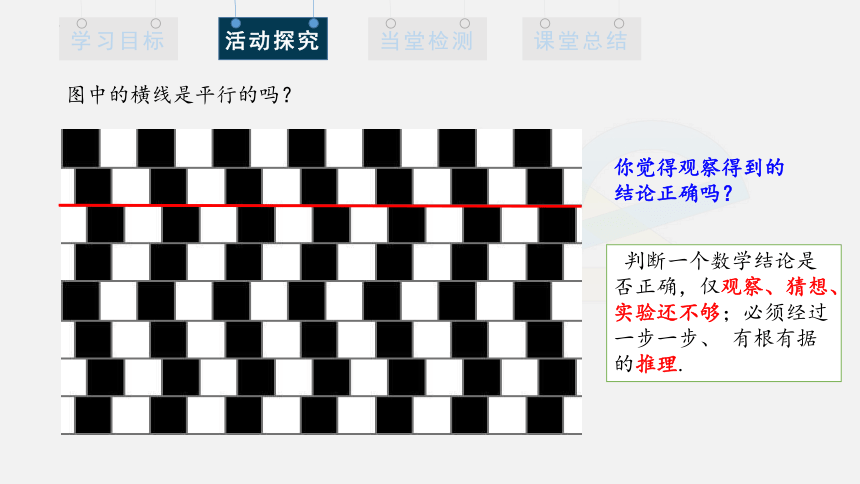
图中的横线是平行的吗?
你觉得观察得到的结论正确吗?
判断一个数学结论是否正确,仅观察、猜想、实验还不够;必须经过一步一步、 有根有据的推理.
基本事实:人们从长期的实践中总结出来,作为判断其他命题真假的依据,这些作为原始依据的真命题叫做公理.
定理:从公理或其他真命题出发,用推理方法证明为正确的、并进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
基本事实和定理有什么共同点和不同点?
共同点:都是真命题;
不同点:基本事实的正确性是人们长期实践检验所证实的,不需要证明;定理的正确性是依赖推理证实的.
任务一:理解基本事实、定理、证明的意义.
活动:小组合作讨论,回答下列问题.
问题1:你能举出几个前面已学过的基本事实吗?
问题2:回顾我们学过的命题,有哪些是定理?
问题1:关于直线:两点确定一条直线;
关于平行:经过直线外一点,有且只有一条直线平行于已知直线;
关于线段:两点之间,线段最短;
关于等式:如果a = b,那么a + c = b + c.
平行线判定定理:内错角相等,两直线平行;
平行线性质定理:两直线平行,内错角相等;
三角形内角和定理:三角形内角和等于180°;
问题2:回顾我们学过的命题,有哪些是定理?
定理:通过真命题(公理或其他已被证明的定理)出发,经过演绎推导,被证明为正确的结论的命题或公式.
思考:下列命题中,哪些正确,哪些错误?和同伴一起交流.
(1)每一个月都有31天;
(2)同位角相等;
(3)同角的补角相等.
错误
错误
正确
你能说说你是怎么判断的吗?
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑规则,推导出结论,这一方法称为演绎推理(或演绎法).
演绎推理的过程,就是演绎证明,简称证明.
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
基本事实或公理
一些条件
+
活动小结
任务二:了解证明的基本步骤和书写格式.
活动:小组合作讨论,完成下列问题.
如图,直线c与直线a,b相交,且∠1=∠2,求证:a∥b.
证明:∵∠1=∠2(已知),
∵∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴a∥b(同位角相等,两直线平行).
3
2
1
a
b
c
注:符号“∵”读作“因为”;符号“∴”读作“所以”.
活动小结
证明的基本步骤与书写格式总结:
证明步骤:已知条件 → 依据公理、已证定理 → 结论
书写格式:证明:∵ ( 已知条件 );
∴ ( 中间推论 );
∴ ( 结论 ).
1.下列问题用到推理的是( )
A. 根据a=10,b=10,得到a=b
B. 观察得到了三角形有三个角
C. 老师告诉了我们关于金字塔的许多奥秘
D. 由经验可知过两点有且只有一条直线
A
2.在下面各题的括号内,填上推理的依据.
(1)已知,如图:∠1=∠B,求证:∠2=∠C.
A
B
C
D
E
1
2
证明:∵∠1=∠B,( )
∴ AE∥BC. ( )
∴ ∠2 =∠C.( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
(2)已知:如图,∠1=∠2.求证:AB∥CD.
证明:
∵∠1=∠2,( )
∴AD∥BC,( )
∴∠1=∠3. ( )
等量代换
已知
同位角相等,两直线平行
又∵∠2=∠3,( )
1
3
2
a
b
c
对顶角相等
针对本课关键词“证明”,说说你学到了什么?
证明
定理:经过证明的真命题称为定理.
证明:推理的过程称为证明.
第十三章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.2 证明
1.理解基本事实、定理、证明的意义.
2.了解证明的基本步骤和书写格式,能运用已学过的几何知识证明一些简单的几何问题.
图中的横线是平行的吗?
你觉得观察得到的结论正确吗?
判断一个数学结论是否正确,仅观察、猜想、实验还不够;必须经过一步一步、 有根有据的推理.
基本事实:人们从长期的实践中总结出来,作为判断其他命题真假的依据,这些作为原始依据的真命题叫做公理.
定理:从公理或其他真命题出发,用推理方法证明为正确的、并进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
基本事实和定理有什么共同点和不同点?
共同点:都是真命题;
不同点:基本事实的正确性是人们长期实践检验所证实的,不需要证明;定理的正确性是依赖推理证实的.
任务一:理解基本事实、定理、证明的意义.
活动:小组合作讨论,回答下列问题.
问题1:你能举出几个前面已学过的基本事实吗?
问题2:回顾我们学过的命题,有哪些是定理?
问题1:关于直线:两点确定一条直线;
关于平行:经过直线外一点,有且只有一条直线平行于已知直线;
关于线段:两点之间,线段最短;
关于等式:如果a = b,那么a + c = b + c.
平行线判定定理:内错角相等,两直线平行;
平行线性质定理:两直线平行,内错角相等;
三角形内角和定理:三角形内角和等于180°;
问题2:回顾我们学过的命题,有哪些是定理?
定理:通过真命题(公理或其他已被证明的定理)出发,经过演绎推导,被证明为正确的结论的命题或公式.
思考:下列命题中,哪些正确,哪些错误?和同伴一起交流.
(1)每一个月都有31天;
(2)同位角相等;
(3)同角的补角相等.
错误
错误
正确
你能说说你是怎么判断的吗?
从已知条件出发,依据定义、基本事实、已证定理,并按照逻辑规则,推导出结论,这一方法称为演绎推理(或演绎法).
演绎推理的过程,就是演绎证明,简称证明.
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
基本事实或公理
一些条件
+
活动小结
任务二:了解证明的基本步骤和书写格式.
活动:小组合作讨论,完成下列问题.
如图,直线c与直线a,b相交,且∠1=∠2,求证:a∥b.
证明:∵∠1=∠2(已知),
∵∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴a∥b(同位角相等,两直线平行).
3
2
1
a
b
c
注:符号“∵”读作“因为”;符号“∴”读作“所以”.
活动小结
证明的基本步骤与书写格式总结:
证明步骤:已知条件 → 依据公理、已证定理 → 结论
书写格式:证明:∵ ( 已知条件 );
∴ ( 中间推论 );
∴ ( 结论 ).
1.下列问题用到推理的是( )
A. 根据a=10,b=10,得到a=b
B. 观察得到了三角形有三个角
C. 老师告诉了我们关于金字塔的许多奥秘
D. 由经验可知过两点有且只有一条直线
A
2.在下面各题的括号内,填上推理的依据.
(1)已知,如图:∠1=∠B,求证:∠2=∠C.
A
B
C
D
E
1
2
证明:∵∠1=∠B,( )
∴ AE∥BC. ( )
∴ ∠2 =∠C.( )
已知
同位角相等,两直线平行
两直线平行,内错角相等
(2)已知:如图,∠1=∠2.求证:AB∥CD.
证明:
∵∠1=∠2,( )
∴AD∥BC,( )
∴∠1=∠3. ( )
等量代换
已知
同位角相等,两直线平行
又∵∠2=∠3,( )
1
3
2
a
b
c
对顶角相等
针对本课关键词“证明”,说说你学到了什么?
证明
定理:经过证明的真命题称为定理.
证明:推理的过程称为证明.
