14.2 三角形全等的判定 第1课时 课件 (共17张PPT)沪科版八年级数学上册
文档属性
| 名称 | 14.2 三角形全等的判定 第1课时 课件 (共17张PPT)沪科版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:45:45 | ||
图片预览




文档简介
(共17张PPT)
第十四章 全等三角形
14.2 三角形全等的判定
14.2.1 三角形全等的判定“SAS”
1.知道要判定两个三角形全等至少需要三个元素.
2.掌握三角形全等的“边角边”判定方法.
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,
老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等,
一定要知道三角旗所有的边长和所有的角度吗?
思考:至少要满足几个条件,才能保证三角旗全等
任务一:探索判定三角形全等的元素.
活动:三角形有六个基本元素(三条边和三个角),只给定其中的一个元素或两个元素,能否确定一个三角形的形状和大小?
通过画图,说明你的判断.
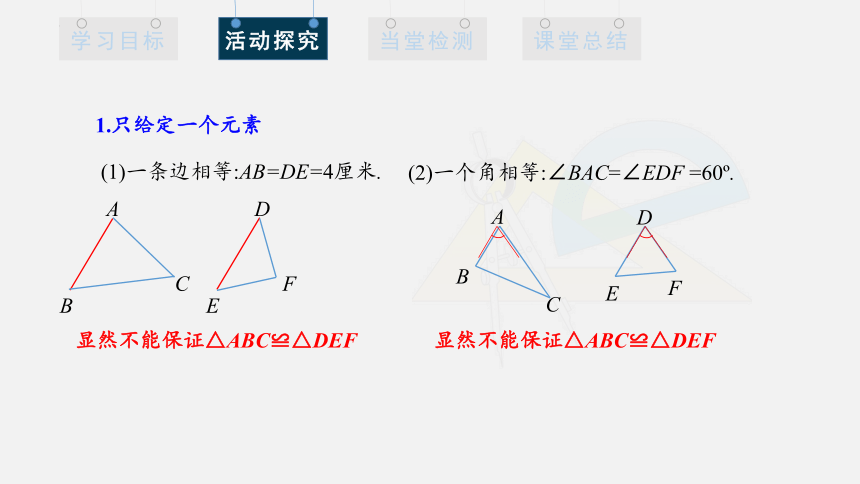
1.只给定一个元素:
(1)一条边长为4厘米;
(2)一个角为60 .
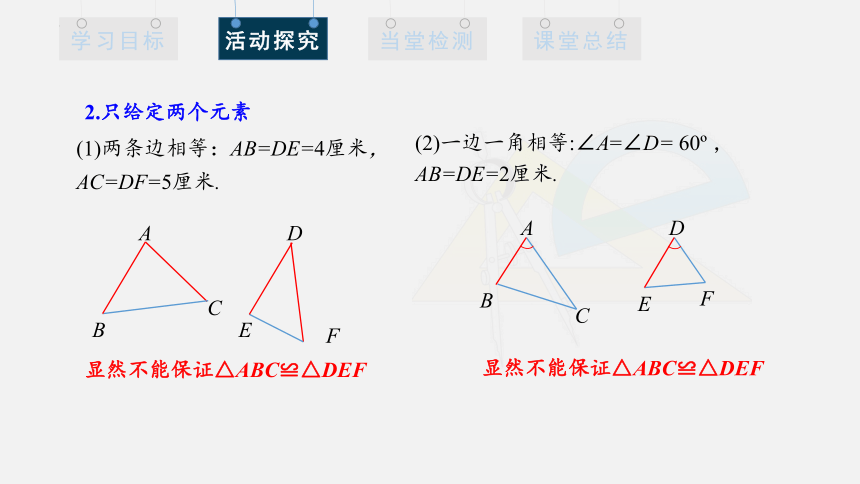
2.只给定两个元素:
(1)两条边长分别为4厘米、5厘米;
(2)一条边长为2厘米,一个角为60 ;
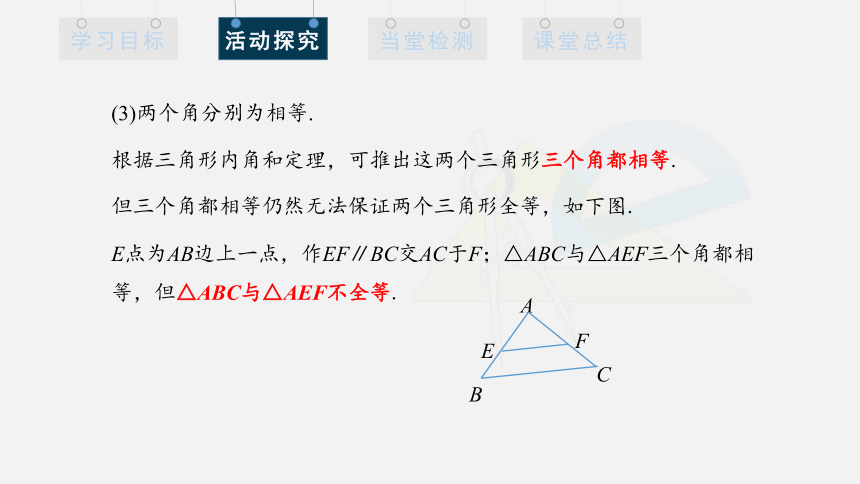
(3)两个角分别为相等.
1.只给定一个元素
(1)一条边相等:AB=DE=4厘米.
A
B
C
D
E
F
(2)一个角相等:∠BAC=∠EDF =60 .
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
显然不能保证△ABC≌△DEF
2.只给定两个元素
(1)两条边相等:AB=DE=4厘米,AC=DF=5厘米.
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
(2)一边一角相等:∠A=∠D= 60 ,
AB=DE=2厘米.
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
(3)两个角分别为相等.
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
E点为AB边上一点,作EF∥BC交AC于F;△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
A
B
C
E
F
活动小结
思考:确定三角形的形状、大小的条件能否作为判定三角形全等的条件呢?
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等.
任务二:掌握三角形全等的“边角边”的判定方法.
A
B
C
作法:1. 画∠MDN=∠BAC;
2. 在射线DM上截取DE=AB,在射线DN
上截取DF=AC;
3. 连接EF.
D
E
F
∴△ABC≌△DEF.
M
N
活动1:先任意画一个△ABC,再画一个△DEF.AB=DE,AC=DF,∠A=∠D.把画好的△DEF剪下来,放到△ABC上,判断它们是否全等.
“边角边”判定方法:两边和它们的夹角分别相等的两个三角形全等.(简写为“边角边”或“SAS”)
几何语言:在△ABC和△DEF中,
A
B
C
D
E
F
AB=DE,
∠A=∠D,
AC=DF,
∴ △ABC≌△DEF(SAS).
活动小结
必须是两边“夹角”
练一练
在下列图中找出全等三角形.
8cm
9cm
8cm
9cm
8cm
5cm
Ⅲ
8cm
8cm
8cm
5cm
(1)
(2)
(3)
(4)
(5)
解:全等三角形有:(1)和(4),(2)和(5).
30°
30°
30°
30°
30°
分析:如果能证明△ABC≌△DEC, 就可以得出AB=DE.由题意知,△ABC和△DEC具备“边角边”的条件.
E
D
C
B
A
1
2
活动2:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么
E
D
C
B
A
1
2
解:
AC=DC
∠1=∠2
BC=EC
∴△ACB≌△DCE(SAS).
在△ACB和△DCE中,
∴AB=DE.
故量出DE的长就是A、B的距离.
小结:因为全等三角形的对应边相等,对应角相等,所以证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
1.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,要用SAS证明△ABC≌△DEF,可以添加的条件是( )
A.∠A=∠D B.AC∥DF
C.BE=CF D.AC=DF
C
2. 如图,AC=BD,∠CAB =∠DBA,求证:BC=AD.
证明:在△ABC与△BAD中:AC=BD,
∠CAB=∠DBA,AB=BA;(已知)
∴ △ABC≌△BAD;(SAS)
∴ BC = AD.(全等三角形的对应边相等)
A
B
C
D
3.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.
求证:△AEF≌△BCD.
证明:∵AE∥BC,∴∠A=∠B.
∵AD=BF,∴AF=BD.
在△AEF和△BCD中,
AE=BC,
∵ ∠A=∠B,
AF=BD,
∴△AEF≌△BCD(SAS).
边角边
内容
“SAS”
注意
1.已知两边,必须找“夹角”
2. 已知一角和这角的一夹边,必须找这角的另一夹边
应用
证明线段 (或角相等)
说一说你本堂课都学到了哪些知识?
第十四章 全等三角形
14.2 三角形全等的判定
14.2.1 三角形全等的判定“SAS”
1.知道要判定两个三角形全等至少需要三个元素.
2.掌握三角形全等的“边角边”判定方法.
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,
老师应提供多少个数据才能保证同学们制作出来的三角形彩旗全等,
一定要知道三角旗所有的边长和所有的角度吗?
思考:至少要满足几个条件,才能保证三角旗全等
任务一:探索判定三角形全等的元素.
活动:三角形有六个基本元素(三条边和三个角),只给定其中的一个元素或两个元素,能否确定一个三角形的形状和大小?
通过画图,说明你的判断.
1.只给定一个元素:
(1)一条边长为4厘米;
(2)一个角为60 .
2.只给定两个元素:
(1)两条边长分别为4厘米、5厘米;
(2)一条边长为2厘米,一个角为60 ;
(3)两个角分别为相等.
1.只给定一个元素
(1)一条边相等:AB=DE=4厘米.
A
B
C
D
E
F
(2)一个角相等:∠BAC=∠EDF =60 .
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
显然不能保证△ABC≌△DEF
2.只给定两个元素
(1)两条边相等:AB=DE=4厘米,AC=DF=5厘米.
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
(2)一边一角相等:∠A=∠D= 60 ,
AB=DE=2厘米.
A
B
C
D
E
F
显然不能保证△ABC≌△DEF
(3)两个角分别为相等.
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
E点为AB边上一点,作EF∥BC交AC于F;△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
A
B
C
E
F
活动小结
思考:确定三角形的形状、大小的条件能否作为判定三角形全等的条件呢?
结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等.
任务二:掌握三角形全等的“边角边”的判定方法.
A
B
C
作法:1. 画∠MDN=∠BAC;
2. 在射线DM上截取DE=AB,在射线DN
上截取DF=AC;
3. 连接EF.
D
E
F
∴△ABC≌△DEF.
M
N
活动1:先任意画一个△ABC,再画一个△DEF.AB=DE,AC=DF,∠A=∠D.把画好的△DEF剪下来,放到△ABC上,判断它们是否全等.
“边角边”判定方法:两边和它们的夹角分别相等的两个三角形全等.(简写为“边角边”或“SAS”)
几何语言:在△ABC和△DEF中,
A
B
C
D
E
F
AB=DE,
∠A=∠D,
AC=DF,
∴ △ABC≌△DEF(SAS).
活动小结
必须是两边“夹角”
练一练
在下列图中找出全等三角形.
8cm
9cm
8cm
9cm
8cm
5cm
Ⅲ
8cm
8cm
8cm
5cm
(1)
(2)
(3)
(4)
(5)
解:全等三角形有:(1)和(4),(2)和(5).
30°
30°
30°
30°
30°
分析:如果能证明△ABC≌△DEC, 就可以得出AB=DE.由题意知,△ABC和△DEC具备“边角边”的条件.
E
D
C
B
A
1
2
活动2:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离,为什么
E
D
C
B
A
1
2
解:
AC=DC
∠1=∠2
BC=EC
∴△ACB≌△DCE(SAS).
在△ACB和△DCE中,
∴AB=DE.
故量出DE的长就是A、B的距离.
小结:因为全等三角形的对应边相等,对应角相等,所以证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.
1.如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE,要用SAS证明△ABC≌△DEF,可以添加的条件是( )
A.∠A=∠D B.AC∥DF
C.BE=CF D.AC=DF
C
2. 如图,AC=BD,∠CAB =∠DBA,求证:BC=AD.
证明:在△ABC与△BAD中:AC=BD,
∠CAB=∠DBA,AB=BA;(已知)
∴ △ABC≌△BAD;(SAS)
∴ BC = AD.(全等三角形的对应边相等)
A
B
C
D
3.如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.
求证:△AEF≌△BCD.
证明:∵AE∥BC,∴∠A=∠B.
∵AD=BF,∴AF=BD.
在△AEF和△BCD中,
AE=BC,
∵ ∠A=∠B,
AF=BD,
∴△AEF≌△BCD(SAS).
边角边
内容
“SAS”
注意
1.已知两边,必须找“夹角”
2. 已知一角和这角的一夹边,必须找这角的另一夹边
应用
证明线段 (或角相等)
说一说你本堂课都学到了哪些知识?
