13.1 三角形中的边角关系 第2课时 课件(共15张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 13.1 三角形中的边角关系 第2课时 课件(共15张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
13.1.2 三角形中角的关系
1.会按角对三角形进行分类;
2.掌握三角形内角和定理;
3.能用三角形内角和定理解决相关问题.
三角形若按角来分类,可分为哪几类?
三角形按边长关系,可分为:
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
思考
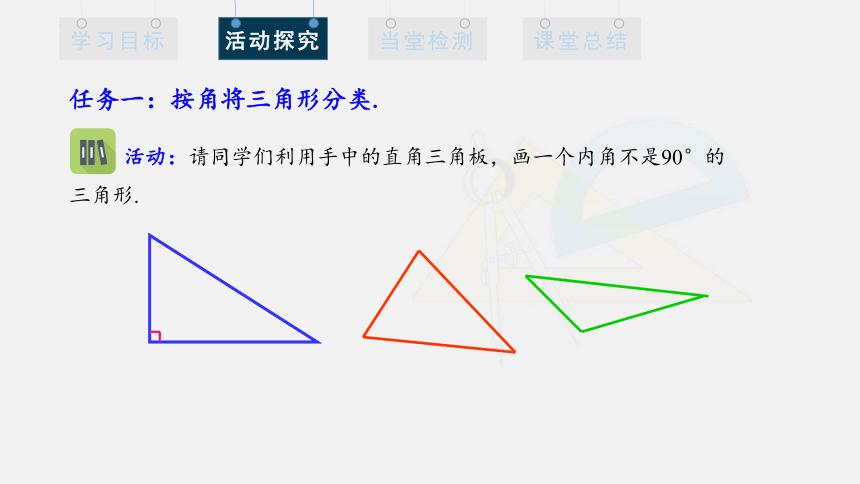
任务一:按角将三角形分类.
活动:请同学们利用手中的直角三角板,画一个内角不是90°的
三角形.
直角边
直角边
斜边
A
B
C
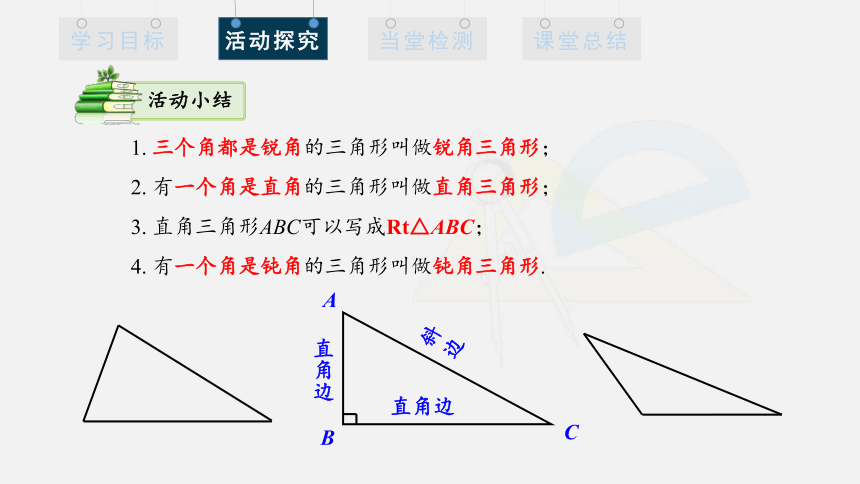
活动小结
1. 三个角都是锐角的三角形叫做锐角三角形;
2. 有一个角是直角的三角形叫做直角三角形;
3. 直角三角形ABC可以写成Rt△ABC;
4. 有一个角是钝角的三角形叫做钝角三角形.
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形
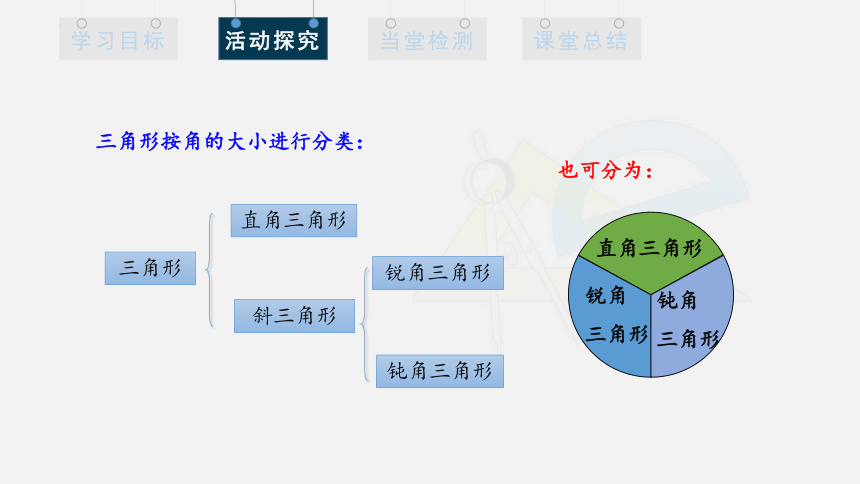
三角形按角的大小进行分类:
直角三角形
锐角
三角形
钝角
三角形
也可分为:
如图,∠ACB=90 °, CD⊥AB,垂足是D.写出图中
所有直角三角形,并指出它们的斜边.
A
B
C
D
解:直角三角形有:(1)Rt△ABC,斜边为AB;
(2)Rt△ACD,斜边为AC;
(3)Rt△BCD,斜边为BC.
练一练
任务二:掌握三角形内角和定理.
活动1:和同伴一起交流,完成下列问题.
问题:(1)在一个三角形中,三个内角有什么关系?
(2)在小学,我们曾用折叠、剪拼或用量角器度量的方法研究过这个问题,你还记得有什么结论吗?
折叠
拼接
活动小结
则有:∠A+∠B+∠C=180°.
已知:△ABC.
三角形内角和定理:三角形的内角和等于180°.
活动2:如图,CE⊥AF,垂足为E,CE与BF相交于点D,
∠F=45°,∠FBA=75°, 求∠C的度数.
A
B
C
D
E
F
解:因为∠F=45°,∠FBA=75°,
所以在△AFB中,∠A=180°-75°-45°=60°,
又因为CE⊥AF,
所以△ACE中,∠C=180°-90°-60°=30°.
如图,由三角形的内角和定理易推得∠1+∠2=∠3+∠4.
1
2
4
3
1
2
4
3
2
3
活动小结
1.填空.
(1)在△ABC中,∠A=35°,∠B=40 °,则△ABC是 三角形.
(2)在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
钝角
直角
2.求出下列各图中的x值.
x=70
x=60
x=30
x=50
3.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:因为∠A+∠ADE=180°,
所以AB∥DE,所以∠CED=∠B=78°.
又因为∠C=60°,
所以∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)=42°.
针对本课关键词“三角形中角的关系”,说说你学到了什么?
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
第十三章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
13.1.2 三角形中角的关系
1.会按角对三角形进行分类;
2.掌握三角形内角和定理;
3.能用三角形内角和定理解决相关问题.
三角形若按角来分类,可分为哪几类?
三角形按边长关系,可分为:
等腰三角形(等边三角形是它的特例)
不等边三角形
三角形
思考
任务一:按角将三角形分类.
活动:请同学们利用手中的直角三角板,画一个内角不是90°的
三角形.
直角边
直角边
斜边
A
B
C
活动小结
1. 三个角都是锐角的三角形叫做锐角三角形;
2. 有一个角是直角的三角形叫做直角三角形;
3. 直角三角形ABC可以写成Rt△ABC;
4. 有一个角是钝角的三角形叫做钝角三角形.
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形
三角形按角的大小进行分类:
直角三角形
锐角
三角形
钝角
三角形
也可分为:
如图,∠ACB=90 °, CD⊥AB,垂足是D.写出图中
所有直角三角形,并指出它们的斜边.
A
B
C
D
解:直角三角形有:(1)Rt△ABC,斜边为AB;
(2)Rt△ACD,斜边为AC;
(3)Rt△BCD,斜边为BC.
练一练
任务二:掌握三角形内角和定理.
活动1:和同伴一起交流,完成下列问题.
问题:(1)在一个三角形中,三个内角有什么关系?
(2)在小学,我们曾用折叠、剪拼或用量角器度量的方法研究过这个问题,你还记得有什么结论吗?
折叠
拼接
活动小结
则有:∠A+∠B+∠C=180°.
已知:△ABC.
三角形内角和定理:三角形的内角和等于180°.
活动2:如图,CE⊥AF,垂足为E,CE与BF相交于点D,
∠F=45°,∠FBA=75°, 求∠C的度数.
A
B
C
D
E
F
解:因为∠F=45°,∠FBA=75°,
所以在△AFB中,∠A=180°-75°-45°=60°,
又因为CE⊥AF,
所以△ACE中,∠C=180°-90°-60°=30°.
如图,由三角形的内角和定理易推得∠1+∠2=∠3+∠4.
1
2
4
3
1
2
4
3
2
3
活动小结
1.填空.
(1)在△ABC中,∠A=35°,∠B=40 °,则△ABC是 三角形.
(2)在△ABC中,∠A:∠B:∠C=1:2:3,则△ABC是 三角形.
钝角
直角
2.求出下列各图中的x值.
x=70
x=60
x=30
x=50
3.如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:因为∠A+∠ADE=180°,
所以AB∥DE,所以∠CED=∠B=78°.
又因为∠C=60°,
所以∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)=42°.
针对本课关键词“三角形中角的关系”,说说你学到了什么?
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
