12.2 一次函数 第7课时课件(共15张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 12.2 一次函数 第7课时课件(共15张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:48:50 | ||
图片预览





文档简介
(共15张PPT)
第十二章 一次函数
12.2 一次函数
12.2.7 一次函数与方程、不等式
1.理解一次函数与一元一次方程、一元一次不等式的关系;
2.会用图像法求一元一次方程和一元一次不等式的解和解集.
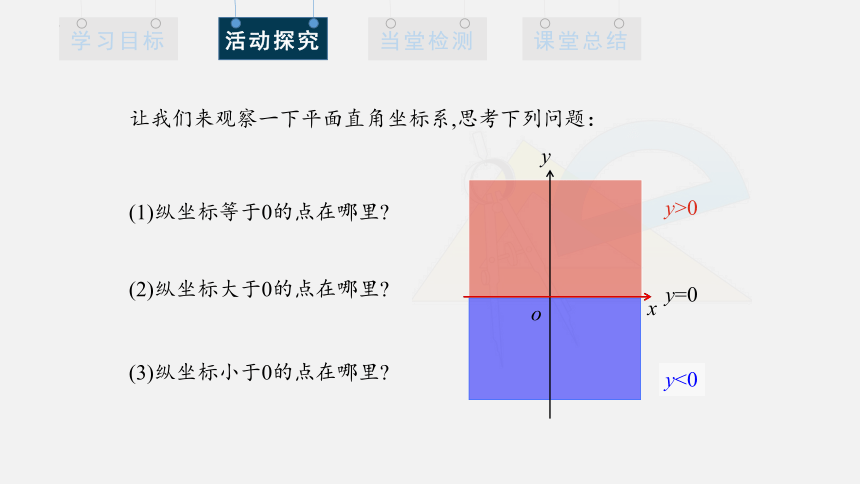
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于0的点在哪里
(2)纵坐标大于0的点在哪里
(3)纵坐标小于0的点在哪里
x
y
o
y=0
任务一:理解一次函数与一元一次方程的关系.
活动:独立思考,完成下列问题.
问题:(1)解方程2x+20=0;
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
2x=-20
x=-10
(2) 当y=0时 ,即
2x+20=0
2x=-20
x=-10
从“函数值”
角度看
两个问题实际上是同一个问题.
(3)画出函数 y=2x+20的图象,并确定它与x轴的交点坐标.
0
x
y
20
-10
y=2x+20
从“函数图象”上看
直线y=2x+20与x轴交点坐标为(____,_____),
这说明方程2x+20=0的解是x=_____.
-10
0
-10
思考
活动小结
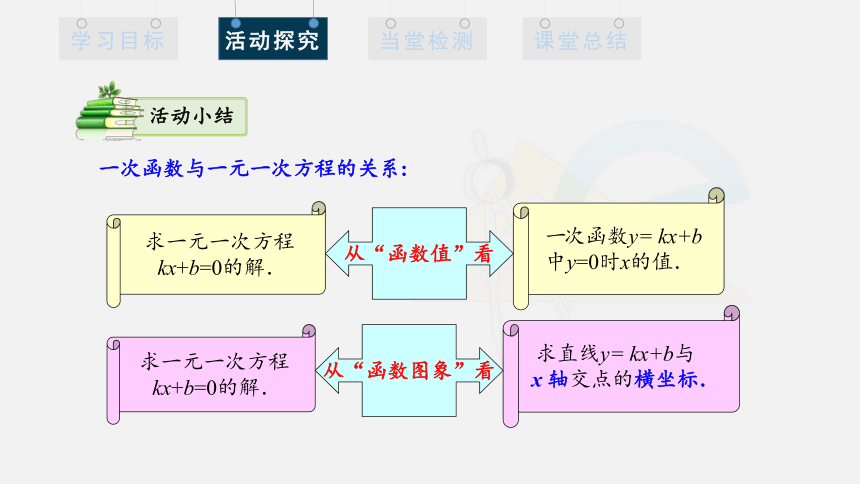
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系:
一次函数y= kx+b
中y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b与
x 轴交点的横坐标.
从“函数图象”看
练一练
直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=________.
解析:直线y=2x+b与x轴的交点坐标是(2,0),
则x=2时,y=0,关于x的方程2x+b=0的解是x=2.
2
方法总结:直线y=kx+b与x轴交点的横坐标就是方程kx+b=0的解,反之亦然.所以在解题时,常需作出一次函数的草图,结合图形分析更加直观、方便.
任务二:用图象法求一元一次不等式的解和解集.
活动:观察函数y=2x+6在x轴上方的函数图象所对应的函数值y和自变量x的取值范围.
解析:观察函数图象,经过点A(0,6),
B(-3,0),函数y=2x+6在x轴上方时,
函数值y>0,自变量x>-3.
思考:它们与不等式2x+6>0及其解集有何关系?
两者实际上是同一个问题,可以看作求不等式2x+6>0的解集.
问题1:你能通过观察函数图象得出一次不等式2x+6<0的解集吗?
x< -3
y=2x+6
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
问题2:请同学们观察一次函数y=2x+6和y=3的图象,你能说出2x+6=3的解和2x+6>3的解集吗?
y=2x+6
y=3
-1.5
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
x=-1.5
x>-1.5
一次函数与一元一次不等式的关系:
从“函数值”看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
y=kx+b的值
大于(或小于)0时,
x的取值范围
求kx+b>0(或<0)
(k≠0)的解集
活动小结
若直线y=kx+3经过点A ,则不等式kx+3≥0的解集是( )
A. B.
C. D.
B
练一练
1.已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2.已知:一次函数y=kx-5与x轴的交点为(3,0),那么你能说出kx-5=0的解吗?
3.已知关于x的一元一次方程mx+n=0的解是-3,则直线y=mx+n与x轴的交点坐标是_______.
x=2.5
x=3
(-3,0)
4.画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集; (2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于
x轴下方的x的取值范围,即x>2;
(2)由图象可知,当x>1时,y<3.
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
针对本课关键词“一次函数与一元一次方程、一元一次不等式”,
说说你学到了什么?
第十二章 一次函数
12.2 一次函数
12.2.7 一次函数与方程、不等式
1.理解一次函数与一元一次方程、一元一次不等式的关系;
2.会用图像法求一元一次方程和一元一次不等式的解和解集.
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于0的点在哪里
(2)纵坐标大于0的点在哪里
(3)纵坐标小于0的点在哪里
x
y
o
y=0
任务一:理解一次函数与一元一次方程的关系.
活动:独立思考,完成下列问题.
问题:(1)解方程2x+20=0;
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
2x=-20
x=-10
(2) 当y=0时 ,即
2x+20=0
2x=-20
x=-10
从“函数值”
角度看
两个问题实际上是同一个问题.
(3)画出函数 y=2x+20的图象,并确定它与x轴的交点坐标.
0
x
y
20
-10
y=2x+20
从“函数图象”上看
直线y=2x+20与x轴交点坐标为(____,_____),
这说明方程2x+20=0的解是x=_____.
-10
0
-10
思考
活动小结
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系:
一次函数y= kx+b
中y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b与
x 轴交点的横坐标.
从“函数图象”看
练一练
直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=________.
解析:直线y=2x+b与x轴的交点坐标是(2,0),
则x=2时,y=0,关于x的方程2x+b=0的解是x=2.
2
方法总结:直线y=kx+b与x轴交点的横坐标就是方程kx+b=0的解,反之亦然.所以在解题时,常需作出一次函数的草图,结合图形分析更加直观、方便.
任务二:用图象法求一元一次不等式的解和解集.
活动:观察函数y=2x+6在x轴上方的函数图象所对应的函数值y和自变量x的取值范围.
解析:观察函数图象,经过点A(0,6),
B(-3,0),函数y=2x+6在x轴上方时,
函数值y>0,自变量x>-3.
思考:它们与不等式2x+6>0及其解集有何关系?
两者实际上是同一个问题,可以看作求不等式2x+6>0的解集.
问题1:你能通过观察函数图象得出一次不等式2x+6<0的解集吗?
x< -3
y=2x+6
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
问题2:请同学们观察一次函数y=2x+6和y=3的图象,你能说出2x+6=3的解和2x+6>3的解集吗?
y=2x+6
y=3
-1.5
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
x=-1.5
x>-1.5
一次函数与一元一次不等式的关系:
从“函数值”看
求kx+b>0(或<0)
(k≠0)的解集
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
y=kx+b的值
大于(或小于)0时,
x的取值范围
求kx+b>0(或<0)
(k≠0)的解集
活动小结
若直线y=kx+3经过点A ,则不等式kx+3≥0的解集是( )
A. B.
C. D.
B
练一练
1.已知:一次函数y=0.8x-2与x轴的交点为(2.5,0),你能说出0.8x-2=0的解吗?
2.已知:一次函数y=kx-5与x轴的交点为(3,0),那么你能说出kx-5=0的解吗?
3.已知关于x的一元一次方程mx+n=0的解是-3,则直线y=mx+n与x轴的交点坐标是_______.
x=2.5
x=3
(-3,0)
4.画出函数y=-3x+6的图象,结合图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集; (2)当x取何值时,y<3
解:作出函数y=-3x+6的图象,如图所示,图象与x轴交于点B(2,0).
(1)由图象可知,不等式-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于
x轴下方的x的取值范围,即x>2;
(2)由图象可知,当x>1时,y<3.
x
O
B(2,0)
A(0,6)
3
1
(1,3)
y
针对本课关键词“一次函数与一元一次方程、一元一次不等式”,
说说你学到了什么?
