12.2 一次函数 第6课时课件(共15张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 12.2 一次函数 第6课时课件(共15张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:51:15 | ||
图片预览






文档简介
(共15张PPT)
第十二章 一次函数
12.2 一次函数
12.2.6 方案选择问题
1.了解一次函数的应用价值;
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.
任务:利用一次函数进行方案决策.
活动1:小组合作讨论,完成下列问题.
情境:学校准备去白云山春游,甲、乙两家旅行社原价都是每人100元,都表示对学生有优惠,甲旅行社表示:全部8折收费,乙旅行社表示学校先交1000元后,给予每位游客6折优惠.
问题1:设学生人数为x,甲、乙两旅行社实际收取总费用为y1,y2(元),试分别列出y1,y2与x的函数关系式.
问题2:讨论应选择哪家旅行社较优惠.你能想出多少种方法?
解:y1= 80x,
y2= 60x+1000.
解析:根据两家的收费标准,列出函数即可解决问题;
问题1:设学生人数为x,甲、乙两旅行社实际收取总费用为y1,y2(元),试分别列出y1,y2与x的函数关系式.
问题2:讨论应选择哪家旅行社较优惠.你能想出多少种解法?
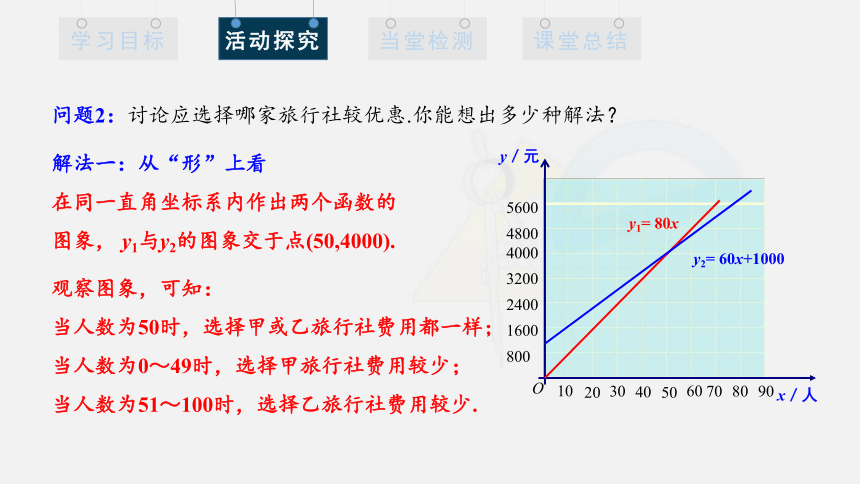
解法一:从“形”上看
在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49时,选择甲旅行社费用较少;
当人数为51~100时,选择乙旅行社费用较少.
解法二:从“数”上看
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49时,选择甲旅行社费用较少.
解法三:用作差法列出新的方程判断函数值与0的关系.
设选择甲、乙旅行社费用之差为y,则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0) 由图知:
(1)当x=50时,y=0,即y1=y2 ;
(2)当x>50时,y > 0,即y1 > y2 ;
(3)当x<50时,y <0,即y1 < y2 .
活动小结
应用一次函数选择最佳方案
1.从数学的角度分析实际问题,建立函数模型;
2.列出两个一次函数,比较函数值的大小关系;
3.结合实际需求,选择最佳方案.
活动2:小组合作讨论,回答下列问题.
情境:某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
问题2:试讨论A、B两地中,哪个的运费较少;
问题1:分别求出yA、yB与x之间的函数关系式;
问题3:考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
解:(1)yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
问题1:分别求出yA、yB与x之间的函数关系式;
问题2:试讨论A、B两地中,哪个的运费较少;
(2)因为yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
所以当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少.
问题3:考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
设两地运费之和为y元,则
y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
因为y随x的增大而减小,x最大为50,
所以y最小=-2×50+9680=9580.
在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元.
阅读理解题的解题关键是读懂题意.
第(2)小题比较大小要注意分类讨论,
第(3)小题是利用一次函数的方案设计问题,
一般先根据数量之间的关系建立函数,
然后再利用一次函数的增减性确定出符合要求的最佳方案.
活动小结
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A.方案A B.方案B
C.两种方案一样优惠 D.不能确定
B
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x千米计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元.若y1元、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( )
A.当月用车路程为2 000千米时,两家汽车租赁公司
租赁费用相同
B.当月用车路程为2 300千米时,租用乙汽车租赁
公司的车比较合算
C.除去月固定租赁费,甲汽车租赁公司每千米收取的费用比乙汽车租赁公司多
D.甲汽车租赁公司每月的固定租赁费高于乙汽车租赁公司
D
针对本课关键词“方案选择问题”,说说你学到了什么?
利用一次函数进行方案决策
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
第十二章 一次函数
12.2 一次函数
12.2.6 方案选择问题
1.了解一次函数的应用价值;
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.
任务:利用一次函数进行方案决策.
活动1:小组合作讨论,完成下列问题.
情境:学校准备去白云山春游,甲、乙两家旅行社原价都是每人100元,都表示对学生有优惠,甲旅行社表示:全部8折收费,乙旅行社表示学校先交1000元后,给予每位游客6折优惠.
问题1:设学生人数为x,甲、乙两旅行社实际收取总费用为y1,y2(元),试分别列出y1,y2与x的函数关系式.
问题2:讨论应选择哪家旅行社较优惠.你能想出多少种方法?
解:y1= 80x,
y2= 60x+1000.
解析:根据两家的收费标准,列出函数即可解决问题;
问题1:设学生人数为x,甲、乙两旅行社实际收取总费用为y1,y2(元),试分别列出y1,y2与x的函数关系式.
问题2:讨论应选择哪家旅行社较优惠.你能想出多少种解法?
解法一:从“形”上看
在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
观察图象,可知:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49时,选择甲旅行社费用较少;
当人数为51~100时,选择乙旅行社费用较少.
解法二:从“数”上看
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50.
所以当人数为51~100时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49时,选择甲旅行社费用较少.
解法三:用作差法列出新的方程判断函数值与0的关系.
设选择甲、乙旅行社费用之差为y,则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0) 由图知:
(1)当x=50时,y=0,即y1=y2 ;
(2)当x>50时,y > 0,即y1 > y2 ;
(3)当x<50时,y <0,即y1 < y2 .
活动小结
应用一次函数选择最佳方案
1.从数学的角度分析实际问题,建立函数模型;
2.列出两个一次函数,比较函数值的大小关系;
3.结合实际需求,选择最佳方案.
活动2:小组合作讨论,回答下列问题.
情境:某县区大力发展猕猴桃产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些猕猴桃运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的猕猴桃为x吨,A、B两地运往两仓库的猕猴桃运输费用分别为yA元和yB元.
问题2:试讨论A、B两地中,哪个的运费较少;
问题1:分别求出yA、yB与x之间的函数关系式;
问题3:考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
解:(1)yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
问题1:分别求出yA、yB与x之间的函数关系式;
问题2:试讨论A、B两地中,哪个的运费较少;
(2)因为yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
所以当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少.
问题3:考虑B地的经济承受能力,B地的猕猴桃运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
设两地运费之和为y元,则
y=yA+yB=(-5x+5000)+(3x+4680)=-2x+9680.
由题意得yB=3x+4680≤4830,解得 x≤50.
因为y随x的增大而减小,x最大为50,
所以y最小=-2×50+9680=9580.
在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元.
阅读理解题的解题关键是读懂题意.
第(2)小题比较大小要注意分类讨论,
第(3)小题是利用一次函数的方案设计问题,
一般先根据数量之间的关系建立函数,
然后再利用一次函数的增减性确定出符合要求的最佳方案.
活动小结
1.电信局为满足不同客户的需要,设有A、B两种优惠方案,这两种方案应付话费(元)与通话时间(分钟)之间的关系如图(MN∥CD),若通话时间为500分钟,则应选择哪种方案更优惠( )
A.方案A B.方案B
C.两种方案一样优惠 D.不能确定
B
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程x千米计算,甲汽车租赁公司每月收取的租赁费为y1元,乙汽车租赁公司每月收取的租赁费为y2元.若y1元、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( )
A.当月用车路程为2 000千米时,两家汽车租赁公司
租赁费用相同
B.当月用车路程为2 300千米时,租用乙汽车租赁
公司的车比较合算
C.除去月固定租赁费,甲汽车租赁公司每千米收取的费用比乙汽车租赁公司多
D.甲汽车租赁公司每月的固定租赁费高于乙汽车租赁公司
D
针对本课关键词“方案选择问题”,说说你学到了什么?
利用一次函数进行方案决策
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
