12.1 函数 第2课时 课件(共16张PPT) 沪科版八年级数学上册
文档属性
| 名称 | 12.1 函数 第2课时 课件(共16张PPT) 沪科版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:52:17 | ||
图片预览



文档简介
(共16张PPT)
第十二章 一次函数
12.1 函数
12.1.2 函数的三种表示方法
1.知道表示函数有三种方法,会用列表法、解析法表示函数关系;
2. 掌握函数自变量范围的确定和函数值的求法;
3.能根据实际问题的已知条件,列出简单的函数关系的表达式.
任务一:了解并掌握函数的三种表示方法.
活动:回想上一节课研究的三个问题.
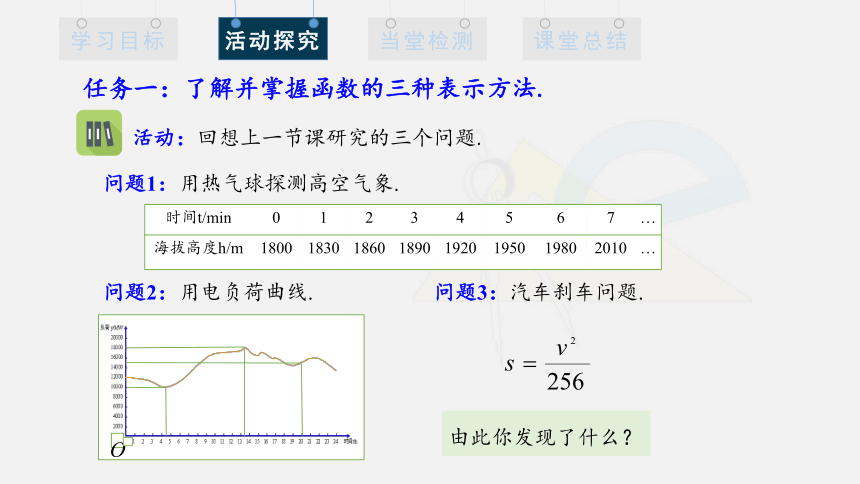
问题1:用热气球探测高空气象.
{10A1B5D5-9B99-4C35-A422-299274C87663}时间t/min
0
1
2
3
4
5
6
7
…
海拔高度h/m
1800
1830
1860
1890
1920
1950
1980
2010
…
问题2:用电负荷曲线.
O
问题3:汽车刹车问题.
由此你发现了什么?
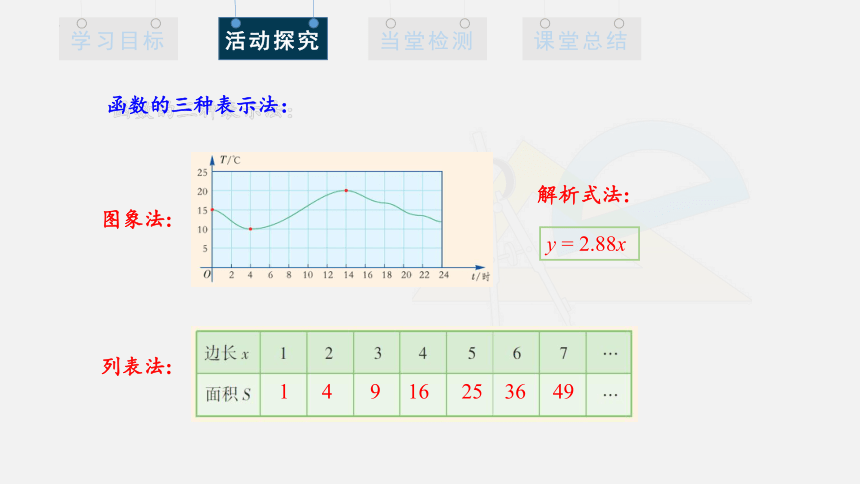
函数的三种表示法:
y = 2.88x
图象法:
列表法:
解析式法:
1 4 9 16 25 36 49
列表法
解析法
图象法
定义
实例
优点
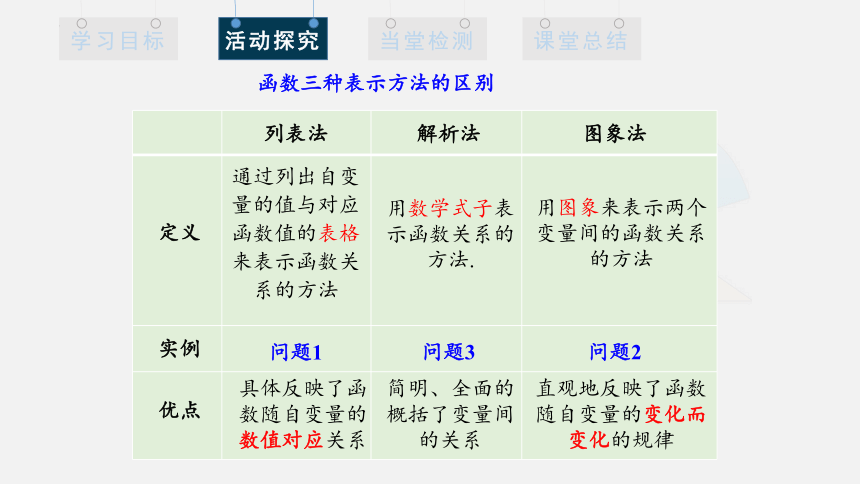
通过列出自变量的值与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法.
问题3
简明、全面的概括了变量间的关系
用图象来表示两个
变量间的函数关系
的方法
问题2
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
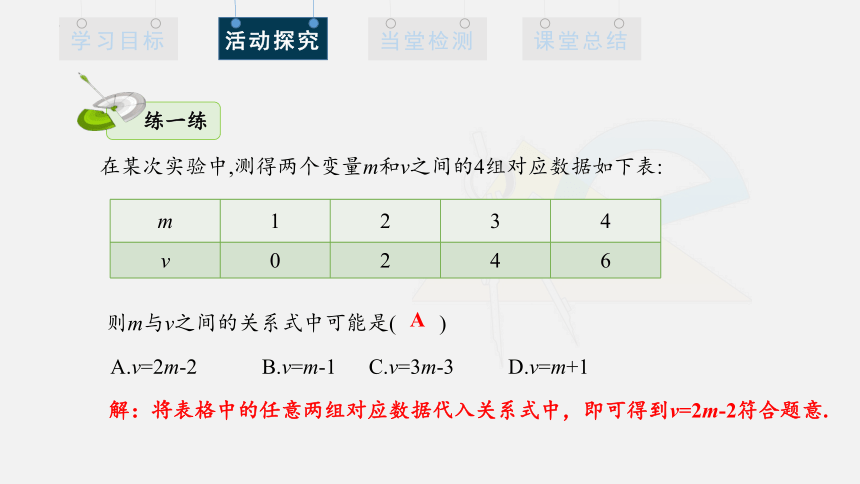
在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
{16D9F66E-5EB9-4882-86FB-DCBF35E3C3E4}m
1
2
3
4
v
0
2
4
6
则m与v之间的关系式中可能是( )
A
A.v=2m-2 B.v=m-1 C.v=3m-3 D.v=m+1
解:将表格中的任意两组对应数据代入关系式中,即可得到v=2m-2符合题意.
练一练
任务二:掌握函数自变量范围的确定和函数值的求法.
活动1:求下列函数中自变量x的取值范围:
(1)y=2x+3; (2)y=-2x2;
(3) (4)
解:(1)x为全体实数; (2)x为全体实数;
(3)x≠2; (4)x≥2.
怎样确定自变量的取值范围呢?
一般主要考虑以下四种情况:
⑴函数表达式为整式形式:自变量取值范围为任意实数;
⑵函数表达式为分式形式:分母≠0;
⑶函数表达式含算术平方根:被开方数≥0;
⑷函数表达式含0指数:底数≠0.
活动小结
函数表达式中自变量的取值范围:
活动2:求函数的自变量x=3时,函数y的值.
(1)y=2x+3; (2)y=-2x2;
(3) (4)
解:当x=3时,(1)y=2x+3=2×3+3=9;
(2)y =-2x2=-2×32=-18;
(3)
(4)
函数 中自变量x的取值范围是 .当x=2时,y= .?
?
x≠1且x≠5
解:函数的表达式是分式时, 需满足分母2x-2≠0且x-5≠0,即x≠1且x≠5,
当x=2时,
遇到这样的综合算式时,不要先化简表达式再求取值范围.
练一练
任务三:能根据实际问题的已知条件,列出简单的函数关系的表达式.
活动:和同伴一起交流,完成下列问题.
问题情境:一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.
问题1:写出游泳池内剩余水量 Q m3与排水时间 t h间的函数表达式;
问题2:写出自变量t的取值范围.
问题3:开始排水 5 h 后,游泳池中还有多少水?
问题4:当游泳池中还剩150 m3水时,已经排水多长时间?
问题1:排水后的剩水量Q m3是排水时间h的函数,有Q=-25 t +300.
问题2:池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t 的取值范围是0≤t≤12.
问题3:当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3
问题4:当Q=150m3时,由150=-25 t +300,得t =6h,即池中还剩水 150 m3 时,已经排水 6 h.
活动小结
(1)自变量自身表示的意义.如时间、耗油量等不能为负数;
(2)问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
在实际问题中确定自变量的取值范围,主要考虑两个因素:
解:根据分式中分母不能为0即可求出x取值范围,由题意得:x-5≠0,解得x≠5.故自变量x的取值范围是x≠5.
解:将x=-1代入得,函数
1.(1)求下列函数 中自变量的取值范围.
(2)当x=-1时,求 的值.
2.暑假里,某校组织部分学生去某地参加数学素质杯夏令营.如果乘车去,汽车行驶的速度为每小时40千米.
{5940675A-B579-460E-94D1-54222C63F5DA}出发后行驶时间t
1小时
2小时
3小时
4小时
5小时
6小时
行驶路程s(千米)
240
200
160
120
80
40
(1)汽车出发后1小时、2小时、3小时……分别行驶了多少千米?请填入下表:
(2)汽车行驶路程 s (千米)与时间 t (小时)的关系式为 .
s=40t
解:结合题意,代入表格中的数据,可得到行驶路程s(千米)与时间t(小时)的关系式s=40t.
函数的
表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
针对本课关键词“函数的三种表示方法”,说说你学到了什么?
第十二章 一次函数
12.1 函数
12.1.2 函数的三种表示方法
1.知道表示函数有三种方法,会用列表法、解析法表示函数关系;
2. 掌握函数自变量范围的确定和函数值的求法;
3.能根据实际问题的已知条件,列出简单的函数关系的表达式.
任务一:了解并掌握函数的三种表示方法.
活动:回想上一节课研究的三个问题.
问题1:用热气球探测高空气象.
{10A1B5D5-9B99-4C35-A422-299274C87663}时间t/min
0
1
2
3
4
5
6
7
…
海拔高度h/m
1800
1830
1860
1890
1920
1950
1980
2010
…
问题2:用电负荷曲线.
O
问题3:汽车刹车问题.
由此你发现了什么?
函数的三种表示法:
y = 2.88x
图象法:
列表法:
解析式法:
1 4 9 16 25 36 49
列表法
解析法
图象法
定义
实例
优点
通过列出自变量的值与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法.
问题3
简明、全面的概括了变量间的关系
用图象来表示两个
变量间的函数关系
的方法
问题2
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法的区别
在某次实验中,测得两个变量m和v之间的4组对应数据如下表:
{16D9F66E-5EB9-4882-86FB-DCBF35E3C3E4}m
1
2
3
4
v
0
2
4
6
则m与v之间的关系式中可能是( )
A
A.v=2m-2 B.v=m-1 C.v=3m-3 D.v=m+1
解:将表格中的任意两组对应数据代入关系式中,即可得到v=2m-2符合题意.
练一练
任务二:掌握函数自变量范围的确定和函数值的求法.
活动1:求下列函数中自变量x的取值范围:
(1)y=2x+3; (2)y=-2x2;
(3) (4)
解:(1)x为全体实数; (2)x为全体实数;
(3)x≠2; (4)x≥2.
怎样确定自变量的取值范围呢?
一般主要考虑以下四种情况:
⑴函数表达式为整式形式:自变量取值范围为任意实数;
⑵函数表达式为分式形式:分母≠0;
⑶函数表达式含算术平方根:被开方数≥0;
⑷函数表达式含0指数:底数≠0.
活动小结
函数表达式中自变量的取值范围:
活动2:求函数的自变量x=3时,函数y的值.
(1)y=2x+3; (2)y=-2x2;
(3) (4)
解:当x=3时,(1)y=2x+3=2×3+3=9;
(2)y =-2x2=-2×32=-18;
(3)
(4)
函数 中自变量x的取值范围是 .当x=2时,y= .?
?
x≠1且x≠5
解:函数的表达式是分式时, 需满足分母2x-2≠0且x-5≠0,即x≠1且x≠5,
当x=2时,
遇到这样的综合算式时,不要先化简表达式再求取值范围.
练一练
任务三:能根据实际问题的已知条件,列出简单的函数关系的表达式.
活动:和同伴一起交流,完成下列问题.
问题情境:一个游泳池内有水300 m3,现打开排水管以每小时25 m3的排出量排水.
问题1:写出游泳池内剩余水量 Q m3与排水时间 t h间的函数表达式;
问题2:写出自变量t的取值范围.
问题3:开始排水 5 h 后,游泳池中还有多少水?
问题4:当游泳池中还剩150 m3水时,已经排水多长时间?
问题1:排水后的剩水量Q m3是排水时间h的函数,有Q=-25 t +300.
问题2:池中共有300 m3水,每小时排水25 m3,故全部排完只需 300÷25=12(h),故自变量 t 的取值范围是0≤t≤12.
问题3:当t=5,代入上式得Q=-5×25+300=175(m3),
即第5h末池中还有水175 m3
问题4:当Q=150m3时,由150=-25 t +300,得t =6h,即池中还剩水 150 m3 时,已经排水 6 h.
活动小结
(1)自变量自身表示的意义.如时间、耗油量等不能为负数;
(2)问题中的限制条件.此时多用不等式或不等式组来确定自变量的取值范围.
在实际问题中确定自变量的取值范围,主要考虑两个因素:
解:根据分式中分母不能为0即可求出x取值范围,由题意得:x-5≠0,解得x≠5.故自变量x的取值范围是x≠5.
解:将x=-1代入得,函数
1.(1)求下列函数 中自变量的取值范围.
(2)当x=-1时,求 的值.
2.暑假里,某校组织部分学生去某地参加数学素质杯夏令营.如果乘车去,汽车行驶的速度为每小时40千米.
{5940675A-B579-460E-94D1-54222C63F5DA}出发后行驶时间t
1小时
2小时
3小时
4小时
5小时
6小时
行驶路程s(千米)
240
200
160
120
80
40
(1)汽车出发后1小时、2小时、3小时……分别行驶了多少千米?请填入下表:
(2)汽车行驶路程 s (千米)与时间 t (小时)的关系式为 .
s=40t
解:结合题意,代入表格中的数据,可得到行驶路程s(千米)与时间t(小时)的关系式s=40t.
函数的
表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
针对本课关键词“函数的三种表示方法”,说说你学到了什么?
