4.5 角的比较与补(余)角 课件 (共18张PPT) 沪科版七年级数学上册
文档属性
| 名称 | 4.5 角的比较与补(余)角 课件 (共18张PPT) 沪科版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:54:57 | ||
图片预览






文档简介
(共18张PPT)
4.5 角的比较与补(余)角
第4章 直线与角
1.会比较角的大小,了解角平分线的概念,进行相关运算;
2.了解余角、补角的概念,掌握其性质.
活动1:有天小明和小红各带了一把折扇(如图),下面是他们的对话:
小明:我的折扇张开大一些,所以我的折扇的角也大一些.
小红:我的折扇长一些,所以我的折扇的角也大一些.
问题:类比线段长度的比较,你们有办法
帮他们进行判断吗
任务一:会比较角的大小,能进行角的运算
小明
小红
小明的折扇角度更大,理由见下一页
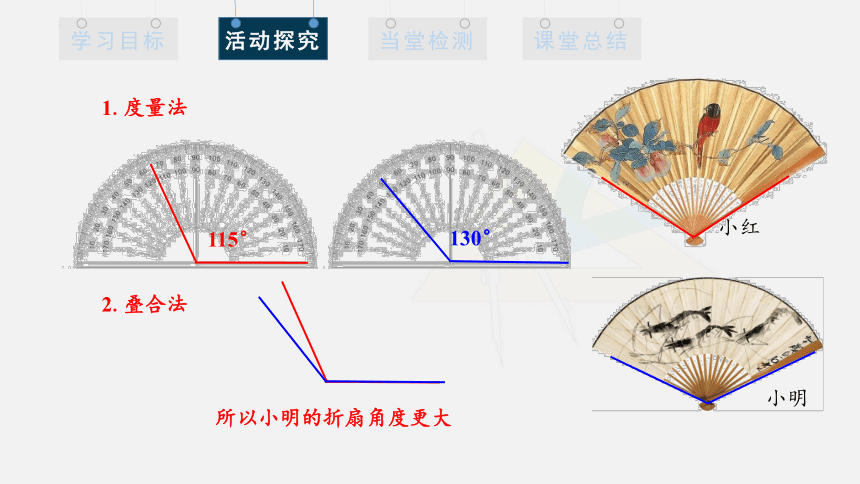
1.度量法
小明
小红
115°
130°
2.叠合法
所以小明的折扇角度更大
1.度量法;
角的大小比较
∠AOB ∠A'O'B'
∠AOB ∠A'O'B'
∠AOB ∠A'O'B'
(O' )
B'
(A' )
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
(O' )
(B' )
(A' )
2.叠合法.
<
=
>
做一做:观察下图,写出图中所有的角及角之间的等量关系.
A
B
O
C
解:3个角,∠AOC,∠AOB,∠COB;
关系是:∠AOC=∠COB+∠BOA或∠AOB=∠AOC-∠COB
或∠COB=∠AOC-∠AOB.
动手操作:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,画出折痕OC,量一量∠AOC和∠BOC的大小,它们有什么关系?
O
B
A
C
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:因为OC是∠AOB的平分线,
所以∠AOC=∠BOC= ∠AOB,
∠AOB=2∠AOC=2∠BOC.
活动2:如图,已知∠AOD=30°,∠BOD是∠AOD的3倍,OC是∠AOB的平分线,求∠AOC和∠COD的度数.
O
A
D
C
B
解:因为∠AOD=30°,∠BOD是∠AOD的3倍,
所以∠BOD=90°,
所以∠AOB=∠BOD+∠AOD=120°,
因为OC是∠AOB的平分线,所以∠AOC= ∠AOB=60°,
所以∠COD=∠AOC-∠AOD=30°.
如图,OC是∠AOB的平分线,OD平分∠AOC,且∠AOB=60°,则∠BOD为 ( )
A. 15° B. 30° C. 45° D. 20°
练一练
C
活动1:如图长方形ABCD,在点A处作一条射线AE交BC边(不含端点)于点E.
任务二:利用余角和补角的概念及性质解决相关问题
解:∠BAE+∠DAE=90°,∠BEA+∠CEA=180°.
A
B
C
D
E
问题:∠BAE与∠DAE有什么数量关系?
∠BEA与∠CEA有什么数量关系?
如果两个角的和等于90°,就说这两个角互为余角(简称为两个角互余).
如果两个角的和等于180°,就说这两个角互为补角(简称为两个角互补).
几何语言:因为∠1+∠2=90°,∠3+∠4=180°,
所以∠1与∠2互余,∠3与∠4互补.
反之:因为∠1与∠2互余,∠3与∠4互补,
所以∠1+∠2=90°,∠3+∠4=180°.
1
2
3
4
互余、互补反映的是数量关系,与位置无关.
活动2:结合已知,回答下列问题.
已知:如图,A,O,B三点在一条直线上,∠AOC=∠DOE=90°.
问题:(1)图中互补的角有哪些?
(2)图中互余的角有哪些?
(3)相等的角有哪些(小于90°的角)?
解:(1)因为A,O,B三点在一条直线上,∠AOC=∠DOE=90°,
所以∠COB+∠AOC=180°,∠AOC+∠DOE=180°,
所以∠COB+∠DOE=180°,
故∠COB与∠AOC,∠AOC与∠DOE,∠COB与∠DOE互补;
(2)由(1)可知:∠COB=180°-∠AOC=90°,即∠3+∠4=90°,
由题可知:∠1+∠2=∠2+∠3=90°,
又∠1+∠4=180°-∠DOE=90°,
故∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4互余;
(3)因为∠1+∠2=∠2+∠3=90°,所以∠1=∠3,同理∠2=∠4.
余角的性质:同角(等角)的余角相等.
补角的性质:同角(等角)的补角相等.
1.若一个角的补角等于它的余角的4倍,求这个角的度数.
练一练
解:设这个角为x°,则它的余角为(90-x)°,补角为(180-x)°,
依题意有:180-x=4(90-x),
解得x=60,
故这个角为60°.
涉及到倍数关系,可借助方程求解.
2.如图,已知∠ACB=∠CDB=90°.
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?
解:(1)因为∠ACB=90°,所以∠1+∠2=90°,∠A+∠B=90°,
又因为∠CDB=90°,所以∠ADC=180°-∠CDB=90°,∠1+∠B=90°,
所以∠A+∠2=90°,
故互余的有:∠1和∠2,∠A和∠B,∠1和∠B,∠A和∠2;
(2)根据同角的余角相等可知:∠A=∠1,∠2=∠B.
A
C
D
1
2
B
1.如图,射线OC,OD分别在∠AOB的内部、外部,下列关系不一定成立的是( )
A.∠AOB<∠AOD
B.∠BOC<∠AOB
C.∠COD<∠AOD
D.∠AOB<∠COD
2.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是______.
D
150°
3.如图OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
O
A
B
C
D
A
回顾本节课,说一说你都学到了哪些知识?
角
角的大小比较
余角和补角
度量法
叠合法
概念
角平分线
性质
4.5 角的比较与补(余)角
第4章 直线与角
1.会比较角的大小,了解角平分线的概念,进行相关运算;
2.了解余角、补角的概念,掌握其性质.
活动1:有天小明和小红各带了一把折扇(如图),下面是他们的对话:
小明:我的折扇张开大一些,所以我的折扇的角也大一些.
小红:我的折扇长一些,所以我的折扇的角也大一些.
问题:类比线段长度的比较,你们有办法
帮他们进行判断吗
任务一:会比较角的大小,能进行角的运算
小明
小红
小明的折扇角度更大,理由见下一页
1.度量法
小明
小红
115°
130°
2.叠合法
所以小明的折扇角度更大
1.度量法;
角的大小比较
∠AOB ∠A'O'B'
∠AOB ∠A'O'B'
∠AOB ∠A'O'B'
(O' )
B'
(A' )
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
(O' )
(B' )
(A' )
2.叠合法.
<
=
>
做一做:观察下图,写出图中所有的角及角之间的等量关系.
A
B
O
C
解:3个角,∠AOC,∠AOB,∠COB;
关系是:∠AOC=∠COB+∠BOA或∠AOB=∠AOC-∠COB
或∠COB=∠AOC-∠AOB.
动手操作:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,画出折痕OC,量一量∠AOC和∠BOC的大小,它们有什么关系?
O
B
A
C
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:因为OC是∠AOB的平分线,
所以∠AOC=∠BOC= ∠AOB,
∠AOB=2∠AOC=2∠BOC.
活动2:如图,已知∠AOD=30°,∠BOD是∠AOD的3倍,OC是∠AOB的平分线,求∠AOC和∠COD的度数.
O
A
D
C
B
解:因为∠AOD=30°,∠BOD是∠AOD的3倍,
所以∠BOD=90°,
所以∠AOB=∠BOD+∠AOD=120°,
因为OC是∠AOB的平分线,所以∠AOC= ∠AOB=60°,
所以∠COD=∠AOC-∠AOD=30°.
如图,OC是∠AOB的平分线,OD平分∠AOC,且∠AOB=60°,则∠BOD为 ( )
A. 15° B. 30° C. 45° D. 20°
练一练
C
活动1:如图长方形ABCD,在点A处作一条射线AE交BC边(不含端点)于点E.
任务二:利用余角和补角的概念及性质解决相关问题
解:∠BAE+∠DAE=90°,∠BEA+∠CEA=180°.
A
B
C
D
E
问题:∠BAE与∠DAE有什么数量关系?
∠BEA与∠CEA有什么数量关系?
如果两个角的和等于90°,就说这两个角互为余角(简称为两个角互余).
如果两个角的和等于180°,就说这两个角互为补角(简称为两个角互补).
几何语言:因为∠1+∠2=90°,∠3+∠4=180°,
所以∠1与∠2互余,∠3与∠4互补.
反之:因为∠1与∠2互余,∠3与∠4互补,
所以∠1+∠2=90°,∠3+∠4=180°.
1
2
3
4
互余、互补反映的是数量关系,与位置无关.
活动2:结合已知,回答下列问题.
已知:如图,A,O,B三点在一条直线上,∠AOC=∠DOE=90°.
问题:(1)图中互补的角有哪些?
(2)图中互余的角有哪些?
(3)相等的角有哪些(小于90°的角)?
解:(1)因为A,O,B三点在一条直线上,∠AOC=∠DOE=90°,
所以∠COB+∠AOC=180°,∠AOC+∠DOE=180°,
所以∠COB+∠DOE=180°,
故∠COB与∠AOC,∠AOC与∠DOE,∠COB与∠DOE互补;
(2)由(1)可知:∠COB=180°-∠AOC=90°,即∠3+∠4=90°,
由题可知:∠1+∠2=∠2+∠3=90°,
又∠1+∠4=180°-∠DOE=90°,
故∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4互余;
(3)因为∠1+∠2=∠2+∠3=90°,所以∠1=∠3,同理∠2=∠4.
余角的性质:同角(等角)的余角相等.
补角的性质:同角(等角)的补角相等.
1.若一个角的补角等于它的余角的4倍,求这个角的度数.
练一练
解:设这个角为x°,则它的余角为(90-x)°,补角为(180-x)°,
依题意有:180-x=4(90-x),
解得x=60,
故这个角为60°.
涉及到倍数关系,可借助方程求解.
2.如图,已知∠ACB=∠CDB=90°.
(1)图中有哪几对互余的角?
(2)图中哪几对角是相等的角(直角除外)?
解:(1)因为∠ACB=90°,所以∠1+∠2=90°,∠A+∠B=90°,
又因为∠CDB=90°,所以∠ADC=180°-∠CDB=90°,∠1+∠B=90°,
所以∠A+∠2=90°,
故互余的有:∠1和∠2,∠A和∠B,∠1和∠B,∠A和∠2;
(2)根据同角的余角相等可知:∠A=∠1,∠2=∠B.
A
C
D
1
2
B
1.如图,射线OC,OD分别在∠AOB的内部、外部,下列关系不一定成立的是( )
A.∠AOB<∠AOD
B.∠BOC<∠AOB
C.∠COD<∠AOD
D.∠AOB<∠COD
2.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是______.
D
150°
3.如图OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
O
A
B
C
D
A
回顾本节课,说一说你都学到了哪些知识?
角
角的大小比较
余角和补角
度量法
叠合法
概念
角平分线
性质
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
