第十九章 一次函数 单元试卷(无答案) 人教版数学八年级下册
文档属性
| 名称 | 第十九章 一次函数 单元试卷(无答案) 人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:52:41 | ||
图片预览


文档简介
2023-2024学年人教版数学八下 第十九章 一次函数 单元试卷
一、选择题
对于一次函数 ,下列结论错误的是
A.若两点 , 在该函数图象上,且 ,则
B.函数的图象不经过第三象限
C.函数的图象向下平移 个单位长度得 的图象
D.函数的图象与 轴的交点坐标是
直线 在坐标系中的位置如图所示,它的函数解析式可能为
A. B.
C. D.
一次函数 的图象过点 ,,,则
A. B. C. D.
如图,直线 和 相交于点 ,则关于 的不等式 的解为
A. B. C. D.
已知等腰三角形的周长为 ,底边长为 ,腰长为 , 与 之间的函数关系式为 ,那么自变量 的取值范围是
A. B. C. D.
一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始 内只进水不出水,从第 分钟到第 分钟内既进水又出水,从第 分钟开始只出水不进水,容器内水量 与时间 之间的函数关系如图所示,则图中 的值是
A. B. C. D.
如图所示,直线 与 的交点的横坐标为 ,则关于 的不等式 的整数解有
A. 个 B. 个 C. 个 D.无数个
某周末,亮亮全家上午 时自驾小汽车从家里出发,到某网红地游玩,该小汽车离家的距离 (千米)与时间 (时)之间的关系如图所示,根据图象提供的有关信息,判断下列说法错误的是
A.景点离亮亮的家 千米 B. 时至 时,小汽车匀速行驶
C.小汽车返程的速度为 千米/时 D.亮亮到家的时间为 时
某公司为调动职工工作积极性,向工会代言人提供了两个加薪方案,要求他从中选择:
方案一: 个月后,在年薪 元的基础上每年提高 元(第一年年薪 元);
方案二: 个月后,在半年薪 元的基础上每半年提高 元(第 个月末发薪水 元).
但不管是选哪一种方案,公司都是每半年发一次工资,如果你是工会代言人,认为哪种方案对员工更有利?
A.方案一
B.方案二
C.两种方案一样
D.工龄短的选方案一,工龄长的选方案二
对于实数 , 我们定义符号 的意义为:当 时,;当 时,.如:.若关于 的函数为 ,则该函数的最小值是
A. B. C. D.
二、填空题
把一次函数 向上平移 个单位,得到函数 .
已知一次函数的图象与直线 在 轴上相交于同一点,且经过点 ,则此一次函数的解析式为 .
已知一次函数 的图象经过第三象限,则 的值为 .
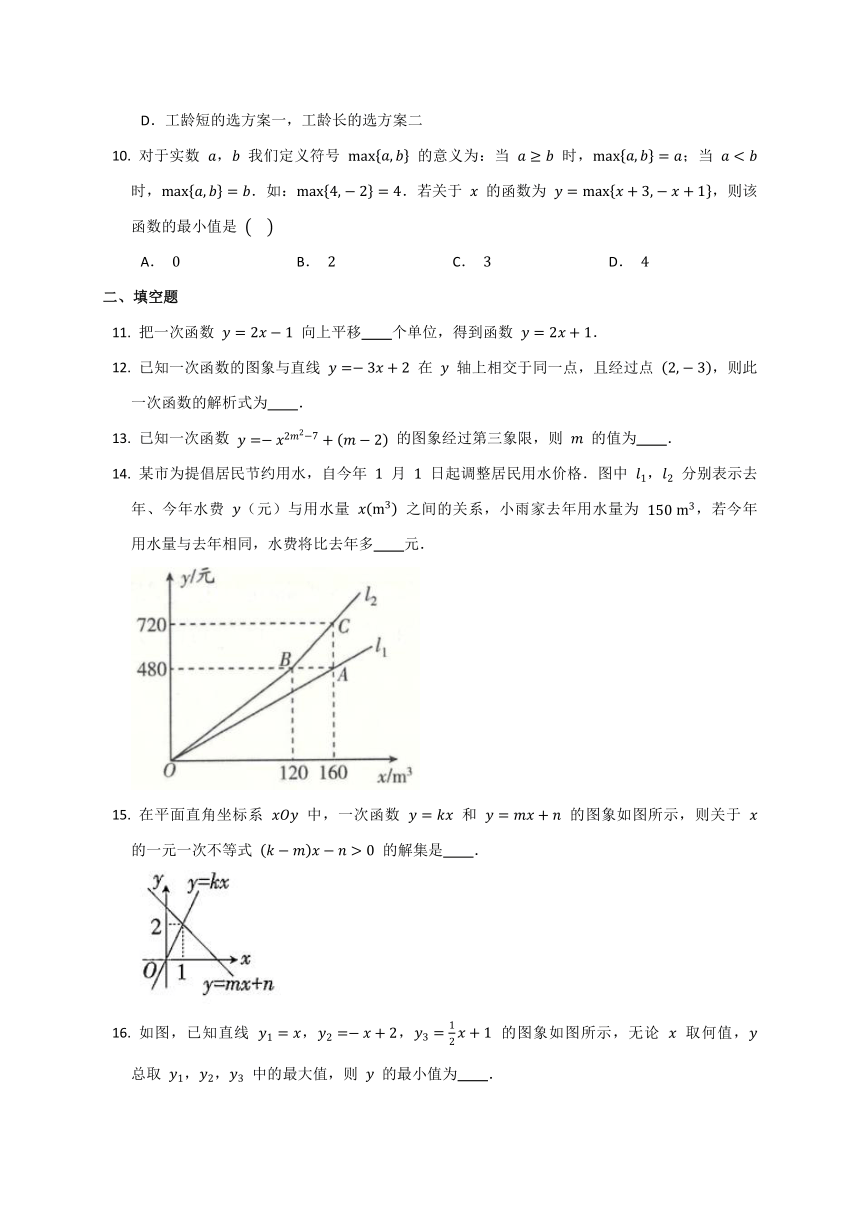
某市为提倡居民节约用水,自今年 月 日起调整居民用水价格.图中 , 分别表示去年、今年水费 (元)与用水量 之间的关系,小雨家去年用水量为 ,若今年用水量与去年相同,水费将比去年多 元.
在平面直角坐标系 中,一次函数 和 的图象如图所示,则关于 的一元一次不等式 的解集是 .
如图,已知直线 ,, 的图象如图所示,无论 取何值, 总取 ,, 中的最大值,则 的最小值为 .
已知过点 的直线与函数 的图象有两个交点,则 的取值范围为 .
一条公路旁依次有 ,, 三个村庄,甲乙两人骑自行车分别从 村、 村同时出发前往 村,甲乙之间的距离 与骑行时间 之间的函数关系如图所示,下列结论:
① , 两村相距 ;
②出发 后两人相遇;
③甲每小时比乙多骑行 ;
④相遇后,乙又骑行了 或 时两人相距 .
其中正确的是 .
三、解答题
已知关于 的一次函数 .
(1) 若这个函数的图象经过原点,求 的值;
(2) 若这个函数的图象不过第四象限,求 的取值范围;
(3) 不论 取何实数,这个函数的图象都过定点,试求这个定点的坐标.
如图,线段 , 分别是一辆轿车的油箱剩余油量 (升)与另一辆客车的油箱剩余油量 (升)关于行驶路程 (千米)的函数图象.
(1) 分别求 , 关于 的函数解析式,并写出定义域;
(2) 如果两车同时出发,轿车的行驶速度为每小时 千米,客车的行驶速度为每小时 千米,当油箱的剩余油量相同时,两车行驶的时间相差几分钟?
小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次 元的包装费外,樱桃不超过 收费 元,超过 ,则超出部分按每千克 元加收费用.设该公司从西安到南昌快递樱桃的费用为 (元),所寄樱桃为 .
(1) 求 与 之间的函数关系式.
(2) 已知小李给外婆快寄了 樱桃,请你求出这次快寄的费用是多少元?
如图,直线 与 轴、 轴分别交于点 ,,与函数 的图象交于点 .
(1) 求 , 的值和不等式 的解集;
(2) 在 轴上有一点 ,过点 作 轴的垂线,分别交函数 和 的图象于点 ,.若 ,求点 的坐标.
某服装店准备购进甲、乙两种服装出售,甲种每件售价120元,乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元,购进3件甲服装的费用和购进4件乙服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲种服装进价为多少元/件?乙种服装进价为多少元/件?
(2)若购进这100件服装的费用不得超过7500元:
① 求甲种服装最多购进多少件?
② 该服装店对甲种服装每件降价元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
甲、乙两车分别从 , 两地同时出发,甲车匀速前往 地,到达 地立即以另一速度按原路匀速返回到 地,乙车匀速前往 地.设甲、乙两车距 地的路程为 ,甲车行驶的时间为 , 与 之间的函数图象如图所示.
(1) 图中, , ;
(2) 求甲车返回时 与 之间的函数关系式,并写出自变量 的取值范围;
(3) 在甲车返回到 地的过程中,当 为何值时,甲、乙两车相距 ?
【阅读理解】
将平面直角坐标系中过某一定点且不与 轴垂直的直线,叫该定点的“奈斯线”,若点 ,则点 的“奈斯线”可记为 .
(1) 【综合运用】
()已知点 的“奈斯线”可记为 ,则点 的坐标为 ;
()若点 的“奈斯线”恰好经过点 ,求该“奈斯线”的解析式.
(2) 【拓展提升】
已知点 在点 的“奈斯线” 上,点 在直线 上,若 ,,且当 时,,请直接确定 的取值范围.
一、选择题
对于一次函数 ,下列结论错误的是
A.若两点 , 在该函数图象上,且 ,则
B.函数的图象不经过第三象限
C.函数的图象向下平移 个单位长度得 的图象
D.函数的图象与 轴的交点坐标是
直线 在坐标系中的位置如图所示,它的函数解析式可能为
A. B.
C. D.
一次函数 的图象过点 ,,,则
A. B. C. D.
如图,直线 和 相交于点 ,则关于 的不等式 的解为
A. B. C. D.
已知等腰三角形的周长为 ,底边长为 ,腰长为 , 与 之间的函数关系式为 ,那么自变量 的取值范围是
A. B. C. D.
一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始 内只进水不出水,从第 分钟到第 分钟内既进水又出水,从第 分钟开始只出水不进水,容器内水量 与时间 之间的函数关系如图所示,则图中 的值是
A. B. C. D.
如图所示,直线 与 的交点的横坐标为 ,则关于 的不等式 的整数解有
A. 个 B. 个 C. 个 D.无数个
某周末,亮亮全家上午 时自驾小汽车从家里出发,到某网红地游玩,该小汽车离家的距离 (千米)与时间 (时)之间的关系如图所示,根据图象提供的有关信息,判断下列说法错误的是
A.景点离亮亮的家 千米 B. 时至 时,小汽车匀速行驶
C.小汽车返程的速度为 千米/时 D.亮亮到家的时间为 时
某公司为调动职工工作积极性,向工会代言人提供了两个加薪方案,要求他从中选择:
方案一: 个月后,在年薪 元的基础上每年提高 元(第一年年薪 元);
方案二: 个月后,在半年薪 元的基础上每半年提高 元(第 个月末发薪水 元).
但不管是选哪一种方案,公司都是每半年发一次工资,如果你是工会代言人,认为哪种方案对员工更有利?
A.方案一
B.方案二
C.两种方案一样
D.工龄短的选方案一,工龄长的选方案二
对于实数 , 我们定义符号 的意义为:当 时,;当 时,.如:.若关于 的函数为 ,则该函数的最小值是
A. B. C. D.
二、填空题
把一次函数 向上平移 个单位,得到函数 .
已知一次函数的图象与直线 在 轴上相交于同一点,且经过点 ,则此一次函数的解析式为 .
已知一次函数 的图象经过第三象限,则 的值为 .
某市为提倡居民节约用水,自今年 月 日起调整居民用水价格.图中 , 分别表示去年、今年水费 (元)与用水量 之间的关系,小雨家去年用水量为 ,若今年用水量与去年相同,水费将比去年多 元.
在平面直角坐标系 中,一次函数 和 的图象如图所示,则关于 的一元一次不等式 的解集是 .
如图,已知直线 ,, 的图象如图所示,无论 取何值, 总取 ,, 中的最大值,则 的最小值为 .
已知过点 的直线与函数 的图象有两个交点,则 的取值范围为 .
一条公路旁依次有 ,, 三个村庄,甲乙两人骑自行车分别从 村、 村同时出发前往 村,甲乙之间的距离 与骑行时间 之间的函数关系如图所示,下列结论:
① , 两村相距 ;
②出发 后两人相遇;
③甲每小时比乙多骑行 ;
④相遇后,乙又骑行了 或 时两人相距 .
其中正确的是 .
三、解答题
已知关于 的一次函数 .
(1) 若这个函数的图象经过原点,求 的值;
(2) 若这个函数的图象不过第四象限,求 的取值范围;
(3) 不论 取何实数,这个函数的图象都过定点,试求这个定点的坐标.
如图,线段 , 分别是一辆轿车的油箱剩余油量 (升)与另一辆客车的油箱剩余油量 (升)关于行驶路程 (千米)的函数图象.
(1) 分别求 , 关于 的函数解析式,并写出定义域;
(2) 如果两车同时出发,轿车的行驶速度为每小时 千米,客车的行驶速度为每小时 千米,当油箱的剩余油量相同时,两车行驶的时间相差几分钟?
小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次 元的包装费外,樱桃不超过 收费 元,超过 ,则超出部分按每千克 元加收费用.设该公司从西安到南昌快递樱桃的费用为 (元),所寄樱桃为 .
(1) 求 与 之间的函数关系式.
(2) 已知小李给外婆快寄了 樱桃,请你求出这次快寄的费用是多少元?
如图,直线 与 轴、 轴分别交于点 ,,与函数 的图象交于点 .
(1) 求 , 的值和不等式 的解集;
(2) 在 轴上有一点 ,过点 作 轴的垂线,分别交函数 和 的图象于点 ,.若 ,求点 的坐标.
某服装店准备购进甲、乙两种服装出售,甲种每件售价120元,乙种每件售价90元.每件甲服装的进价比乙服装的进价贵20元,购进3件甲服装的费用和购进4件乙服装的费用相等,现计划购进两种服装共100件,其中甲种服装不少于65件.
(1)甲种服装进价为多少元/件?乙种服装进价为多少元/件?
(2)若购进这100件服装的费用不得超过7500元:
① 求甲种服装最多购进多少件?
② 该服装店对甲种服装每件降价元,乙种服装价格不变,如果这100件服装都可售完,那么该服装店如何进货才能获得最大利润?
甲、乙两车分别从 , 两地同时出发,甲车匀速前往 地,到达 地立即以另一速度按原路匀速返回到 地,乙车匀速前往 地.设甲、乙两车距 地的路程为 ,甲车行驶的时间为 , 与 之间的函数图象如图所示.
(1) 图中, , ;
(2) 求甲车返回时 与 之间的函数关系式,并写出自变量 的取值范围;
(3) 在甲车返回到 地的过程中,当 为何值时,甲、乙两车相距 ?
【阅读理解】
将平面直角坐标系中过某一定点且不与 轴垂直的直线,叫该定点的“奈斯线”,若点 ,则点 的“奈斯线”可记为 .
(1) 【综合运用】
()已知点 的“奈斯线”可记为 ,则点 的坐标为 ;
()若点 的“奈斯线”恰好经过点 ,求该“奈斯线”的解析式.
(2) 【拓展提升】
已知点 在点 的“奈斯线” 上,点 在直线 上,若 ,,且当 时,,请直接确定 的取值范围.
