鲁教版(五四)八年级上册数学第5章 平行四边形 单元测试卷 (含解析)
文档属性
| 名称 | 鲁教版(五四)八年级上册数学第5章 平行四边形 单元测试卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 287.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 14:59:00 | ||
图片预览

文档简介
鲁教五四新版八年级上学期《第5章 平行四边形》2022年单元测试卷
一.选择题(共5小题)
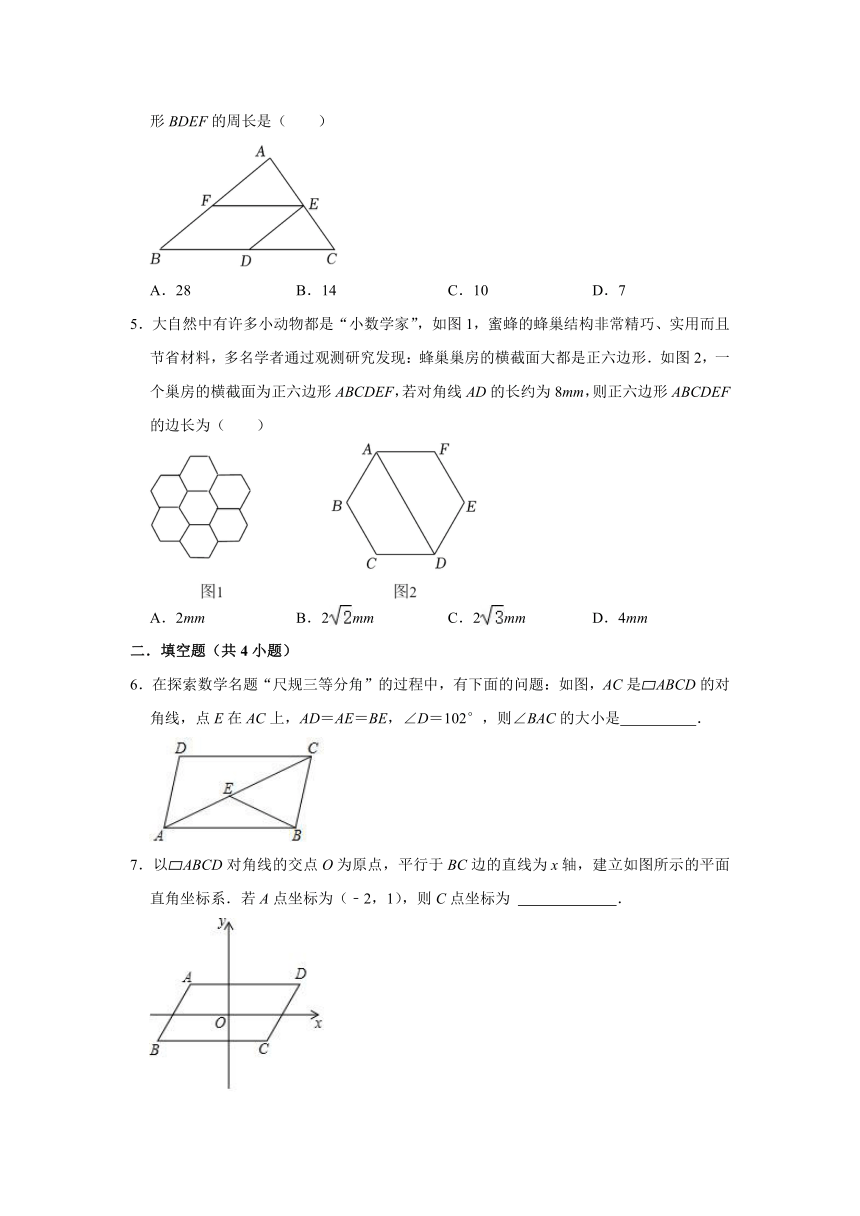
1.如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
A.12 B.15 C.12 D.15
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109° C.110° D.111°
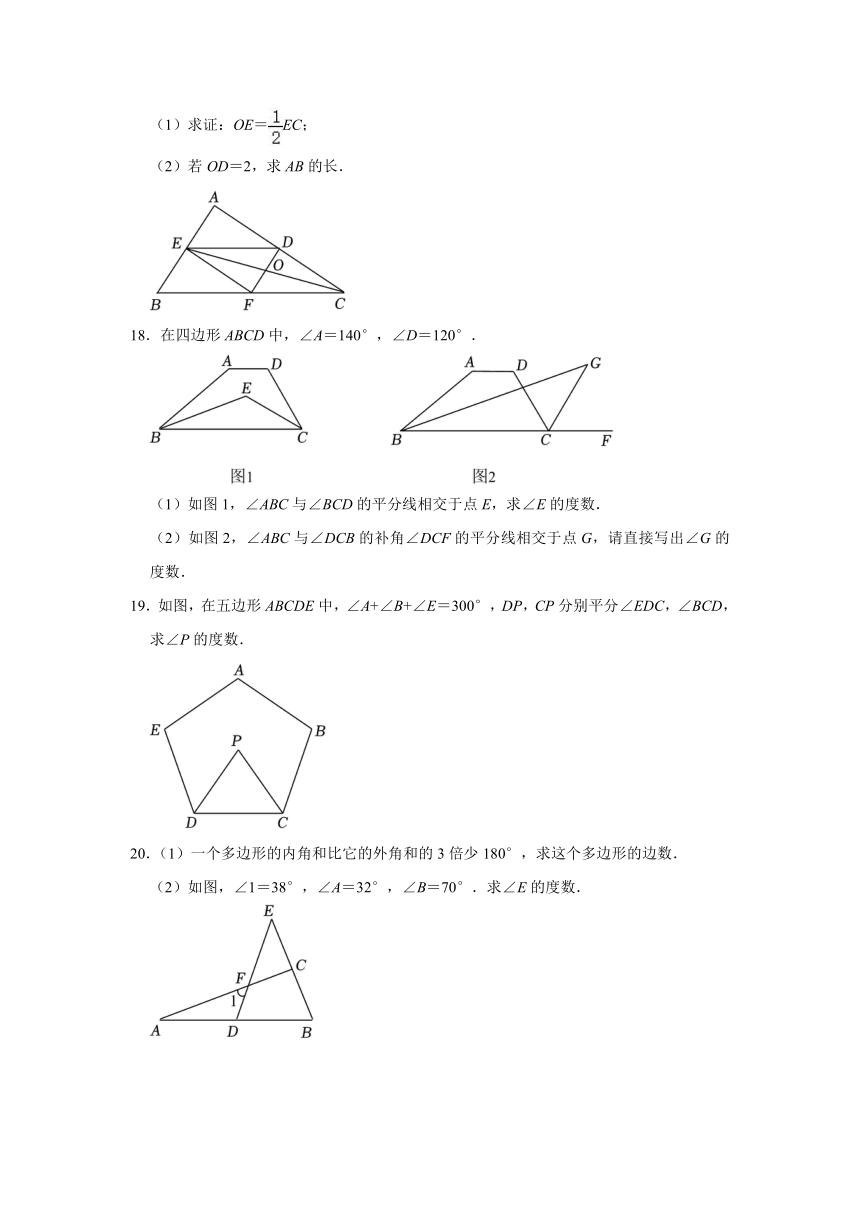
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD周长不变 B.AD=CD
C.四边形ABCD面积不变 D.AD=BC
4.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
5.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为( )
A.2mm B.2mm C.2mm D.4mm
二.填空题(共4小题)
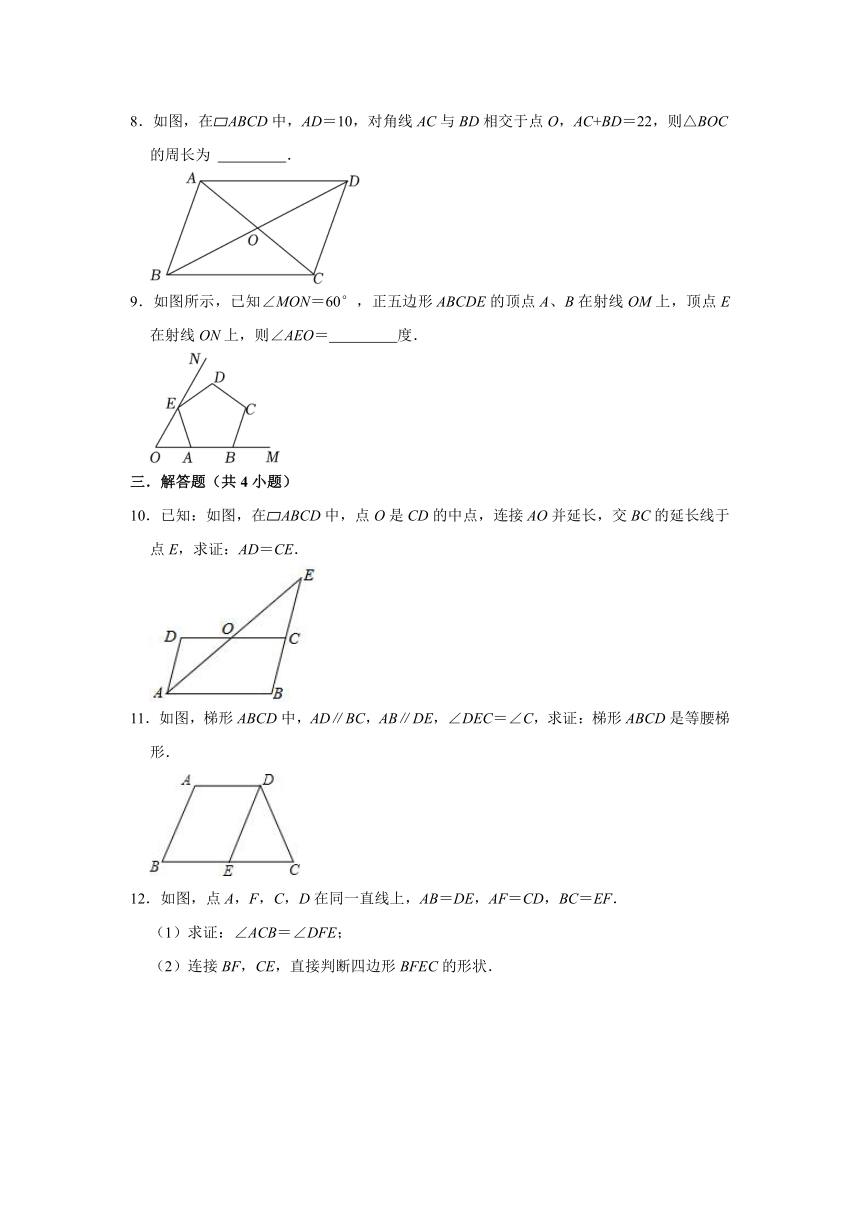
6.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
7.以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为 .
8.如图,在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 .
9.如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO= 度.
三.解答题(共4小题)
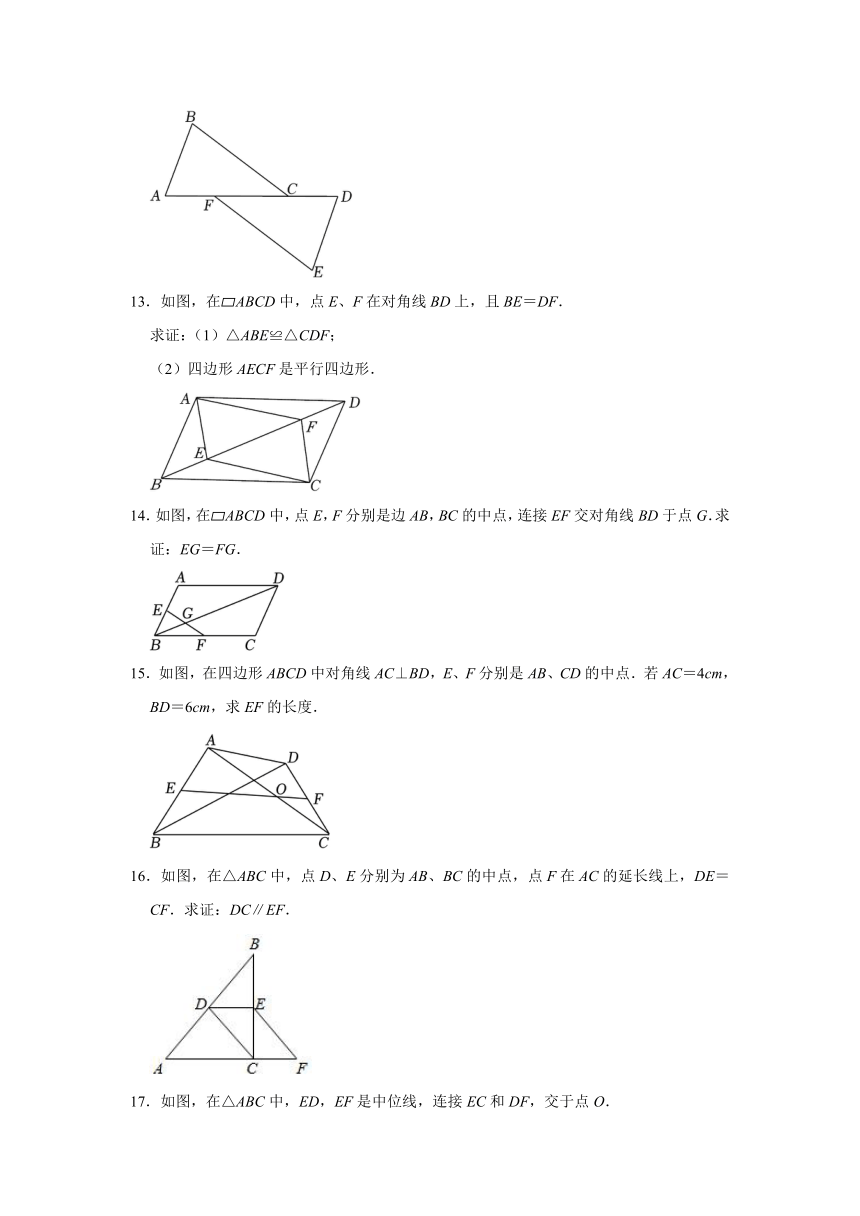
10.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
11.如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
12.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
13.如图,在 ABCD中,点E、F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
14.如图,在 ABCD中,点E,F分别是边AB,BC的中点,连接EF交对角线BD于点G.求证:EG=FG.
15.如图,在四边形ABCD中对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,求EF的长度.
16.如图,在△ABC中,点D、E分别为AB、BC的中点,点F在AC的延长线上,DE=CF.求证:DC∥EF.
17.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OE=EC;
(2)若OD=2,求AB的长.
18.在四边形ABCD中,∠A=140°,∠D=120°.
(1)如图1,∠ABC与∠BCD的平分线相交于点E,求∠E的度数.
(2)如图2,∠ABC与∠DCB的补角∠DCF的平分线相交于点G,请直接写出∠G的度数.
19.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,求∠P的度数.
20.(1)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
(2)如图,∠1=38°,∠A=32°,∠B=70°.求∠E的度数.
6.3-6.4一次函数图像和性质及确定表达式周测试卷
鲁教五四新版八年级上学期《第5章 平行四边形》2022年单元测试卷
参考答案与试题解析
一.选择题(共5小题)
1.如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
A.12 B.15 C.12 D.15
【分析】过点A作AE∥CD,交BC于点E,可得出四边形ADCE是平行四边形,再根据等腰梯形的性质及平行线的性质得出∠AEB=∠BCD=60°,由三角形外角的定义求出∠EAC的度数,故可得出四边形ADCE是菱形,再由等边三角形的判定定理得出△ABE是等边三角形,由此可得出结论.
【解答】解:过点A作AE∥CD,交BC于点E,
∵梯形ABCD是等腰梯形,∠B=60°,
∴AD∥BC,
∴四边形ADCE是平行四边形,
∴∠AEB=∠BCD=60°,
∵CA平分∠BCD,
∴∠ACE=∠BCD=30°,
∵∠AEB是△ACE的外角,
∴∠AEB=∠ACE+∠EAC,即60°=30°+∠EAC,
∴∠EAC=30°,
∴AE=CE=3,
∴四边形ADCE是菱形,
∵△ABE中,∠B=∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=AE=3,
∴梯形ABCD的周长=AB+(BE+CE)+CD+AD=3+3+3+3+3=15.
故选:D.
【点评】本题考查的是等腰梯形的性质,根据题意作出辅助线,构造出平行四边形是解答此题的关键.
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109° C.110° D.111°
【分析】由平行四边形的性质和折叠的性质得∠ABD=∠CDB=∠EBD,再由三角形的外角性质得∠ABD=∠CDB=28°,然后由三角形内角和定理即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
由折叠的性质得:∠EBD=∠ABD,
∴∠ABD=∠CDB=∠EBD,
∵∠1=∠CDB+∠EBD=56°,
∴∠ABD=∠CDB=28°,
∴∠A=180°﹣∠2﹣∠ABD=180°﹣42°﹣28°=110°,
故选:C.
【点评】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理等知识,熟练掌握平行四边形的性质和折叠的性质是解题的关键.
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD周长不变 B.AD=CD
C.四边形ABCD面积不变 D.AD=BC
【分析】由条件可知AB∥CD,AD∥BC,可证明四边形ABCD为平行四边形,可得到AD=BC.
【解答】解:由题意可知:AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AD=BC,
故选:D.
【点评】本题主要考查平行四边形的判定和性质;证明四边形ABCD为平行四边形是解题的关键.
4.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
【分析】根据三角形中位线定理解答即可.
【解答】解:∵D,E,F分别是BC,AC,AB的中点,
∴DE=BF=AB=3,
∵E、F分别为AC、AB中点,
∴EF=BD=BC=4,
∴四边形BDEF的周长为:2×(3+4)=14,
故选:B.
【点评】本题考查了三角形的中位线定理,熟练掌握三角形中位线定理是解题的关键.
5.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为( )
A.2mm B.2mm C.2mm D.4mm
【分析】根据正六边形的性质和题目中的数据,可以求得正六边形ABCDEF的边长.
【解答】解:连接BE,CF,BE、CF交于点O,如图所示,
∵六边形ABCDEF是正六边形,AD的长约为8mm,
∴∠AOF=60°,OA=OD=OF,OA和OD约为4mm,
∴AF约为4mm,
故选:D.
【点评】本题考查多边形的对角线,解答本题的关键是明确正六边形的特点.
二.填空题(共4小题)
6.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 26° .
【分析】根据平行四边形的性质得到∠ABC=∠D=102°,AD=BC,根据等腰三角形的性质得到∠EAB=∠EBA,∠BEC=∠ECB,根据三角形外角的性质得到∠ACB=2∠CAB,由三角形的内角和定理即可得到结论.
【解答】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
故答案为:26°.
【点评】本题考查了平行四边形的性质,三角形的内角和定理,三角形外角的性质,正确的识别图形是解题的关键.
7.以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为 (2,﹣1) .
【分析】根据平行四边形是中心对称图形,再根据 ABCD对角线的交点O为原点和点A的坐标,即可得到点C的坐标.
【解答】解:方法一:∵ ABCD对角线的交点O为原点,
∴ ABCD的A点和C点关于点O中心对称,
∵A点坐标为(﹣2,1),
∴点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
方法二:∵四边形ABCD为平行四边形,
∴点A和C关于对角线的交点O对称,
又∵O为原点,
∴点A和C关于原点对称,
∵点A(﹣2,1),
∴点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
【点评】本题考查平行四边形的性质、坐标与图形性质,解答本题的关键是明确题意,利用平行四边形的性质解答.
8.如图,在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 21 .
【分析】根据平行四边形对角线互相平分,求出OC+OB的长,即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴AO=OC=AC,BO=OD=BD,AD=BC=10,
∵AC+BD=22,
∴OC+BO=11,
∴△BOC的周长=OC+OB+BC=11+10=21.
故答案为:21.
【点评】本题考查平行四边形的性质以及三角形周长等知识,解题的关键是记住平行四边形的对角线互相平分,属于中考基础题.
9.如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO= 48 度.
【分析】根据正五边形的性质求出∠EAB,根据三角形的外角性质计算,得到答案.
【解答】解:∵五边形ABCDE是正五边形,
∴∠EAB==108°,
∵∠EAB是△AEO的外角,
∴∠AEO=∠EAB﹣∠MON=108°﹣60°=48°,
故答案为:48.
【点评】本题考查的是正多边形,掌握多边形内角和定理、正多边形的性质、三角形的外角性质是解题的关键.
三.解答题(共4小题)
10.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
【分析】只要证明△AOD≌△EOC(ASA)即可解决问题;
【解答】证明:∵O是CD的中点,
∴OD=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA),
∴AD=CE.
【点评】此题主要考查了全等三角形的判定与性质,平行四边形的性质等知识,解题的关键是正确寻找全等三角形解决问题.
11.如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
【分析】由AB∥DE,∠DEC=∠C,易证得∠B=∠C,又由同一底上两个角相等的梯形是等腰梯形,即可证得结论.
【解答】证明:∵AB∥DE,
∴∠DEC=∠B,
∵∠DEC=∠C,
∴∠B=∠C,
∴梯形ABCD是等腰梯形.
【点评】此题考查了等腰梯形的判定.此题比较简单,注意掌握同一底上两个角相等的梯形是等腰梯形定理的应用,注意数形结合思想的应用.
12.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
【分析】(1)证△ABC≌△DEF(SSS),再由全等三角形的性质即可得出结论;
(2)由(1)可知,∠ACB=∠DFE,则BC∥EF,再由平行四边形的判定即可得出结论.
【解答】(1)证明:∵AF=CD,
∴AF+CF=CD+CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE;
(2)解:如图,四边形BFEC是平行四边形,理由如下:
由(1)可知,∠ACB=∠DFE,
∴BC∥EF,
又∵BC=EF,
∴四边形BFEC是平行四边形.
【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定等知识,熟练掌握平行四边形的判定方法,证明三角形全等是解题的关键.
13.如图,在 ABCD中,点E、F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【分析】(1)根据平行四边形的性质得到AB=CD,AB∥CD,根据平行线的性质得到∠ABD=∠CDB,利用SAS定理证明△ABE≌△CDF;
(2)根据全等三角形的性质得到AE=CF,∠AEB=∠CFD,根据平行线的判定定理证明AE∥CF,再根据平行四边形的判定定理证明结论.
【解答】证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°﹣∠AEB=180°﹣∠CFD,即∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
【点评】本题考查的是平行四边形的判定和性质、全等三角形的判定和性质,掌握平行四边形的对边平行且相等、一组对边平行且相等的四边形是平行四边形是解题的关键.
声
14.如图,在 ABCD中,点E,F分别是边AB,BC的中点,连接EF交对角线BD于点G.求证:EG=FG.
【分析】利用三角形中位线定理以及平行四边形的判定定理得到四边形OEBF是平行四边形,据此即可得到EG=FG.
【解答】证明:连接AC,交BD于点O,
连接OE,OF,
∵四边形ABCD平行是平行四边形,
∴OA=OC,
∵点E,F分别是边AB,BC的中点,
∴AE=BE,BF=CF,
∴OE∥BC,OF∥AB,
∴四边形OEBF是平行四边形,
∴EG=GF.
【点评】本题考查了三角形中位线定理,平行四边形的判定和性质,解题的关键是灵活运用所学知识解决问题.
15.如图,在四边形ABCD中对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,求EF的长度.
【分析】取BC的中点H,连接EH、FH,根据三角形中位线定理求出EH、FH,根据勾股定理计算即可.
【解答】解:取BC的中点H,连接EH、FH,如图所示:
∵E、F分别是AB、CD的中点,
∴EH是△ABC的中位线,FH是△BCD的中位线,
∴,,EH∥AC,FH∥BD,
∴∠EHF=90°,
∴.
【点评】本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
16.如图,在△ABC中,点D、E分别为AB、BC的中点,点F在AC的延长线上,DE=CF.求证:DC∥EF.
【分析】根据三角形中位线定理得到DE∥AC,进而证明四边形CDEF为平行四边形,根据平行四边形的性质证明即可.
【解答】证明:∵点D、E分别为AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
∵DE=CF,
∴四边形CDEF为平行四边形,
∴DC∥EF.
【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
17.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OE=EC;
(2)若OD=2,求AB的长.
【分析】(1)证明四边形EFCD是平行四边形即可得出结论;
(2)证明DF是△ABC的中位线即可求解.
【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE=;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF=,
∴AB=2DF=8.
【点评】本题考查了三角形中位线定理,熟练掌握三角形中位线定理是解题的关键.
18.在四边形ABCD中,∠A=140°,∠D=120°.
(1)如图1,∠ABC与∠BCD的平分线相交于点E,求∠E的度数.
(2)如图2,∠ABC与∠DCB的补角∠DCF的平分线相交于点G,请直接写出∠G的度数.
【分析】(1)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数;
(2)根据四边形的内角和定理表示出∠BCD,再表示出∠DCF,然后根据角平分线的定义可得∠GBC=∠ABC,∠GCF=∠DCF,三角形的一个外角等于与它不相邻的两个内角的和可得∠G+∠GBC=∠GCF,然后整理即可得解
【解答】解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠D=360°﹣140°﹣120°=100°.
∵∠EBC=∠ABC,∠BCE=∠BCD,
∴∠E=180﹣∠EBC﹣∠BCE=180°﹣(∠ABC+∠BCD)=180°﹣×100°=130°.
(2)由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCF=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得∠GCE=∠G+∠GBC,
∵BG、CG分别是∠ABC和∠DCF的平分线,如图2中,
∴∠PBC=∠ABC,∠PCF=∠DCF,
∴∠G+∠GBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠G=(∠A+∠D)﹣90°,
∵∠A=140°,∠D=120°,
∴∠G=(∠A+∠D)﹣90°=40°.
【点评】本题解决的关键是综合运用四边形的内角和以及三角形的内角和、熟练运用平行线的性质和角平分线的定义.
19.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,求∠P的度数.
【分析】根据五边形的内角和求出∠BCD和∠CDE的和,再根据角平分线及三角形内角和求出∠P的度数.
【解答】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=240°;
∵DP,CP分别平分∠EDC,∠BCD,
∴,
∴∠P=180°﹣(∠PCD+∠CDP)=180°﹣120°=60°;
故答案为:60°.
【点评】本题主要考查了多边形的内角和公式、角平分线的定义等知识点,熟记公式以及整体思想的运用是解答本题的关键.
20.(1)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
(2)如图,∠1=38°,∠A=32°,∠B=70°.求∠E的度数.
【分析】(1)多边形的外角和是360度,根据多边形的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数.
(2)先根据三角形外角的性质求出∠EDB的度数,再由三角形内角和定理求出∠E的度数即可.
【解答】解:(1)设这个多边形的边数是n,
依题意得(n﹣2)×180°=3×360°﹣180°,
(n﹣2)=6﹣1,
n=7.
∴这个多边形的边数是7.
(2)∵∠EDB是△ADF的外角,∠1=38°,∠A=32°,
∴∠EDB=∠A+∠1=32°+38°=70°,
∵△EDB中,∠EDB=70°,∠B=70°,
∴∠E=180°﹣(∠B+∠EDB)=180°﹣(70°+70°)=40°.
【点评】本题考查的是三角形外角的性质,即三角形的一个外角等于和它不相邻的两个内角的和.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/12/15 16:27:30;用户:陈振君;邮箱:18253
一.选择题(共5小题)
1.如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
A.12 B.15 C.12 D.15
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109° C.110° D.111°
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD周长不变 B.AD=CD
C.四边形ABCD面积不变 D.AD=BC
4.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
5.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为( )
A.2mm B.2mm C.2mm D.4mm
二.填空题(共4小题)
6.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 .
7.以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为 .
8.如图,在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 .
9.如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO= 度.
三.解答题(共4小题)
10.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
11.如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
12.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
13.如图,在 ABCD中,点E、F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
14.如图,在 ABCD中,点E,F分别是边AB,BC的中点,连接EF交对角线BD于点G.求证:EG=FG.
15.如图,在四边形ABCD中对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,求EF的长度.
16.如图,在△ABC中,点D、E分别为AB、BC的中点,点F在AC的延长线上,DE=CF.求证:DC∥EF.
17.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OE=EC;
(2)若OD=2,求AB的长.
18.在四边形ABCD中,∠A=140°,∠D=120°.
(1)如图1,∠ABC与∠BCD的平分线相交于点E,求∠E的度数.
(2)如图2,∠ABC与∠DCB的补角∠DCF的平分线相交于点G,请直接写出∠G的度数.
19.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,求∠P的度数.
20.(1)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
(2)如图,∠1=38°,∠A=32°,∠B=70°.求∠E的度数.
6.3-6.4一次函数图像和性质及确定表达式周测试卷
鲁教五四新版八年级上学期《第5章 平行四边形》2022年单元测试卷
参考答案与试题解析
一.选择题(共5小题)
1.如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
A.12 B.15 C.12 D.15
【分析】过点A作AE∥CD,交BC于点E,可得出四边形ADCE是平行四边形,再根据等腰梯形的性质及平行线的性质得出∠AEB=∠BCD=60°,由三角形外角的定义求出∠EAC的度数,故可得出四边形ADCE是菱形,再由等边三角形的判定定理得出△ABE是等边三角形,由此可得出结论.
【解答】解:过点A作AE∥CD,交BC于点E,
∵梯形ABCD是等腰梯形,∠B=60°,
∴AD∥BC,
∴四边形ADCE是平行四边形,
∴∠AEB=∠BCD=60°,
∵CA平分∠BCD,
∴∠ACE=∠BCD=30°,
∵∠AEB是△ACE的外角,
∴∠AEB=∠ACE+∠EAC,即60°=30°+∠EAC,
∴∠EAC=30°,
∴AE=CE=3,
∴四边形ADCE是菱形,
∵△ABE中,∠B=∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=AE=3,
∴梯形ABCD的周长=AB+(BE+CE)+CD+AD=3+3+3+3+3=15.
故选:D.
【点评】本题考查的是等腰梯形的性质,根据题意作出辅助线,构造出平行四边形是解答此题的关键.
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°,则∠A的度数为( )
A.108° B.109° C.110° D.111°
【分析】由平行四边形的性质和折叠的性质得∠ABD=∠CDB=∠EBD,再由三角形的外角性质得∠ABD=∠CDB=28°,然后由三角形内角和定理即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
由折叠的性质得:∠EBD=∠ABD,
∴∠ABD=∠CDB=∠EBD,
∵∠1=∠CDB+∠EBD=56°,
∴∠ABD=∠CDB=28°,
∴∠A=180°﹣∠2﹣∠ABD=180°﹣42°﹣28°=110°,
故选:C.
【点评】本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理等知识,熟练掌握平行四边形的性质和折叠的性质是解题的关键.
3.如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形ABCD周长不变 B.AD=CD
C.四边形ABCD面积不变 D.AD=BC
【分析】由条件可知AB∥CD,AD∥BC,可证明四边形ABCD为平行四边形,可得到AD=BC.
【解答】解:由题意可知:AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AD=BC,
故选:D.
【点评】本题主要考查平行四边形的判定和性质;证明四边形ABCD为平行四边形是解题的关键.
4.如图,在△ABC中,D,E,F分别是BC,AC,AB的中点.若AB=6,BC=8,则四边形BDEF的周长是( )
A.28 B.14 C.10 D.7
【分析】根据三角形中位线定理解答即可.
【解答】解:∵D,E,F分别是BC,AC,AB的中点,
∴DE=BF=AB=3,
∵E、F分别为AC、AB中点,
∴EF=BD=BC=4,
∴四边形BDEF的周长为:2×(3+4)=14,
故选:B.
【点评】本题考查了三角形的中位线定理,熟练掌握三角形中位线定理是解题的关键.
5.大自然中有许多小动物都是“小数学家”,如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形.如图2,一个巢房的横截面为正六边形ABCDEF,若对角线AD的长约为8mm,则正六边形ABCDEF的边长为( )
A.2mm B.2mm C.2mm D.4mm
【分析】根据正六边形的性质和题目中的数据,可以求得正六边形ABCDEF的边长.
【解答】解:连接BE,CF,BE、CF交于点O,如图所示,
∵六边形ABCDEF是正六边形,AD的长约为8mm,
∴∠AOF=60°,OA=OD=OF,OA和OD约为4mm,
∴AF约为4mm,
故选:D.
【点评】本题考查多边形的对角线,解答本题的关键是明确正六边形的特点.
二.填空题(共4小题)
6.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC是 ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的大小是 26° .
【分析】根据平行四边形的性质得到∠ABC=∠D=102°,AD=BC,根据等腰三角形的性质得到∠EAB=∠EBA,∠BEC=∠ECB,根据三角形外角的性质得到∠ACB=2∠CAB,由三角形的内角和定理即可得到结论.
【解答】解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
故答案为:26°.
【点评】本题考查了平行四边形的性质,三角形的内角和定理,三角形外角的性质,正确的识别图形是解题的关键.
7.以 ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角坐标系.若A点坐标为(﹣2,1),则C点坐标为 (2,﹣1) .
【分析】根据平行四边形是中心对称图形,再根据 ABCD对角线的交点O为原点和点A的坐标,即可得到点C的坐标.
【解答】解:方法一:∵ ABCD对角线的交点O为原点,
∴ ABCD的A点和C点关于点O中心对称,
∵A点坐标为(﹣2,1),
∴点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
方法二:∵四边形ABCD为平行四边形,
∴点A和C关于对角线的交点O对称,
又∵O为原点,
∴点A和C关于原点对称,
∵点A(﹣2,1),
∴点C的坐标为(2,﹣1),
故答案为:(2,﹣1).
【点评】本题考查平行四边形的性质、坐标与图形性质,解答本题的关键是明确题意,利用平行四边形的性质解答.
8.如图,在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 21 .
【分析】根据平行四边形对角线互相平分,求出OC+OB的长,即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴AO=OC=AC,BO=OD=BD,AD=BC=10,
∵AC+BD=22,
∴OC+BO=11,
∴△BOC的周长=OC+OB+BC=11+10=21.
故答案为:21.
【点评】本题考查平行四边形的性质以及三角形周长等知识,解题的关键是记住平行四边形的对角线互相平分,属于中考基础题.
9.如图所示,已知∠MON=60°,正五边形ABCDE的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO= 48 度.
【分析】根据正五边形的性质求出∠EAB,根据三角形的外角性质计算,得到答案.
【解答】解:∵五边形ABCDE是正五边形,
∴∠EAB==108°,
∵∠EAB是△AEO的外角,
∴∠AEO=∠EAB﹣∠MON=108°﹣60°=48°,
故答案为:48.
【点评】本题考查的是正多边形,掌握多边形内角和定理、正多边形的性质、三角形的外角性质是解题的关键.
三.解答题(共4小题)
10.已知:如图,在 ABCD中,点O是CD的中点,连接AO并延长,交BC的延长线于点E,求证:AD=CE.
【分析】只要证明△AOD≌△EOC(ASA)即可解决问题;
【解答】证明:∵O是CD的中点,
∴OD=CO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠D=∠OCE,
在△ADO和△ECO中,
,
∴△AOD≌△EOC(ASA),
∴AD=CE.
【点评】此题主要考查了全等三角形的判定与性质,平行四边形的性质等知识,解题的关键是正确寻找全等三角形解决问题.
11.如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
【分析】由AB∥DE,∠DEC=∠C,易证得∠B=∠C,又由同一底上两个角相等的梯形是等腰梯形,即可证得结论.
【解答】证明:∵AB∥DE,
∴∠DEC=∠B,
∵∠DEC=∠C,
∴∠B=∠C,
∴梯形ABCD是等腰梯形.
【点评】此题考查了等腰梯形的判定.此题比较简单,注意掌握同一底上两个角相等的梯形是等腰梯形定理的应用,注意数形结合思想的应用.
12.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
【分析】(1)证△ABC≌△DEF(SSS),再由全等三角形的性质即可得出结论;
(2)由(1)可知,∠ACB=∠DFE,则BC∥EF,再由平行四边形的判定即可得出结论.
【解答】(1)证明:∵AF=CD,
∴AF+CF=CD+CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE;
(2)解:如图,四边形BFEC是平行四边形,理由如下:
由(1)可知,∠ACB=∠DFE,
∴BC∥EF,
又∵BC=EF,
∴四边形BFEC是平行四边形.
【点评】本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定等知识,熟练掌握平行四边形的判定方法,证明三角形全等是解题的关键.
13.如图,在 ABCD中,点E、F在对角线BD上,且BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【分析】(1)根据平行四边形的性质得到AB=CD,AB∥CD,根据平行线的性质得到∠ABD=∠CDB,利用SAS定理证明△ABE≌△CDF;
(2)根据全等三角形的性质得到AE=CF,∠AEB=∠CFD,根据平行线的判定定理证明AE∥CF,再根据平行四边形的判定定理证明结论.
【解答】证明:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)由(1)可知,△ABE≌△CDF,
∴AE=CF,∠AEB=∠CFD,
∴180°﹣∠AEB=180°﹣∠CFD,即∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
【点评】本题考查的是平行四边形的判定和性质、全等三角形的判定和性质,掌握平行四边形的对边平行且相等、一组对边平行且相等的四边形是平行四边形是解题的关键.
声
14.如图,在 ABCD中,点E,F分别是边AB,BC的中点,连接EF交对角线BD于点G.求证:EG=FG.
【分析】利用三角形中位线定理以及平行四边形的判定定理得到四边形OEBF是平行四边形,据此即可得到EG=FG.
【解答】证明:连接AC,交BD于点O,
连接OE,OF,
∵四边形ABCD平行是平行四边形,
∴OA=OC,
∵点E,F分别是边AB,BC的中点,
∴AE=BE,BF=CF,
∴OE∥BC,OF∥AB,
∴四边形OEBF是平行四边形,
∴EG=GF.
【点评】本题考查了三角形中位线定理,平行四边形的判定和性质,解题的关键是灵活运用所学知识解决问题.
15.如图,在四边形ABCD中对角线AC⊥BD,E、F分别是AB、CD的中点.若AC=4cm,BD=6cm,求EF的长度.
【分析】取BC的中点H,连接EH、FH,根据三角形中位线定理求出EH、FH,根据勾股定理计算即可.
【解答】解:取BC的中点H,连接EH、FH,如图所示:
∵E、F分别是AB、CD的中点,
∴EH是△ABC的中位线,FH是△BCD的中位线,
∴,,EH∥AC,FH∥BD,
∴∠EHF=90°,
∴.
【点评】本题考查的是三角形中位线定理的应用,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.
16.如图,在△ABC中,点D、E分别为AB、BC的中点,点F在AC的延长线上,DE=CF.求证:DC∥EF.
【分析】根据三角形中位线定理得到DE∥AC,进而证明四边形CDEF为平行四边形,根据平行四边形的性质证明即可.
【解答】证明:∵点D、E分别为AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
∵DE=CF,
∴四边形CDEF为平行四边形,
∴DC∥EF.
【点评】本题考查的是三角形中位线定理、平行四边形的判定和性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.
17.如图,在△ABC中,ED,EF是中位线,连接EC和DF,交于点O.
(1)求证:OE=EC;
(2)若OD=2,求AB的长.
【分析】(1)证明四边形EFCD是平行四边形即可得出结论;
(2)证明DF是△ABC的中位线即可求解.
【解答】(1)证明:∵ED,EF是中位线,
∴ED∥FC,EF∥DC,
∴四边形EFCD是平行四边形,
∵对角线CE和DF相交于点O,
∴OE=;
(2)解:∵EC,DF是平行四边形EFCD的对角线,OD=2,
∴DF=2OD=4,
∵ED,EF是△ABC的中位线,
∴点D,F分别是AC,BC的中点,
∴DF是△ABC的中位线,
∴DF=,
∴AB=2DF=8.
【点评】本题考查了三角形中位线定理,熟练掌握三角形中位线定理是解题的关键.
18.在四边形ABCD中,∠A=140°,∠D=120°.
(1)如图1,∠ABC与∠BCD的平分线相交于点E,求∠E的度数.
(2)如图2,∠ABC与∠DCB的补角∠DCF的平分线相交于点G,请直接写出∠G的度数.
【分析】(1)根据四边形的内角和定理以及角平分线的概念求得∠EBC+∠ECB的度数,再进一步求得∠BEC的度数;
(2)根据四边形的内角和定理表示出∠BCD,再表示出∠DCF,然后根据角平分线的定义可得∠GBC=∠ABC,∠GCF=∠DCF,三角形的一个外角等于与它不相邻的两个内角的和可得∠G+∠GBC=∠GCF,然后整理即可得解
【解答】解:∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°﹣∠A﹣∠D=360°﹣140°﹣120°=100°.
∵∠EBC=∠ABC,∠BCE=∠BCD,
∴∠E=180﹣∠EBC﹣∠BCE=180°﹣(∠ABC+∠BCD)=180°﹣×100°=130°.
(2)由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,
∴∠DCF=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,
由三角形的外角性质得∠GCE=∠G+∠GBC,
∵BG、CG分别是∠ABC和∠DCF的平分线,如图2中,
∴∠PBC=∠ABC,∠PCF=∠DCF,
∴∠G+∠GBC=(∠A+∠D+∠ABC﹣180°)=(∠A+∠D)+∠ABC﹣90°,
∴∠G=(∠A+∠D)﹣90°,
∵∠A=140°,∠D=120°,
∴∠G=(∠A+∠D)﹣90°=40°.
【点评】本题解决的关键是综合运用四边形的内角和以及三角形的内角和、熟练运用平行线的性质和角平分线的定义.
19.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,求∠P的度数.
【分析】根据五边形的内角和求出∠BCD和∠CDE的和,再根据角平分线及三角形内角和求出∠P的度数.
【解答】解:∵五边形的内角和等于540°,∠A+∠B+∠E=300°,
∴∠BCD+∠CDE=240°;
∵DP,CP分别平分∠EDC,∠BCD,
∴,
∴∠P=180°﹣(∠PCD+∠CDP)=180°﹣120°=60°;
故答案为:60°.
【点评】本题主要考查了多边形的内角和公式、角平分线的定义等知识点,熟记公式以及整体思想的运用是解答本题的关键.
20.(1)一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数.
(2)如图,∠1=38°,∠A=32°,∠B=70°.求∠E的度数.
【分析】(1)多边形的外角和是360度,根据多边形的内角和比它的外角和的3倍少180°,即可得到多边形的内角和的度数.根据多边形的内角和定理即可求得多边形的边数.
(2)先根据三角形外角的性质求出∠EDB的度数,再由三角形内角和定理求出∠E的度数即可.
【解答】解:(1)设这个多边形的边数是n,
依题意得(n﹣2)×180°=3×360°﹣180°,
(n﹣2)=6﹣1,
n=7.
∴这个多边形的边数是7.
(2)∵∠EDB是△ADF的外角,∠1=38°,∠A=32°,
∴∠EDB=∠A+∠1=32°+38°=70°,
∵△EDB中,∠EDB=70°,∠B=70°,
∴∠E=180°﹣(∠B+∠EDB)=180°﹣(70°+70°)=40°.
【点评】本题考查的是三角形外角的性质,即三角形的一个外角等于和它不相邻的两个内角的和.
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2023/12/15 16:27:30;用户:陈振君;邮箱:18253
