15.1 轴对称图形 第3课时 课件(共14张PPT) 沪科版数学八年级上册
文档属性
| 名称 | 15.1 轴对称图形 第3课时 课件(共14张PPT) 沪科版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
15.1 轴对称图形
15.1.3 点的轴对称与坐标变化
第十五章 轴对称图形与等腰三角形
1.掌握在平面直角坐标系中关于x轴和y轴对称点的坐标变化规律.
2.能运用该规律解决画对称图形等简单的问题.
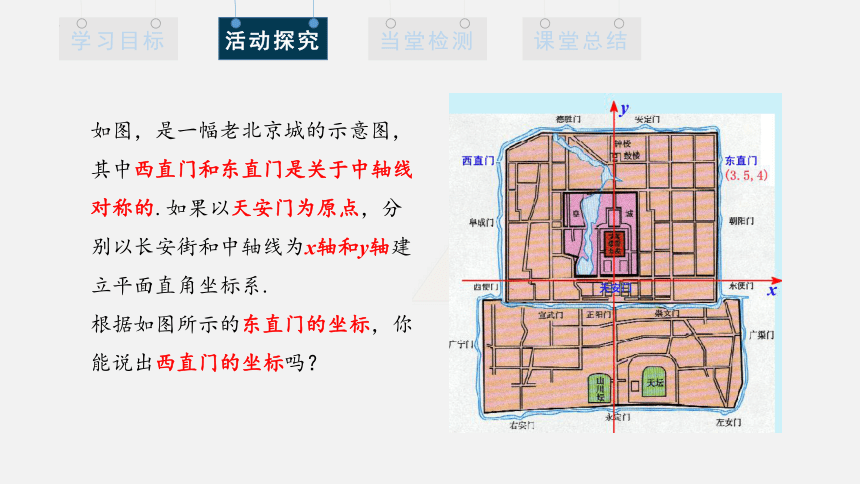
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.
根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
任务一:掌握在平面直角坐标系中对称点的坐标变化规律.
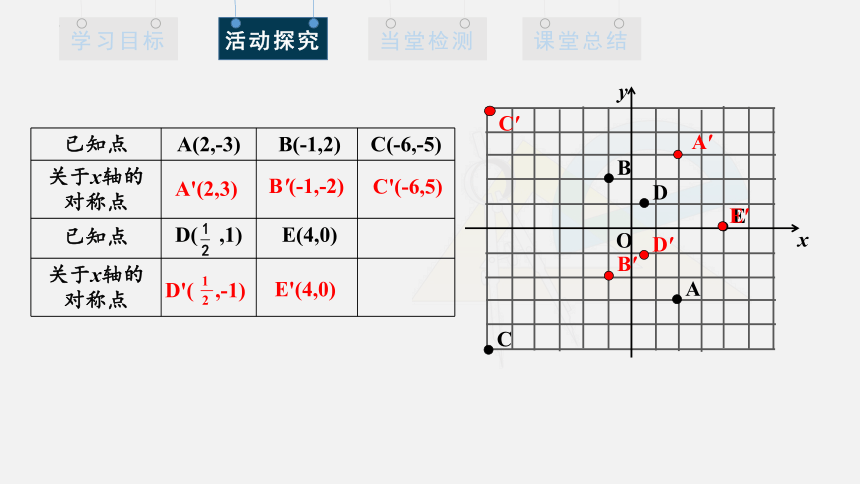
活动:在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,再和同学谈论一下.
已知点 A(2,-3) B(-1,2) C(-6,-5) D( , 1) E(4,0)
关于x轴的 对称点
关于y轴的 对称点
已知点 A(2,-3) B(-1,2) C(-6,-5)
关于x轴的对称点
已知点 D( ,1) E(4,0)
关于x轴的对称点
A'(2,3)
B'(-1,-2)
C'(-6,5)
D'( ,-1)
E'(4,0)
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
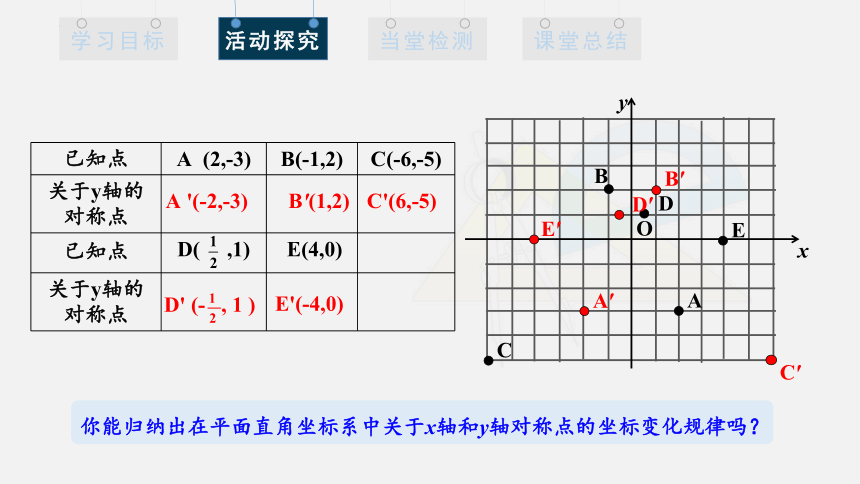
已知点 A (2,-3) B(-1,2) C(-6,-5)
关于y轴的 对称点
已知点 D( ,1) E(4,0)
关于y轴的 对称点
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
A '(-2,-3)
B'(1,2)
C'(6,-5)
D' (- , 1 )
E'(-4,0)
你能归纳出在平面直角坐标系中关于x轴和y轴对称点的坐标变化规律吗?
活动小结
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
(x , y)
关于 x 轴对称
(x , -y)
关于y轴对称的点的坐标的特点是:
纵坐标相等,横坐标互为相反数.
(简称:纵轴纵相等)
(x , y)
关于 y 轴对称
(-x , y)
练一练
关于x轴对称:
1.点P(-4, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.已知点A的坐标为(m,2),点B的坐标为(3,n),且点A与点B关于x轴对称,则m+n=_______.
关于y轴对称:
3.点P(-4, 6)与点Q关于y轴对称,则点Q的坐标为__________.
4.已知点A的坐标为(m,2),点B的坐标为(3,n),且点A与点B关于y轴对称,则m+n=_______.
(- 4 , -6 )
1
(4 , 6 )
-1
任务二:利用关于x轴或y轴对称的变化规律作轴对称图形.
活动:如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),
C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
O
D
C
A
B
A1
B1
D1
C1
A2
B2
D2
C2
解:①关于y轴对称,四边形ABCD四个顶点的横坐标互为相反数,纵坐标不变.②关于x轴对称,四边形ABCD四个顶点的纵坐标互为相反数,横坐标不变.
活动小结
1.在坐标系内作一个图形关于坐标轴的对称图形,只要先求出已知图形中的一些特殊点的对称点的坐标,例如多边形顶点;
2.描出并连接这些点,就可以得到这个图形关于坐标轴对称的图形.
1.点P关于x轴的对称点为(a,-1)关于y轴的对称点为(-2,b),那么点P的坐标是( )
A.(a,-b) B.(b,a)
C.(-1,-2) D.(2,1)
D
2.在平面直角坐标系内,点A(x-6,2y+1)与点B(2x,y-1)关于y轴对称,则x+y的值为( )
A.0 B.-1
C.2 D.-3
A
3.已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4,
解得a=2,b=-1.
∴点C(2,-1)在第四象限.
坐标系中图形
的轴对称图形
点的坐标P(x,y)
P1(x,-y)
P2(-x,y)
关于x轴对称
关于y轴对称
说一说你本堂课都学到了哪些知识?
15.1 轴对称图形
15.1.3 点的轴对称与坐标变化
第十五章 轴对称图形与等腰三角形
1.掌握在平面直角坐标系中关于x轴和y轴对称点的坐标变化规律.
2.能运用该规律解决画对称图形等简单的问题.
如图,是一幅老北京城的示意图,其中西直门和东直门是关于中轴线对称的.如果以天安门为原点,分别以长安街和中轴线为x轴和y轴建立平面直角坐标系.
根据如图所示的东直门的坐标,你能说出西直门的坐标吗?
任务一:掌握在平面直角坐标系中对称点的坐标变化规律.
活动:在平面直角坐标系中,画出下列已知点及其关于坐标轴的对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律,再和同学谈论一下.
已知点 A(2,-3) B(-1,2) C(-6,-5) D( , 1) E(4,0)
关于x轴的 对称点
关于y轴的 对称点
已知点 A(2,-3) B(-1,2) C(-6,-5)
关于x轴的对称点
已知点 D( ,1) E(4,0)
关于x轴的对称点
A'(2,3)
B'(-1,-2)
C'(-6,5)
D'( ,-1)
E'(4,0)
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 A (2,-3) B(-1,2) C(-6,-5)
关于y轴的 对称点
已知点 D( ,1) E(4,0)
关于y轴的 对称点
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
A '(-2,-3)
B'(1,2)
C'(6,-5)
D' (- , 1 )
E'(-4,0)
你能归纳出在平面直角坐标系中关于x轴和y轴对称点的坐标变化规律吗?
活动小结
关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
(简称:横轴横相等)
(x , y)
关于 x 轴对称
(x , -y)
关于y轴对称的点的坐标的特点是:
纵坐标相等,横坐标互为相反数.
(简称:纵轴纵相等)
(x , y)
关于 y 轴对称
(-x , y)
练一练
关于x轴对称:
1.点P(-4, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.已知点A的坐标为(m,2),点B的坐标为(3,n),且点A与点B关于x轴对称,则m+n=_______.
关于y轴对称:
3.点P(-4, 6)与点Q关于y轴对称,则点Q的坐标为__________.
4.已知点A的坐标为(m,2),点B的坐标为(3,n),且点A与点B关于y轴对称,则m+n=_______.
(- 4 , -6 )
1
(4 , 6 )
-1
任务二:利用关于x轴或y轴对称的变化规律作轴对称图形.
活动:如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),
C(-2,5),D(-5,4),分别画出与四边形ABCD关于y轴和x轴对称的图形.
x
y
O
D
C
A
B
A1
B1
D1
C1
A2
B2
D2
C2
解:①关于y轴对称,四边形ABCD四个顶点的横坐标互为相反数,纵坐标不变.②关于x轴对称,四边形ABCD四个顶点的纵坐标互为相反数,横坐标不变.
活动小结
1.在坐标系内作一个图形关于坐标轴的对称图形,只要先求出已知图形中的一些特殊点的对称点的坐标,例如多边形顶点;
2.描出并连接这些点,就可以得到这个图形关于坐标轴对称的图形.
1.点P关于x轴的对称点为(a,-1)关于y轴的对称点为(-2,b),那么点P的坐标是( )
A.(a,-b) B.(b,a)
C.(-1,-2) D.(2,1)
D
2.在平面直角坐标系内,点A(x-6,2y+1)与点B(2x,y-1)关于y轴对称,则x+y的值为( )
A.0 B.-1
C.2 D.-3
A
3.已知点A(2a+b,-4),B(3,a-2b)关于x轴对称,求点C(a,b)在第几象限?
解:∵点A(2a+b,-4),B(3,a-2b)关于x轴对称,
∴2a+b=3,a-2b=4,
解得a=2,b=-1.
∴点C(2,-1)在第四象限.
坐标系中图形
的轴对称图形
点的坐标P(x,y)
P1(x,-y)
P2(-x,y)
关于x轴对称
关于y轴对称
说一说你本堂课都学到了哪些知识?
