15.2 线段的垂直平分线 课件(共17张PPT) 沪科版数学八年级上册
文档属性
| 名称 | 15.2 线段的垂直平分线 课件(共17张PPT) 沪科版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:07:28 | ||
图片预览






文档简介
(共17张PPT)
第十五章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处才能使得它到三个小区的距离相等
1.能够通过尺规作图作一条已知线段的垂直平分线,
并能证明它的正确性;
2.理解线段的垂直平分线的性质定理及其逆定理;
任务一:通过尺规作图作一条已知线段的垂直平分线.
活动1:小组合作,完成下列问题.
做一做:
① 在半透明纸上画一条线段AB;
② 折纸使A与B重合,得到的折痕 l 就是线段AB的垂直平分线.
A
B
A
B
l
O
C
A(B)
l
O
想一想:
这样折纸怎么就是垂直平分线呢?
活动2:阅读课本P128尺规作图步骤,完成下列问题.
问题1:画弧的半径为什么要大于 的长?
问题2:为什么这样作出的直线EF,就是线段AB的垂直平分线呢?
问题3:尝试动手画图,作出线段的垂直平分线.
A
B
C
D
问题1:用大于 的长为半径画弧
目的是使两弧有交点.
问题3:
方法总结:我们也可以用这种方法确定线段的中点.
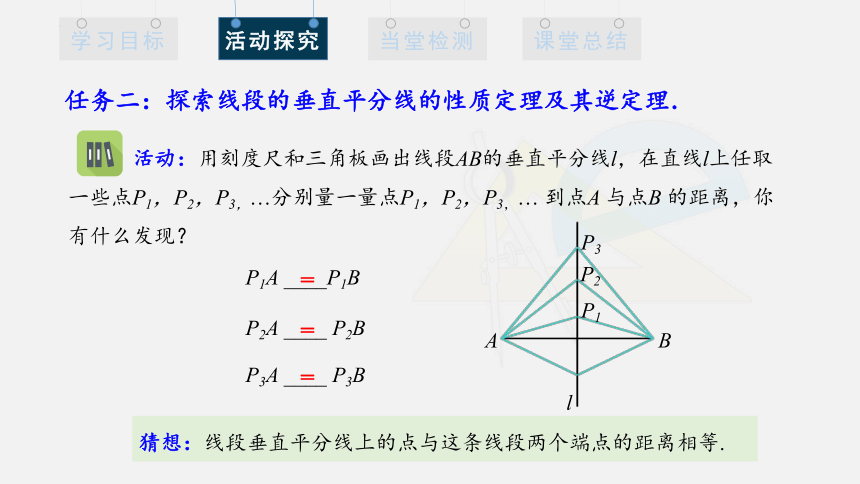
任务二:探索线段的垂直平分线的性质定理及其逆定理.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
活动:用刻度尺和三角板画出线段AB的垂直平分线l,在直线l上任取一些点P1,P2,P3,…分别量一量点P1,P2,P3,… 到点A 与点B 的距离,你有什么发现?
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
证明猜想:
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
应用格式:∵AC=BC,PC⊥AB,
P是l上任意一点,∴PA=PB.
P
A
B
l
C
活动小结
定理:线段垂直平分线上的点到线段两端的距离相等.
逆
命
题
逆命题:到线段两端距离相等的点在线段的垂直平分线上.
思考:写出下面定理的逆命题,它是真命题吗?如果是真命题,请给出证明.
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,PA =PB,PC =PC,
∴ Rt△PCA≌Rt△PCB(HL).∴ AC =BC.
又 PC⊥AB,∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.
验证命题:
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
应用格式:
∵PA =PB,∴点P 在AB 的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
P
A
B
活动小结
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC.
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC,
∴ PB = PC(等式性质)
∴ 点P在BC的垂直平分线上.
B
C
A
P
现在你能回答讲课前提出的问题吗?
你知道购物中心应该建在何处了吗?
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
活动小结
1.如图,AC=AD,BC=BD,则有( )
A. AB与CD互相垂直平分
B. CD垂直平分AB
C. AB垂直平分CD
D. CD平分∠ACB
C
2. 如图,△ABC中,AB = AC,AB的垂直平分线交AC于E,连接BE,
AB + BC = 16cm,则△BCE的周长是 cm.
16
A
B
C
D
E
A
B
C
D
E
3.已知:如图,AB=AC,DB=DC,E是AD上一点.求证:BE=CE
证明:连接BC,∵AB=AC,DB=DC,
∴点A、D在线段BC的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴AD是线段BC的垂直平分线,
∵点E在AD上,
∴BE=CE(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).
说说本节课你学到了什么?
第十五章 轴对称图形与等腰三角形
15.2 线段的垂直平分线
市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处才能使得它到三个小区的距离相等
1.能够通过尺规作图作一条已知线段的垂直平分线,
并能证明它的正确性;
2.理解线段的垂直平分线的性质定理及其逆定理;
任务一:通过尺规作图作一条已知线段的垂直平分线.
活动1:小组合作,完成下列问题.
做一做:
① 在半透明纸上画一条线段AB;
② 折纸使A与B重合,得到的折痕 l 就是线段AB的垂直平分线.
A
B
A
B
l
O
C
A(B)
l
O
想一想:
这样折纸怎么就是垂直平分线呢?
活动2:阅读课本P128尺规作图步骤,完成下列问题.
问题1:画弧的半径为什么要大于 的长?
问题2:为什么这样作出的直线EF,就是线段AB的垂直平分线呢?
问题3:尝试动手画图,作出线段的垂直平分线.
A
B
C
D
问题1:用大于 的长为半径画弧
目的是使两弧有交点.
问题3:
方法总结:我们也可以用这种方法确定线段的中点.
任务二:探索线段的垂直平分线的性质定理及其逆定理.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
活动:用刻度尺和三角板画出线段AB的垂直平分线l,在直线l上任取一些点P1,P2,P3,…分别量一量点P1,P2,P3,… 到点A 与点B 的距离,你有什么发现?
猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
证明猜想:
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
线段垂直平分线的性质:
线段垂直平分线上的点到线段两端的距离相等.
应用格式:∵AC=BC,PC⊥AB,
P是l上任意一点,∴PA=PB.
P
A
B
l
C
活动小结
定理:线段垂直平分线上的点到线段两端的距离相等.
逆
命
题
逆命题:到线段两端距离相等的点在线段的垂直平分线上.
思考:写出下面定理的逆命题,它是真命题吗?如果是真命题,请给出证明.
证明:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,PA =PB,PC =PC,
∴ Rt△PCA≌Rt△PCB(HL).∴ AC =BC.
又 PC⊥AB,∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
已知:如图,PA =PB.求证:点P 在线段AB 的垂直平分线上.
验证命题:
线段垂直平分线的判定:
到线段两端距离相等的点在线段的垂直平分线上.
应用格式:
∵PA =PB,∴点P 在AB 的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
P
A
B
活动小结
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC.
证明:连接PA,PB,PC.
∵点P在AB,AC的垂直平分线上,
∴PA=PB,PA=PC,
∴ PB = PC(等式性质)
∴ 点P在BC的垂直平分线上.
B
C
A
P
现在你能回答讲课前提出的问题吗?
你知道购物中心应该建在何处了吗?
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
活动小结
1.如图,AC=AD,BC=BD,则有( )
A. AB与CD互相垂直平分
B. CD垂直平分AB
C. AB垂直平分CD
D. CD平分∠ACB
C
2. 如图,△ABC中,AB = AC,AB的垂直平分线交AC于E,连接BE,
AB + BC = 16cm,则△BCE的周长是 cm.
16
A
B
C
D
E
A
B
C
D
E
3.已知:如图,AB=AC,DB=DC,E是AD上一点.求证:BE=CE
证明:连接BC,∵AB=AC,DB=DC,
∴点A、D在线段BC的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)
∴AD是线段BC的垂直平分线,
∵点E在AD上,
∴BE=CE(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).
说说本节课你学到了什么?
