数学人教A版(2019)必修第一册5.2.1三角函数的概念 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念 课件(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 49.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 21:31:13 | ||
图片预览








文档简介
(共34张PPT)
5.2 三角函数的概念
5.2.1 三角函数的概念
正弦
sin
赛银
撒银
散
塞硬
赛
余弦
cos
可撒银
考塞
天真
扣塞
阔赛银
正切
tan
疼怎
坦肩亭
汤挺
特恩泽
扩散
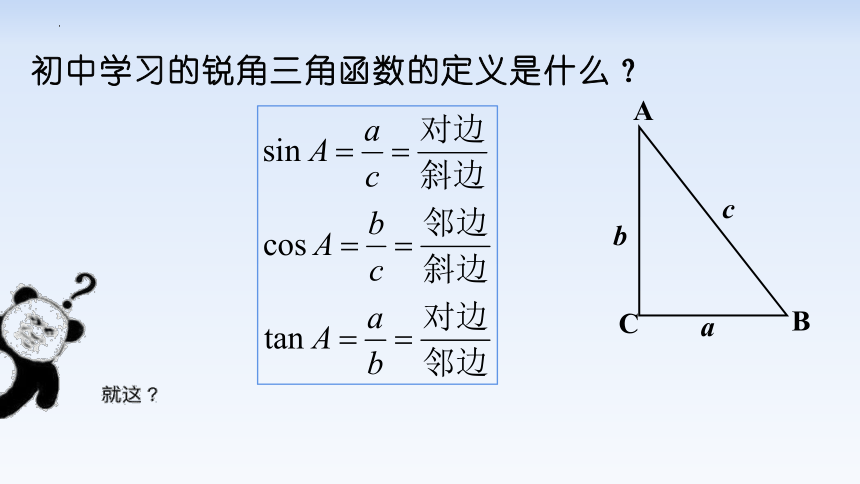
初中学习的锐角三角函数的定义是什么?
A
C
B
a
b
c
以单位圆的圆心O为原点,以射线OA为x轴的非负半轴,建立直角坐标系,点A的坐标为(1,0),点P的坐标为(x,y)射线OA从x轴的非负半轴开始,绕点O按逆时针方向旋转角α,终边位置为OP.
当时,P的坐标是什么?
当时,P的坐标是什么?是唯一确定的吗?
思考
?
利用勾股定理可以发现,
当时,点P的坐标是
当时,点P的坐标是
当时,点P的坐标是
都是唯一确定的.
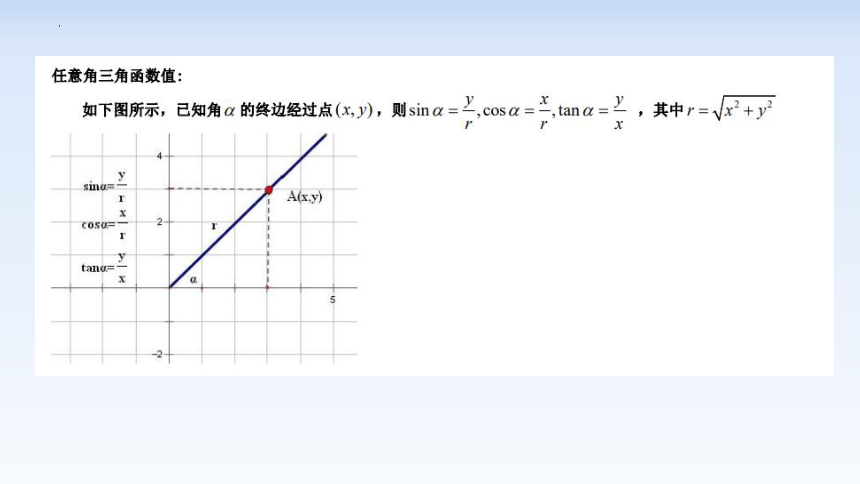
一般地,任意给定一个角α∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的.所以,点P的横坐标x、纵坐标y都是角α的函数.
PART 1 任意角的三角函数
设α是一个任意角,它的终边与单位圆的交点为点P(不与原点O重合),点P的坐标为(x,y)
(1)把点P的纵坐标y叫做角α的正弦函数:
(2)把点P的横坐标x叫做角α的余弦函数:
(3)把点P的纵坐标与横坐标的比值叫做角α的正切函数:
α
α
α
(x≠0)
特别注意
当时,角的终边在y轴上,这时点P的横坐标为0,所以α无意义.
PART 1 任意角的三角函数
按照函数常用的符号,将函数记为
(1)正弦函数:
(2)余弦函数:
(3)正切函数:
x
x
x
统称为三角函数.
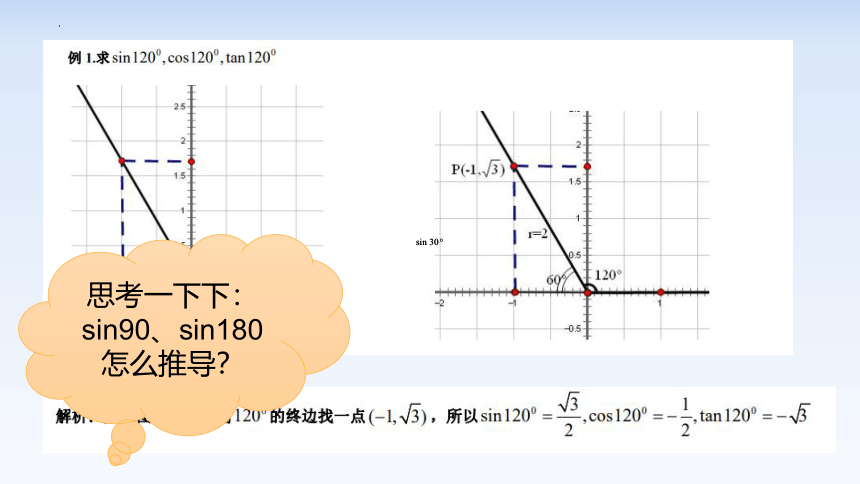
思考一下下:sin90、sin180怎么推导?
(1)三角函数值是比值,是一个实数.
(2)三角函数值的大小只与角的大小有关.
注意点:
例题探究 P175
例1 求的正弦、余弦和正切值.
例1
利用三角函数的定义求一个角的三角函数值有以下几种情况
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值.
(4)若已知角α终边上的点的坐标含参数,则需进行分类讨论.
跟踪训练1
√
√
解得x2=1,∴x=±1.
解得x2=1,又x<0,∴x=-1.
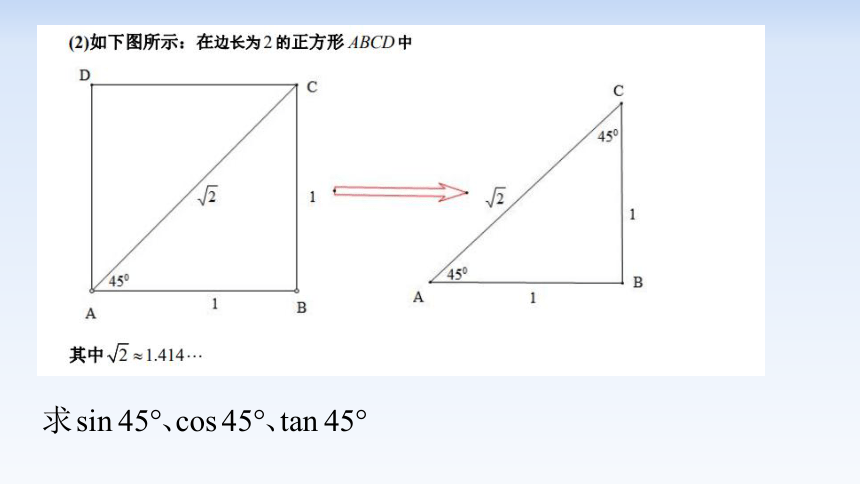
PART 3 特殊角的三角函数值
角α 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0
sina
cosa
tana
0
1
0
1
1
0
/
0
-1
-1
0
PART 2 三角函数值的正负
根据三角函数的定义,请将三角函数值的符号填入下图:
x
y
O
( ) ( )
( ) ( )
x
y
O
( ) ( )
( ) ( )
x
y
O
( ) ( )
( ) ( )
α
α
α
2.口诀:“一全正,二正弦,三正切,四余弦”.
例2
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
√
由sin αtan α<0可知sin α,tan α异号,从而α是第二或第三象限角.
综上可知,α是第三象限角.
(2)(多选)下列选项中,符号为负的是
A.sin(-100°) B.cos(-220°)
C.tan 10 D.cos π
√
√
√
已知点P(sin α,cos α)在第三象限,则角α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
跟踪训练2
√
∵点P(sin α,cos α)在第三象限,
判断三角函数值符号的两个步骤
(1)定象限:确定角α所在的象限.
(2)定符号:利用三角函数值的符号规律,即“一全正,二正弦,三正切,四余弦”来判断.
诱导公式一
终边相同的角的三角函数值什么关系?
思考
?
α+2π
与角α终边相同的角:
提示 由三角函数的定义,可以知道,终边相同的角的同一三角函数的值相等.
PART 1 诱导公式一
其中
三角函数值有“周而复始”的变化规律,即角α的终边每绕原点旋转一周,函数值将重复出现.
例题探究--求三角函数值
例1 求下列三角函数值
(1) (2) (3)
练习1 求下列三角函数值
(1) (2) (3)
练习巩固--求三角函数值
利用诱导公式一进行化简求值的步骤
(1)定形:将已知的任意角写成α+2kπ(k∈Z)的形式,其中α∈[0,2π).
(2)转化:根据诱导公式一,转化为求角α的某个三角函数值.
(3)求值:若角为特殊角,可直接求出该角的三角函数值.
计算下列各式的值:
(1)tan 405°-sin 450°+cos 750°;
跟踪训练3
原式=tan(360°+45°)-sin(360°+90°)+cos(2×360°+30°)
=tan 45°-sin 90°+cos 30°
课堂
小结
1.知识清单:
(1)三角函数的定义及求法.
(2)三角函数值在各象限内的符号.
(3)诱导公式一.
2.方法归纳:由特殊到一般、转化与化归、分类讨论.
3.常见误区:三角函数值的大小只与角的大小有关,与终边上的点无关;正切函数的定义域为
作业来噜~布鲁biu'布鲁biu~
完成校本作业27
5.2 三角函数的概念
5.2.1 三角函数的概念
正弦
sin
赛银
撒银
散
塞硬
赛
余弦
cos
可撒银
考塞
天真
扣塞
阔赛银
正切
tan
疼怎
坦肩亭
汤挺
特恩泽
扩散
初中学习的锐角三角函数的定义是什么?
A
C
B
a
b
c
以单位圆的圆心O为原点,以射线OA为x轴的非负半轴,建立直角坐标系,点A的坐标为(1,0),点P的坐标为(x,y)射线OA从x轴的非负半轴开始,绕点O按逆时针方向旋转角α,终边位置为OP.
当时,P的坐标是什么?
当时,P的坐标是什么?是唯一确定的吗?
思考
?
利用勾股定理可以发现,
当时,点P的坐标是
当时,点P的坐标是
当时,点P的坐标是
都是唯一确定的.
一般地,任意给定一个角α∈R,它的终边OP与单位圆交点P的坐标,无论是横坐标x还是纵坐标y,都是唯一确定的.所以,点P的横坐标x、纵坐标y都是角α的函数.
PART 1 任意角的三角函数
设α是一个任意角,它的终边与单位圆的交点为点P(不与原点O重合),点P的坐标为(x,y)
(1)把点P的纵坐标y叫做角α的正弦函数:
(2)把点P的横坐标x叫做角α的余弦函数:
(3)把点P的纵坐标与横坐标的比值叫做角α的正切函数:
α
α
α
(x≠0)
特别注意
当时,角的终边在y轴上,这时点P的横坐标为0,所以α无意义.
PART 1 任意角的三角函数
按照函数常用的符号,将函数记为
(1)正弦函数:
(2)余弦函数:
(3)正切函数:
x
x
x
统称为三角函数.
思考一下下:sin90、sin180怎么推导?
(1)三角函数值是比值,是一个实数.
(2)三角函数值的大小只与角的大小有关.
注意点:
例题探究 P175
例1 求的正弦、余弦和正切值.
例1
利用三角函数的定义求一个角的三角函数值有以下几种情况
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值.
(4)若已知角α终边上的点的坐标含参数,则需进行分类讨论.
跟踪训练1
√
√
解得x2=1,∴x=±1.
解得x2=1,又x<0,∴x=-1.
PART 3 特殊角的三角函数值
角α 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0
sina
cosa
tana
0
1
0
1
1
0
/
0
-1
-1
0
PART 2 三角函数值的正负
根据三角函数的定义,请将三角函数值的符号填入下图:
x
y
O
( ) ( )
( ) ( )
x
y
O
( ) ( )
( ) ( )
x
y
O
( ) ( )
( ) ( )
α
α
α
2.口诀:“一全正,二正弦,三正切,四余弦”.
例2
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
√
由sin αtan α<0可知sin α,tan α异号,从而α是第二或第三象限角.
综上可知,α是第三象限角.
(2)(多选)下列选项中,符号为负的是
A.sin(-100°) B.cos(-220°)
C.tan 10 D.cos π
√
√
√
已知点P(sin α,cos α)在第三象限,则角α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
跟踪训练2
√
∵点P(sin α,cos α)在第三象限,
判断三角函数值符号的两个步骤
(1)定象限:确定角α所在的象限.
(2)定符号:利用三角函数值的符号规律,即“一全正,二正弦,三正切,四余弦”来判断.
诱导公式一
终边相同的角的三角函数值什么关系?
思考
?
α+2π
与角α终边相同的角:
提示 由三角函数的定义,可以知道,终边相同的角的同一三角函数的值相等.
PART 1 诱导公式一
其中
三角函数值有“周而复始”的变化规律,即角α的终边每绕原点旋转一周,函数值将重复出现.
例题探究--求三角函数值
例1 求下列三角函数值
(1) (2) (3)
练习1 求下列三角函数值
(1) (2) (3)
练习巩固--求三角函数值
利用诱导公式一进行化简求值的步骤
(1)定形:将已知的任意角写成α+2kπ(k∈Z)的形式,其中α∈[0,2π).
(2)转化:根据诱导公式一,转化为求角α的某个三角函数值.
(3)求值:若角为特殊角,可直接求出该角的三角函数值.
计算下列各式的值:
(1)tan 405°-sin 450°+cos 750°;
跟踪训练3
原式=tan(360°+45°)-sin(360°+90°)+cos(2×360°+30°)
=tan 45°-sin 90°+cos 30°
课堂
小结
1.知识清单:
(1)三角函数的定义及求法.
(2)三角函数值在各象限内的符号.
(3)诱导公式一.
2.方法归纳:由特殊到一般、转化与化归、分类讨论.
3.常见误区:三角函数值的大小只与角的大小有关,与终边上的点无关;正切函数的定义域为
作业来噜~布鲁biu'布鲁biu~
完成校本作业27
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
