1.5.2 有理数的除法 课件(共17张PPT) 沪科版数学七年级上册
文档属性
| 名称 | 1.5.2 有理数的除法 课件(共17张PPT) 沪科版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 605.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:12:58 | ||
图片预览





文档简介
(共17张PPT)
第一章 有理数
1.5 有理数的乘除
2.有理数的除法
1.理解并能灵活运用有理数的除法法则,能熟练地进行除法运算;(重点)
2.知道有理数的除法可以转化为乘法运算。
一、学习目标
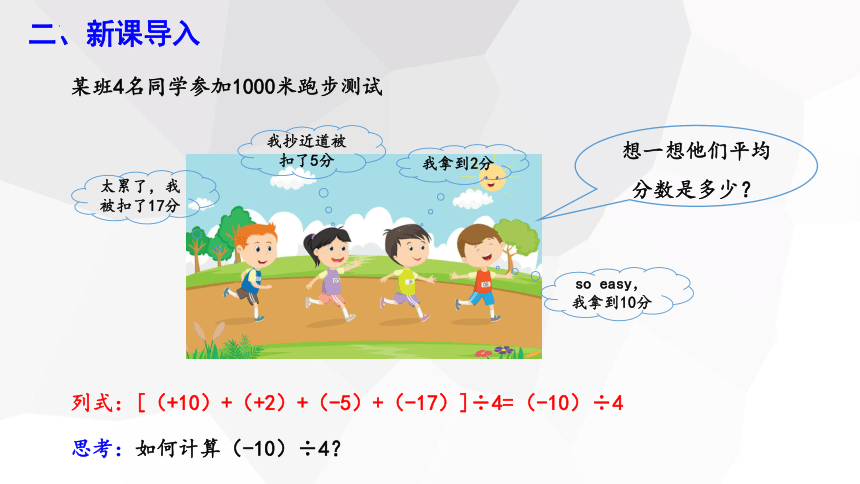
二、新课导入
某班4名同学参加1000米跑步测试
列式:[(+10)+(+2)+(-5)+(-17)]÷4=
(-10)÷4
思考:如何计算(-10)÷4?
so easy,我拿到10分
我拿到2分
我抄近道被扣了5分
太累了,我被扣了17分
想一想他们平均分数是多少?
我们要计算(-10)÷4
根据除法的意义,这就是说要求一个数,使它与4相乘等于-10
因为(-2.5)×4=-10,所以(-10)÷4=-2.5
又因为(-10)× =-2.5,所以(-10)× =(-10)÷4
三、概念剖析
下面我们来试着计算一些简单的式子.
试一试1:计算
(1)(-18)÷6= . (2)(-8)÷(-4)= .
(3)(-3)÷ = . (4) 0÷(-1)= .
三、概念剖析
2
思考:观察上面算式以及计算结果,你有什么发现
0
-6
-3
三、概念剖析
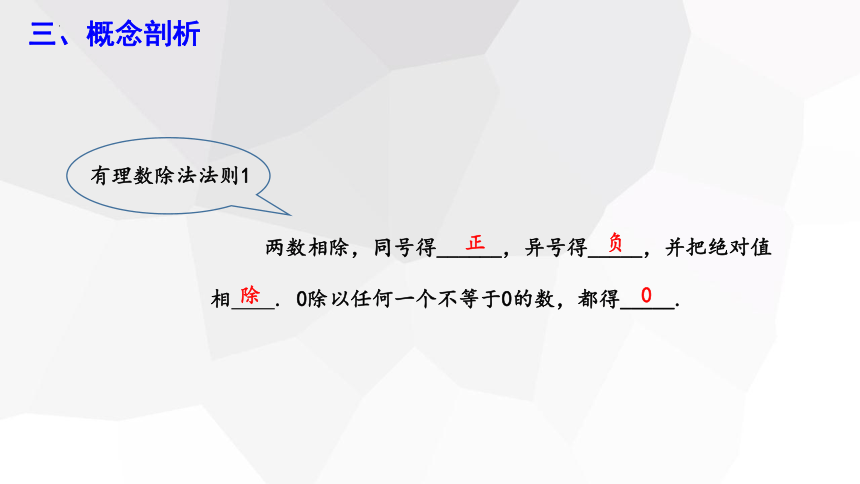
两数相除,同号得______,异号得_____,并把绝对值相 . 0除以任何一个不等于0的数,都得_____.
正
负
0
除
有理数除法法则1
试一试2:计算
(1)5÷(-2)= . 5×( )= .
(2)(-3)÷(-1)= . (-3)×(-1)= .
(3)3÷( )= . 3×( )= .
(4)4÷0=?
三、概念剖析
3
3
无意义,除数不能为0
思考:通过以上几例除法与乘法式子的比较,你能得到什么结论
-10
-10
三、概念剖析
有理数除法法则2
除以一个不等于0的数,等于乘以这个数的倒数
这个法则也可以表示成
a÷b=a· (b≠0)
例1.选用适当的法则进行计算.
(1)(-3)÷0.25 (2)( )÷
(3) 14÷(-7) (4)0÷(-6)
解:
(1)原式=(-3)×4
=-12
(2)原式=( )×
=-3
(3)原式=-(14÷7)
=-2
(4)原式=0
四、典型例题
四、典型例题
分析:根据有理数的除法法则,并选择合适的法则进行计算即可.
例2.计算-3÷6÷( )÷( ).
解:原式=-(3÷6)÷( )÷( )
= ÷( )÷( )
=+( ÷ )÷( )
=1×(-3)
=-3
1.计算(1)(-27)÷9 (2)4÷(-0.125)
解:(1)(-27)÷9
(2)4÷(-0.125)
【当堂检测】
=-(27÷9)
=-3
=4×(-8)
=-32
解:(1)原式=(-2)÷(-2)
(2)原式=4÷(-3)÷6
【当堂检测】
2.计算(1)(-18)÷9÷(-2) (2)4÷( )÷6
=1
=-12÷6
= -2
四、典型例题
例3. 两个有理数的商为正数,和为负数,这两个数的符号是( )
A.一正一负 B.都是负数
C.都是正数 D.不能确定
B
解:从选项入手,
当这两个数是一正一负时,商为负数,和不能确定,排除A;
当这两个数都是负数时,商为正数,和为负数;
当这两个数都是正数时,商为正数,和为正数,排除C;
故选B.
总结:判断有理数正负属性时,往往可以从选项入手;如果是非选择题,则需要分情况讨论:一正一负2种情况,都是正1种情况,都是负1种情况,共4种情况,切忌遗漏,需全面分析。
四、典型例题
【当堂检测】
3.两数的商为正数,那么这两个数( ).
A.和为正 B.差为正
C.积为正 D.以上都不对
C
4.下面结论中正确的有( ).
①若一个负数比它的倒数大,则这个负数的范围在-1与0之间
②若两数和为正,商为负,则这两个数异号,且负数的绝对值较小
③0除以任何数都得0
④任何整数都大于它的倒数
A.1个 B.2个 C.3个 D.4个
【当堂检测】
B
五、课堂总结
有理数除法法则
法则1:除以一个不等于0的数,等于乘以这个数的倒数;
这个法则也可以表示成
法则2:两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数.
a÷b=a· (b≠0).
第一章 有理数
1.5 有理数的乘除
2.有理数的除法
1.理解并能灵活运用有理数的除法法则,能熟练地进行除法运算;(重点)
2.知道有理数的除法可以转化为乘法运算。
一、学习目标
二、新课导入
某班4名同学参加1000米跑步测试
列式:[(+10)+(+2)+(-5)+(-17)]÷4=
(-10)÷4
思考:如何计算(-10)÷4?
so easy,我拿到10分
我拿到2分
我抄近道被扣了5分
太累了,我被扣了17分
想一想他们平均分数是多少?
我们要计算(-10)÷4
根据除法的意义,这就是说要求一个数,使它与4相乘等于-10
因为(-2.5)×4=-10,所以(-10)÷4=-2.5
又因为(-10)× =-2.5,所以(-10)× =(-10)÷4
三、概念剖析
下面我们来试着计算一些简单的式子.
试一试1:计算
(1)(-18)÷6= . (2)(-8)÷(-4)= .
(3)(-3)÷ = . (4) 0÷(-1)= .
三、概念剖析
2
思考:观察上面算式以及计算结果,你有什么发现
0
-6
-3
三、概念剖析
两数相除,同号得______,异号得_____,并把绝对值相 . 0除以任何一个不等于0的数,都得_____.
正
负
0
除
有理数除法法则1
试一试2:计算
(1)5÷(-2)= . 5×( )= .
(2)(-3)÷(-1)= . (-3)×(-1)= .
(3)3÷( )= . 3×( )= .
(4)4÷0=?
三、概念剖析
3
3
无意义,除数不能为0
思考:通过以上几例除法与乘法式子的比较,你能得到什么结论
-10
-10
三、概念剖析
有理数除法法则2
除以一个不等于0的数,等于乘以这个数的倒数
这个法则也可以表示成
a÷b=a· (b≠0)
例1.选用适当的法则进行计算.
(1)(-3)÷0.25 (2)( )÷
(3) 14÷(-7) (4)0÷(-6)
解:
(1)原式=(-3)×4
=-12
(2)原式=( )×
=-3
(3)原式=-(14÷7)
=-2
(4)原式=0
四、典型例题
四、典型例题
分析:根据有理数的除法法则,并选择合适的法则进行计算即可.
例2.计算-3÷6÷( )÷( ).
解:原式=-(3÷6)÷( )÷( )
= ÷( )÷( )
=+( ÷ )÷( )
=1×(-3)
=-3
1.计算(1)(-27)÷9 (2)4÷(-0.125)
解:(1)(-27)÷9
(2)4÷(-0.125)
【当堂检测】
=-(27÷9)
=-3
=4×(-8)
=-32
解:(1)原式=(-2)÷(-2)
(2)原式=4÷(-3)÷6
【当堂检测】
2.计算(1)(-18)÷9÷(-2) (2)4÷( )÷6
=1
=-12÷6
= -2
四、典型例题
例3. 两个有理数的商为正数,和为负数,这两个数的符号是( )
A.一正一负 B.都是负数
C.都是正数 D.不能确定
B
解:从选项入手,
当这两个数是一正一负时,商为负数,和不能确定,排除A;
当这两个数都是负数时,商为正数,和为负数;
当这两个数都是正数时,商为正数,和为正数,排除C;
故选B.
总结:判断有理数正负属性时,往往可以从选项入手;如果是非选择题,则需要分情况讨论:一正一负2种情况,都是正1种情况,都是负1种情况,共4种情况,切忌遗漏,需全面分析。
四、典型例题
【当堂检测】
3.两数的商为正数,那么这两个数( ).
A.和为正 B.差为正
C.积为正 D.以上都不对
C
4.下面结论中正确的有( ).
①若一个负数比它的倒数大,则这个负数的范围在-1与0之间
②若两数和为正,商为负,则这两个数异号,且负数的绝对值较小
③0除以任何数都得0
④任何整数都大于它的倒数
A.1个 B.2个 C.3个 D.4个
【当堂检测】
B
五、课堂总结
有理数除法法则
法则1:除以一个不等于0的数,等于乘以这个数的倒数;
这个法则也可以表示成
法则2:两数相除,同号得正,异号得负,并把绝对值相除;
0除以任何一个不等于0的数.
a÷b=a· (b≠0).
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
