4.3线段的长短比较 课件(共21张PPT)2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 4.3线段的长短比较 课件(共21张PPT)2023—2024学年沪科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 839.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:14:12 | ||
图片预览






文档简介
(共21张PPT)
第四章 直线与角
4.3 线段的长短比较
一、学习目标
1.会借助直尺、圆规等工具比较两条线段的长短.
2.会用数学语言描述线段中点,会解决有关线段中点的问题.
3.能在具体情境中体会两点之间线段最短的性质,知道两点间距离的概念.(重点)
二、新课导入
如果我们要比较长颈鹿和小马的身高,该怎么办呢?
三、概念剖析
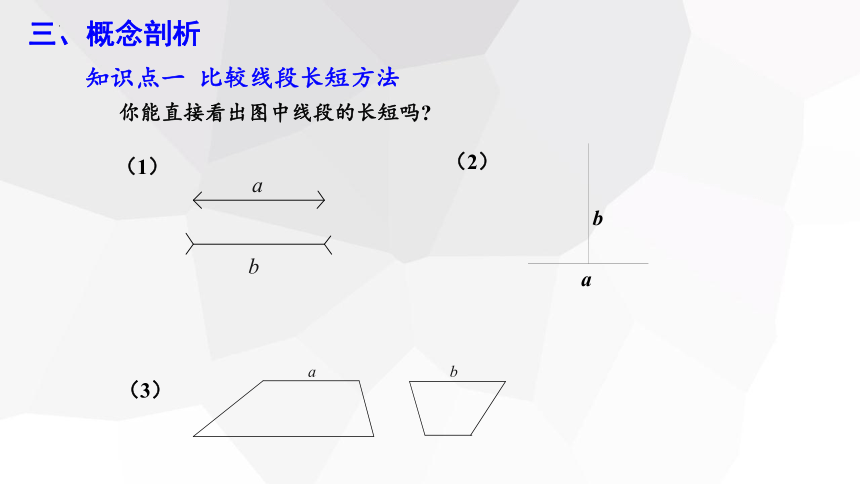
(1)
b
(2)
a
(3)
你能直接看出图中线段的长短吗
知识点一 比较线段长短方法
三、概念剖析
(1)度量法:即用一把尺量出两条线段的长度,再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.2cm
1
2
3
5
4
6
7
8
0
归纳总结:线段的比较
三、概念剖析
(2)叠合法:先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较线段的大小.
A
B
D
C
(1)如果点B在C、D之间,
记作ABA
B
D
C
(2)如果点B在线段CD延 长线上,记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
三、概念剖析
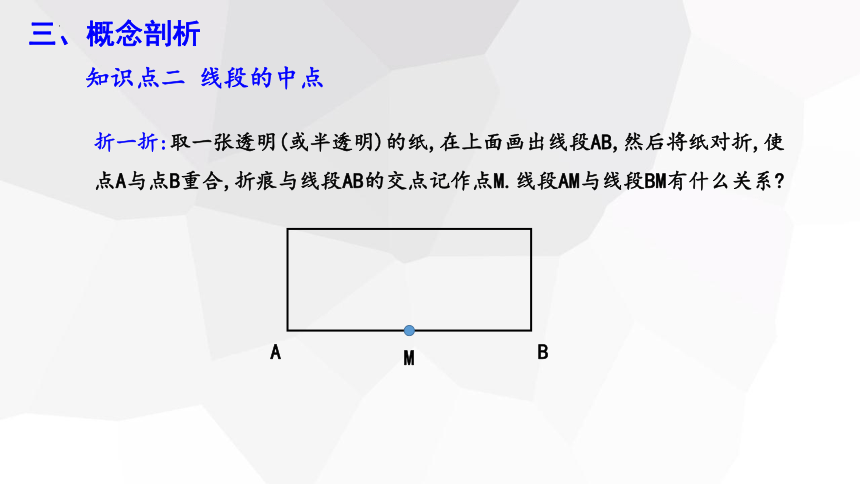
知识点二 线段的中点
折一折:取一张透明(或半透明)的纸,在上面画出线段AB,然后将纸对折,使点A与点B重合,折痕与线段AB的交点记作点M.线段AM与线段BM有什么关系
A
B
M
三、概念剖析
请描述一下线段中点的概念(对照图形)
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
中点定义
数学语言:
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
三、概念剖析
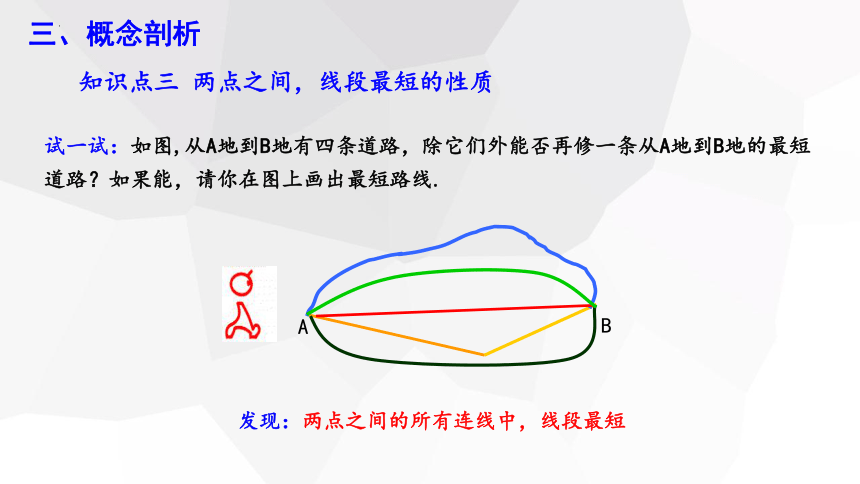
试一试:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
知识点三 两点之间,线段最短的性质
A
B
发现:两点之间的所有连线中,线段最短
我们把两点之间线段的长度,叫做这两点之间的距离.
上述发现可以总结为:
两点之间,线段最短
三、概念剖析
草坪上被踩出了一条小路,在这里,从A地到B地,人们为什么不走大路走小路?
因为从草坪中穿过比从马路上走近 .
三、概念剖析
四、典型例题
例1:怎样画一条线段等于已知线段?
画一条线段AB=线段a。
a
方法一:
先用刻度尺量出线段a的长度,
再画一条等于这个长度的线段AB.
方法二:
尺规作图
作法:
(1)作射线AC;
(2)在射线AC上截取AB = a
则线段AB就是所求作的线段.
A
C
B
四、典型例题
尺规作图的应用注意事项
1.先画一条射线;
2.按作图要求用圆规截长 ;
3.以射线的端点为圆心,圆规所截长度为半径作弧 ;
4.不可以使用刻度尺度量 .
5.作出结论(∴线段即为所求) .
【当堂检测】
1.已知:线段m、n(如图)
求作:线段AC,使AC = m + n.
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段.
(2)在射线AM上顺次截取AB = m,BC = n.
例2.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
四、典型例题
解:(1)因为点M是线段AC的中点,点N是线段BC的中点;
所以BC=2NC,AC=2AM=12cm,
所以2NC=BC=AB-AC=8cm,故NC=4cm.
(2)因为点M是线段AC的中点,点N是线段BC的中点;
(2)如果MN=6 cm,求AB的长.
所以BC=2NC,AC=2CM;
所以AB=AC+BC=2CM+2CN=2(CM+CN)=2MN=12cm
四、典型例题
注意:计算线段长短的方法一般有两种:第一是逐段计算,主要围绕线段的和、差、倍、分关系展开.第二是整体转化,线段转化为两条线段的和或差,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
【当堂检测】
2.根据图形填空:
(1)AB= + ;
D
(2)AB= + = + = + + ;
(3)CD= - = - =
- - .
AC CB
AD DB
AC CB
AC CD DB
AD AC
CB DB
AB AC DB
(4)AD=AB-____=AC+ _____
BD
CD
3.已知线段AB=4,C为直线AB上的一点,D为线段AC的中点,且BC=3,求线段AD的长度 .
【当堂检测】
解:因为AB=4,BC=3;
所以AC=AB-BC=1;
又因为D为AC的中点;
所以AD= AC=
四、典型例题
例3.A、B、C三点在同一条直线上,A、B两点之间的距离为9cm,B、C两点之间的距离为5cm,则A、C两点之间的距离是多少
解:(1)当点C在线段AB的延长线上(如图1)时,AC=AB+BC=14 cm;
(2)当点C在线段AB上(如图2)时,AC=AB-BC=4 cm.
注意:分类讨论思想是解题关键所在,切记不能遗漏任何一种情况。
4.有线段AB=12cm,点O是线段AB中点,点C是直线AB上一点,且AC= BC,P是线段AC的中点,线段OP的长为( )cm.
【当堂检测】
A.4 B.12 C.4或12 D.不确定
C
五、课堂总结
1.比较线段长短的方法有度量法和叠合法.度量法一般用直尺测量,叠合法一般使用圆规.
定义:点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
2.中点
数学语言:
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
3.两点之间,线段最短.两点之间线段的长度,叫做这两点之间的距离.
第四章 直线与角
4.3 线段的长短比较
一、学习目标
1.会借助直尺、圆规等工具比较两条线段的长短.
2.会用数学语言描述线段中点,会解决有关线段中点的问题.
3.能在具体情境中体会两点之间线段最短的性质,知道两点间距离的概念.(重点)
二、新课导入
如果我们要比较长颈鹿和小马的身高,该怎么办呢?
三、概念剖析
(1)
b
(2)
a
(3)
你能直接看出图中线段的长短吗
知识点一 比较线段长短方法
三、概念剖析
(1)度量法:即用一把尺量出两条线段的长度,再进行比较.
1
2
3
5
4
6
7
8
0
3.1cm
4.2cm
1
2
3
5
4
6
7
8
0
归纳总结:线段的比较
三、概念剖析
(2)叠合法:先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置来比较线段的大小.
A
B
D
C
(1)如果点B在C、D之间,
记作AB
B
D
C
(2)如果点B在线段CD延 长线上,记作AB>CD
(3)如果点B与点D重合,
记作AB=CD
A
B
C
D
三、概念剖析
知识点二 线段的中点
折一折:取一张透明(或半透明)的纸,在上面画出线段AB,然后将纸对折,使点A与点B重合,折痕与线段AB的交点记作点M.线段AM与线段BM有什么关系
A
B
M
三、概念剖析
请描述一下线段中点的概念(对照图形)
点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
中点定义
数学语言:
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
三、概念剖析
试一试:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请你在图上画出最短路线.
知识点三 两点之间,线段最短的性质
A
B
发现:两点之间的所有连线中,线段最短
我们把两点之间线段的长度,叫做这两点之间的距离.
上述发现可以总结为:
两点之间,线段最短
三、概念剖析
草坪上被踩出了一条小路,在这里,从A地到B地,人们为什么不走大路走小路?
因为从草坪中穿过比从马路上走近 .
三、概念剖析
四、典型例题
例1:怎样画一条线段等于已知线段?
画一条线段AB=线段a。
a
方法一:
先用刻度尺量出线段a的长度,
再画一条等于这个长度的线段AB.
方法二:
尺规作图
作法:
(1)作射线AC;
(2)在射线AC上截取AB = a
则线段AB就是所求作的线段.
A
C
B
四、典型例题
尺规作图的应用注意事项
1.先画一条射线;
2.按作图要求用圆规截长 ;
3.以射线的端点为圆心,圆规所截长度为半径作弧 ;
4.不可以使用刻度尺度量 .
5.作出结论(∴线段即为所求) .
【当堂检测】
1.已知:线段m、n(如图)
求作:线段AC,使AC = m + n.
m
n
作法:
(1)作射线AM;
A
M
B
C
则线段AC就是所求作的线段.
(2)在射线AM上顺次截取AB = m,BC = n.
例2.如图所示,点C是线段AB上一点,点M是线段AC的中点,点N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
四、典型例题
解:(1)因为点M是线段AC的中点,点N是线段BC的中点;
所以BC=2NC,AC=2AM=12cm,
所以2NC=BC=AB-AC=8cm,故NC=4cm.
(2)因为点M是线段AC的中点,点N是线段BC的中点;
(2)如果MN=6 cm,求AB的长.
所以BC=2NC,AC=2CM;
所以AB=AC+BC=2CM+2CN=2(CM+CN)=2MN=12cm
四、典型例题
注意:计算线段长短的方法一般有两种:第一是逐段计算,主要围绕线段的和、差、倍、分关系展开.第二是整体转化,线段转化为两条线段的和或差,然后再通过线段的中点的等量关系进行替换,将未知线段转化为已知线段.
【当堂检测】
2.根据图形填空:
(1)AB= + ;
D
(2)AB= + = + = + + ;
(3)CD= - = - =
- - .
AC CB
AD DB
AC CB
AC CD DB
AD AC
CB DB
AB AC DB
(4)AD=AB-____=AC+ _____
BD
CD
3.已知线段AB=4,C为直线AB上的一点,D为线段AC的中点,且BC=3,求线段AD的长度 .
【当堂检测】
解:因为AB=4,BC=3;
所以AC=AB-BC=1;
又因为D为AC的中点;
所以AD= AC=
四、典型例题
例3.A、B、C三点在同一条直线上,A、B两点之间的距离为9cm,B、C两点之间的距离为5cm,则A、C两点之间的距离是多少
解:(1)当点C在线段AB的延长线上(如图1)时,AC=AB+BC=14 cm;
(2)当点C在线段AB上(如图2)时,AC=AB-BC=4 cm.
注意:分类讨论思想是解题关键所在,切记不能遗漏任何一种情况。
4.有线段AB=12cm,点O是线段AB中点,点C是直线AB上一点,且AC= BC,P是线段AC的中点,线段OP的长为( )cm.
【当堂检测】
A.4 B.12 C.4或12 D.不确定
C
五、课堂总结
1.比较线段长短的方法有度量法和叠合法.度量法一般用直尺测量,叠合法一般使用圆规.
定义:点M把线段AB分成相等的两条线段AM和BM,点M叫做线段AB的中点.
2.中点
数学语言:
因为M是线段AB的中点
所以AM= MB = AB
(或AB=2AM=2MB)
3.两点之间,线段最短.两点之间线段的长度,叫做这两点之间的距离.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
