4.4角课件(共21张PPT)2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 4.4角课件(共21张PPT)2023—2024学年沪科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 668.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:13:27 | ||
图片预览







文档简介
(共21张PPT)
4.4 角
第四章 直线与角
一、学习目标
1.通过丰富的实例,认识角,明确角的两种定义与四种表示方法.
2.初步了解锐角、直角、钝角、平角、周角的定义.
3.知道角的度量单位,并能进行度、分、秒的简单换算及加减乘除运算.
A
B
C
.
.
.
二、新课导入
生活中有许许多多与角有关的事例.
二、新课导入
角的定义有两种:
1.角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
因为射线是向一方无限延伸的,所以我们画出的角,只是角的一部分.
三、概念剖析
2.角的第二定义:角也可以看成是由一条射线绕它的端点旋转而成的.
一条射线绕它的端点旋转,当终边和始边成一条直线时(180°),所成的角叫做平角;终边继续旋转,当它又和始边重合时(360°),所成的角叫做周角.
三、概念剖析
3.讨论:角的大小与角的两条边的长短有关系吗
没有.
角的表示方法:
(1)用三个大写字母;如∠ABC;
(2)用一个大写字母,如∠A;
(3)用一个数字加弧线,弧线表示该角的范围,如∠1;
(4)用一个希腊字母加弧线,弧线表示该角的范围,如∠α.
角通常用符号“∠”表示,读作“角”.
三、概念剖析
B
A
C
B
A
D
C
⑴
⑵
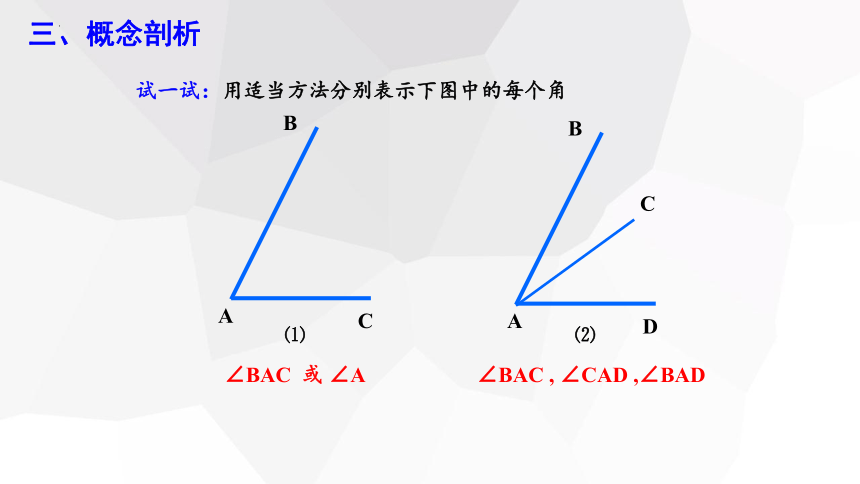
试一试:用适当方法分别表示下图中的每个角
∠BAC 或 ∠A
∠BAC , ∠CAD ,∠BAD
三、概念剖析
三、概念剖析
钟表上,60秒钟是1分钟,60分钟是1小时,这种计算方法,我们称为60进制,同样的,角度中的度、分、秒也是60进制.
1周角=360°,1平角=180°,1直角=90°,1'= °,1'= 60″ ,1″= '.
例题1:如图
(1)写出能用一个字母表示的角;
(2)写出以B为顶点的角;
分析:本题目主要考查角的表示方法,从角的顶点去思考有几个角是解决此题的关键.
四、典型例题
解:(1)∠A,∠C;
(2)∠ABE,∠ABC,∠EBC;
四、典型例题
(3)共有7个小于平角的角,
分别是:以A为顶点的是∠A,
以B为顶点的是∠ABE、∠ABC、∠EBC,
以C为顶点的是∠C,以E为顶点的是∠AEB、∠CEB.
(3)图中共有几个小于平角的角
注意:角的表示方法要恰当选取,特别是在同一顶点处不止一个角时,注意正确表示.
1.如图,下列表示角的方法中,正确的是( )
A.∠C B.AEF C.∠B D.∠E
C
【当堂检测】
【当堂检测】
2.如图,下列说法正确的是( )
A.∠BAC和∠DAE是不同的两个角
B.∠ABC和∠ACB是同一个角
C.∠ADE就是∠D
D.∠ABC可以用∠B表示
D
四、典型例题
例题2:(1)把36.28°化成度、分、秒;
(2)把51°28′30″化成度.
分析:根据1°=60′,1′=60″,先把30秒化为分,再把分化为度,逐级计算.
解:(1)36.28°=36°16′48″
(2)30″=30÷60=0.5′;
所以28′30″=28.5′=28.5÷60=0.475°
所以51°28′30″=51.475°
四、典型例题
例题3:计算下列各式:①28°39′38″+52°43′56″;②30°31′×5
解:①原式=(28°+52°)+( 39′+43′)+( 38″+56″)
=80°+82′+94″
=81°23′34″.
②30°31′×5= 30°×5+31′×5
=150°+155′
=150°+2°35′=152°35′.
方法归纳:度分秒的加法:度与度、分与分、秒与秒分别相加,计算结束后,满60进1.乘、除法运算可以按分配律来进行,不够除可以把余数化为低位的再除.
【当堂检测】
3.下列各式中,角度互化正确的是( )
A. 18°18′18″=18.33° B. 46°48′=46.48°
C. 22.25°=22°15′ D. 28.5°=28°50′
C
【当堂检测】
4.计算:①90°-28°12′; ②143°16′÷4.
解:①90°-28°12′=89°60′-28°12′
=(89°-28°)+(60′-12′)
=61°48′ .
②143°16′÷4=143°÷4+16′÷4
=35°+3°÷4+16′÷4
=35°+(180′+16′)÷4
=35°+49′=35°49′.
方法归纳:度分秒的减法:度与度、分与分、秒与秒分别相减,如果不够减,就向前一位借1,借1°就相当于借60',借1'就相当于借60″.
四、典型例题
例题4:由1时15分到1时54分,时钟的分针、时针各转了多少度?在1时54分时,时钟的分针、时针夹角为多少度(小于180°的角)?
分析:把时钟的针看成一个以它的中心为顶点的周角,分针每60分转了360°,因而每分转360°÷60= 6°.时针每时转动5个格共30°.计算第二问时还有其他方法.
解:从1时15分到1时54分,分针共走了54分-15分=39分.
分针转动的度数为6°×39=234°.
时针转动的度数为39÷60×30°=19.5°.
四、典型例题
在1时54分时,时针与分针的夹角如图,
点评:正确画出钟表示意图是解决问题的关键,时针与分针所夹角的度数是所经过的路径形成的度数.
所以小于180°的夹角为57°+36°=93°.
【当堂检测】
5.(1)8时15分,时针与分针的夹角是多少?
(2)从12时整始,至少再过多少时间,分针与时针再一次重合?
解:(1)8时15分,时针与分针的夹角为8×30°+15×0.5°-15×6°=157.5°.
(2)设至少再过x分钟分针与时针再一次重合,
根据题意得x·0.5°+360°=x·6°,解得x=
答:从12时整始,至少再过 分钟,分针与时针再一次重合。
1.角的两种定义:
2.角的表示方法有四种:用三个大写字母表示;用一个大写字母表示;用一个希腊字母或一个阿拉伯数字表示.
五、课堂总结
(1)角是由两条具有公共端点的射线组成的.
(2)角也可以看成是由一条射线绕它的端点旋转而成的.
3.角的单位(度、分、秒)及其换算(60进制).
4.4 角
第四章 直线与角
一、学习目标
1.通过丰富的实例,认识角,明确角的两种定义与四种表示方法.
2.初步了解锐角、直角、钝角、平角、周角的定义.
3.知道角的度量单位,并能进行度、分、秒的简单换算及加减乘除运算.
A
B
C
.
.
.
二、新课导入
生活中有许许多多与角有关的事例.
二、新课导入
角的定义有两种:
1.角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
因为射线是向一方无限延伸的,所以我们画出的角,只是角的一部分.
三、概念剖析
2.角的第二定义:角也可以看成是由一条射线绕它的端点旋转而成的.
一条射线绕它的端点旋转,当终边和始边成一条直线时(180°),所成的角叫做平角;终边继续旋转,当它又和始边重合时(360°),所成的角叫做周角.
三、概念剖析
3.讨论:角的大小与角的两条边的长短有关系吗
没有.
角的表示方法:
(1)用三个大写字母;如∠ABC;
(2)用一个大写字母,如∠A;
(3)用一个数字加弧线,弧线表示该角的范围,如∠1;
(4)用一个希腊字母加弧线,弧线表示该角的范围,如∠α.
角通常用符号“∠”表示,读作“角”.
三、概念剖析
B
A
C
B
A
D
C
⑴
⑵
试一试:用适当方法分别表示下图中的每个角
∠BAC 或 ∠A
∠BAC , ∠CAD ,∠BAD
三、概念剖析
三、概念剖析
钟表上,60秒钟是1分钟,60分钟是1小时,这种计算方法,我们称为60进制,同样的,角度中的度、分、秒也是60进制.
1周角=360°,1平角=180°,1直角=90°,1'= °,1'= 60″ ,1″= '.
例题1:如图
(1)写出能用一个字母表示的角;
(2)写出以B为顶点的角;
分析:本题目主要考查角的表示方法,从角的顶点去思考有几个角是解决此题的关键.
四、典型例题
解:(1)∠A,∠C;
(2)∠ABE,∠ABC,∠EBC;
四、典型例题
(3)共有7个小于平角的角,
分别是:以A为顶点的是∠A,
以B为顶点的是∠ABE、∠ABC、∠EBC,
以C为顶点的是∠C,以E为顶点的是∠AEB、∠CEB.
(3)图中共有几个小于平角的角
注意:角的表示方法要恰当选取,特别是在同一顶点处不止一个角时,注意正确表示.
1.如图,下列表示角的方法中,正确的是( )
A.∠C B.AEF C.∠B D.∠E
C
【当堂检测】
【当堂检测】
2.如图,下列说法正确的是( )
A.∠BAC和∠DAE是不同的两个角
B.∠ABC和∠ACB是同一个角
C.∠ADE就是∠D
D.∠ABC可以用∠B表示
D
四、典型例题
例题2:(1)把36.28°化成度、分、秒;
(2)把51°28′30″化成度.
分析:根据1°=60′,1′=60″,先把30秒化为分,再把分化为度,逐级计算.
解:(1)36.28°=36°16′48″
(2)30″=30÷60=0.5′;
所以28′30″=28.5′=28.5÷60=0.475°
所以51°28′30″=51.475°
四、典型例题
例题3:计算下列各式:①28°39′38″+52°43′56″;②30°31′×5
解:①原式=(28°+52°)+( 39′+43′)+( 38″+56″)
=80°+82′+94″
=81°23′34″.
②30°31′×5= 30°×5+31′×5
=150°+155′
=150°+2°35′=152°35′.
方法归纳:度分秒的加法:度与度、分与分、秒与秒分别相加,计算结束后,满60进1.乘、除法运算可以按分配律来进行,不够除可以把余数化为低位的再除.
【当堂检测】
3.下列各式中,角度互化正确的是( )
A. 18°18′18″=18.33° B. 46°48′=46.48°
C. 22.25°=22°15′ D. 28.5°=28°50′
C
【当堂检测】
4.计算:①90°-28°12′; ②143°16′÷4.
解:①90°-28°12′=89°60′-28°12′
=(89°-28°)+(60′-12′)
=61°48′ .
②143°16′÷4=143°÷4+16′÷4
=35°+3°÷4+16′÷4
=35°+(180′+16′)÷4
=35°+49′=35°49′.
方法归纳:度分秒的减法:度与度、分与分、秒与秒分别相减,如果不够减,就向前一位借1,借1°就相当于借60',借1'就相当于借60″.
四、典型例题
例题4:由1时15分到1时54分,时钟的分针、时针各转了多少度?在1时54分时,时钟的分针、时针夹角为多少度(小于180°的角)?
分析:把时钟的针看成一个以它的中心为顶点的周角,分针每60分转了360°,因而每分转360°÷60= 6°.时针每时转动5个格共30°.计算第二问时还有其他方法.
解:从1时15分到1时54分,分针共走了54分-15分=39分.
分针转动的度数为6°×39=234°.
时针转动的度数为39÷60×30°=19.5°.
四、典型例题
在1时54分时,时针与分针的夹角如图,
点评:正确画出钟表示意图是解决问题的关键,时针与分针所夹角的度数是所经过的路径形成的度数.
所以小于180°的夹角为57°+36°=93°.
【当堂检测】
5.(1)8时15分,时针与分针的夹角是多少?
(2)从12时整始,至少再过多少时间,分针与时针再一次重合?
解:(1)8时15分,时针与分针的夹角为8×30°+15×0.5°-15×6°=157.5°.
(2)设至少再过x分钟分针与时针再一次重合,
根据题意得x·0.5°+360°=x·6°,解得x=
答:从12时整始,至少再过 分钟,分针与时针再一次重合。
1.角的两种定义:
2.角的表示方法有四种:用三个大写字母表示;用一个大写字母表示;用一个希腊字母或一个阿拉伯数字表示.
五、课堂总结
(1)角是由两条具有公共端点的射线组成的.
(2)角也可以看成是由一条射线绕它的端点旋转而成的.
3.角的单位(度、分、秒)及其换算(60进制).
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
