4.6用尺规作图线段与角课件(共17张PPT) 2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 4.6用尺规作图线段与角课件(共17张PPT) 2023—2024学年沪科版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:10:05 | ||
图片预览





文档简介
(共17张PPT)
第四章 直线与角
4.6 用尺规作图线段与角
1.知道尺规作图的基本方法和要求,能用语言表述尺规作图的过程
2.会用尺规作图作一条线段等于已知线段
3.会用尺规作图作一个角等于已知角
一、学习目标
二、新课导入
你能用一个圆规和一把没有刻度的直尺,画出这些美丽的图案吗?
(一)尺规作图
三、概念剖析
在几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
画图形、设计图案,时常要画线段和角.
一些复杂的尺规作图都是由基本作图组成的.
下面介绍两种基本作图:
(1)用尺规作一条线段等于已知线段;
(2)作一个角等于已知角.
三、概念剖析
(二)作一条线段等于已知线段
已知:线段AB.
求作:线段A′B′,使A′B′=AB.
A
B
三、概念剖析
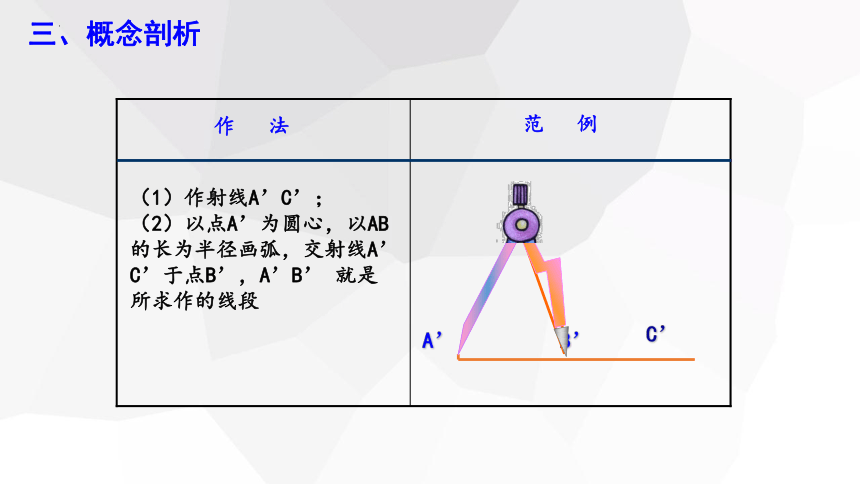
(1)作射线A’C’;
(2)以点A’为圆心,以AB的长为半径画弧,交射线A’ C’于点B’,A’B’ 就是所求作的线段
A’
B’
C’
作 法
范 例
三、概念剖析
(三)作一个角等于已知角
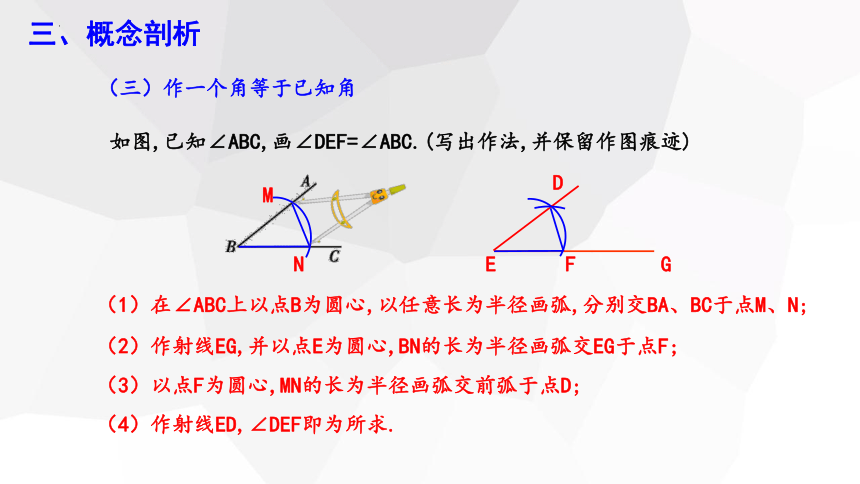
如图,已知∠ABC,画∠DEF=∠ABC.(写出作法,并保留作图痕迹)
(1)在∠ABC上以点B为圆心,以任意长为半径画弧,分别交BA、BC于点M、N;
(2)作射线EG,并以点E为圆心,BN的长为半径画弧交EG于点F;
(3)以点F为圆心,MN的长为半径画弧交前弧于点D;
(4)作射线ED,∠DEF即为所求.
M
N
E
F
D
G
三、概念剖析
尺规作图的一般步骤:
(1)已知,即:已知的条件是什么.
(2)求作,即:所要作的最终的结果是什么,满足什么条件.
(3)分析,即:分析如何作出所要求作的图形,一般不用写出来.
(4)作法,这是作图的主要步骤,在这里要写清作图的过程.有时候不要求写作法,但一定要保留作图的痕迹.
四、典型例题
例1.下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线L的直线
D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α
解析:认识到尺规作图是用没有刻度的直尺和圆规来画图和掌握作图语言的表述就能够排除错误选项解题了。A、画线段MN=3cm,需要知道长度,而尺规作图中的直尺是没有长度的,错误;B、用量角器画出∠AOB的平分线,量角器不在尺规作图的工具里,错误;C、用三角尺作过点A垂直于直线L的直线,三角尺也不在作图工具里,错误;D、正确.
故选D.
D
【当堂检测】
1.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
D
【当堂检测】
2.下列属于尺规作图的是( )
A.用刻度尺和圆规作△ABC B.用量角器画一个300度的角
C.用圆规画半径2cm的圆 D.作一条线段等于已知线段
D
四、典型例题
例2.如图,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.
解:作法:如图,
(1)作射线AF;
(2)在射线AF上顺次截取AB=BC=a,CD=b;
(3)在线段AD上截取DE=c.
所以线段AE即为所求.
A
F
B
C
D
a
a
b
c
E
四、典型例题
归纳总结
用尺规作图,首先要弄明白所作的是什么图形,要作这个图形应从哪里入手.一些复杂的图形都是由简单的基本作图得到的.求作几条线段的和时,线段之和与所画线段的顺序无关,求作线段的差时,要注意向相反的方向截取要减去的线段 .
【当堂检测】
3.已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
b
C
b
A
D
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
a
B
四、典型例题
例3.如图,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.
解:作法:如图,
①作射线OA;
②以射线OA为一边作∠AOC=∠α;
③以O为顶点,以射线OC为一边,
在∠AOC的内部作∠AOB=∠β,
则∠BOC就是所求作的角.
A
O
C
α
β
α-β
B
复杂图形都是由简单图形转化得出,比如倍数关系可以转化为几个这样的线段或者角相加的和
【当堂检测】
4.已知: ∠1, ∠2
求作:∠3,使得∠3= ∠2-∠1
1
2
解:作法:
(1)作射线OA;
(2)以OA为边做∠AOB=∠1;
(3)以O为顶点,以射线OA为边,
在∠AOB内部作∠AOD=∠2.
则∠BOD即为所求的∠3.
O
A
B
D
五、课堂总结
1.几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
2.作一条线段等于已知线段和线段的和、差、倍、分关系的画法
3.作一个角等于已知角和角的和、差、倍、分关系的画法
第四章 直线与角
4.6 用尺规作图线段与角
1.知道尺规作图的基本方法和要求,能用语言表述尺规作图的过程
2.会用尺规作图作一条线段等于已知线段
3.会用尺规作图作一个角等于已知角
一、学习目标
二、新课导入
你能用一个圆规和一把没有刻度的直尺,画出这些美丽的图案吗?
(一)尺规作图
三、概念剖析
在几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
画图形、设计图案,时常要画线段和角.
一些复杂的尺规作图都是由基本作图组成的.
下面介绍两种基本作图:
(1)用尺规作一条线段等于已知线段;
(2)作一个角等于已知角.
三、概念剖析
(二)作一条线段等于已知线段
已知:线段AB.
求作:线段A′B′,使A′B′=AB.
A
B
三、概念剖析
(1)作射线A’C’;
(2)以点A’为圆心,以AB的长为半径画弧,交射线A’ C’于点B’,A’B’ 就是所求作的线段
A’
B’
C’
作 法
范 例
三、概念剖析
(三)作一个角等于已知角
如图,已知∠ABC,画∠DEF=∠ABC.(写出作法,并保留作图痕迹)
(1)在∠ABC上以点B为圆心,以任意长为半径画弧,分别交BA、BC于点M、N;
(2)作射线EG,并以点E为圆心,BN的长为半径画弧交EG于点F;
(3)以点F为圆心,MN的长为半径画弧交前弧于点D;
(4)作射线ED,∠DEF即为所求.
M
N
E
F
D
G
三、概念剖析
尺规作图的一般步骤:
(1)已知,即:已知的条件是什么.
(2)求作,即:所要作的最终的结果是什么,满足什么条件.
(3)分析,即:分析如何作出所要求作的图形,一般不用写出来.
(4)作法,这是作图的主要步骤,在这里要写清作图的过程.有时候不要求写作法,但一定要保留作图的痕迹.
四、典型例题
例1.下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线L的直线
D.已知∠α,用没有刻度的直尺和圆规作∠AOB,使∠AOB=2∠α
解析:认识到尺规作图是用没有刻度的直尺和圆规来画图和掌握作图语言的表述就能够排除错误选项解题了。A、画线段MN=3cm,需要知道长度,而尺规作图中的直尺是没有长度的,错误;B、用量角器画出∠AOB的平分线,量角器不在尺规作图的工具里,错误;C、用三角尺作过点A垂直于直线L的直线,三角尺也不在作图工具里,错误;D、正确.
故选D.
D
【当堂检测】
1.尺规作图的画图工具是( )
A.刻度尺、量角器 B.三角板、量角器
C.直尺、量角器 D.没有刻度的直尺和圆规
D
【当堂检测】
2.下列属于尺规作图的是( )
A.用刻度尺和圆规作△ABC B.用量角器画一个300度的角
C.用圆规画半径2cm的圆 D.作一条线段等于已知线段
D
四、典型例题
例2.如图,已知线段a、b、c,用圆规和直尺画线段,使它等于2a+b-c.
解:作法:如图,
(1)作射线AF;
(2)在射线AF上顺次截取AB=BC=a,CD=b;
(3)在线段AD上截取DE=c.
所以线段AE即为所求.
A
F
B
C
D
a
a
b
c
E
四、典型例题
归纳总结
用尺规作图,首先要弄明白所作的是什么图形,要作这个图形应从哪里入手.一些复杂的图形都是由简单的基本作图得到的.求作几条线段的和时,线段之和与所画线段的顺序无关,求作线段的差时,要注意向相反的方向截取要减去的线段 .
【当堂检测】
3.已知线段a,b画一条线段c,使它的长度等于两条已知线段的长度的和.
a
b
C
b
A
D
画法:
1.画射线AD
2.用圆规在射线AD上截取AB=a
3.用圆规在射线BD上截取BC=b
线段AC就是所求的线段
a
B
四、典型例题
例3.如图,已知∠α和∠β(∠α>∠β),求作∠AOB,使∠AOB=∠α-∠β.
解:作法:如图,
①作射线OA;
②以射线OA为一边作∠AOC=∠α;
③以O为顶点,以射线OC为一边,
在∠AOC的内部作∠AOB=∠β,
则∠BOC就是所求作的角.
A
O
C
α
β
α-β
B
复杂图形都是由简单图形转化得出,比如倍数关系可以转化为几个这样的线段或者角相加的和
【当堂检测】
4.已知: ∠1, ∠2
求作:∠3,使得∠3= ∠2-∠1
1
2
解:作法:
(1)作射线OA;
(2)以OA为边做∠AOB=∠1;
(3)以O为顶点,以射线OA为边,
在∠AOB内部作∠AOD=∠2.
则∠BOD即为所求的∠3.
O
A
B
D
五、课堂总结
1.几何中,通常用没有刻度的直尺和圆规来画图,这种画图的方法叫做尺规作图.
2.作一条线段等于已知线段和线段的和、差、倍、分关系的画法
3.作一个角等于已知角和角的和、差、倍、分关系的画法
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
