第六章 整式的运算单元素养综合检测试题(含解析)
文档属性
| 名称 | 第六章 整式的运算单元素养综合检测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 355.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北京课改版数学七年级下册
第六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.计算a·a-1(a≠0)的结果为( )
A.-1 B.0 C.1 D.-a
2.(2023安徽中考)下列计算正确的是( )
A.a4+a4=a8 B.a4·a4=a16
C.(a4)4=a16 D.a8÷a4=a2
3.(2021北京海淀期中)若式子(x-2)0有意义,则有理数x的取值范围是( )
A.x≠2 B.x=2 C.x≠0 D.x=0
4.【新独家原创】下列式子:①(a-3)(-a+3);②(2x+y)(2x-y);③(a+2b+c)(a-2b+c);④(-x+y)(x+y);⑤(n-m)(-m+n);⑥(a2-b)(a-b2).其中可运用平方差公式计算的有( )
A.2个 B.3个
C.4个 D.5个
5.下列计算中错误的是( )
A.4a5b3c2÷(-2a2bc)2=ab
B.(a+1)(a-1)(a2+1)=a4-1
C.4x2y·÷4x2y2=-
D.25×=x2-x+1
6.(2023北京十三中模拟)如果x2+2x-2=0,那么代数式x(x+2)+(x+1)2的值是( )
A.-5 B.5 C.3 D.-3
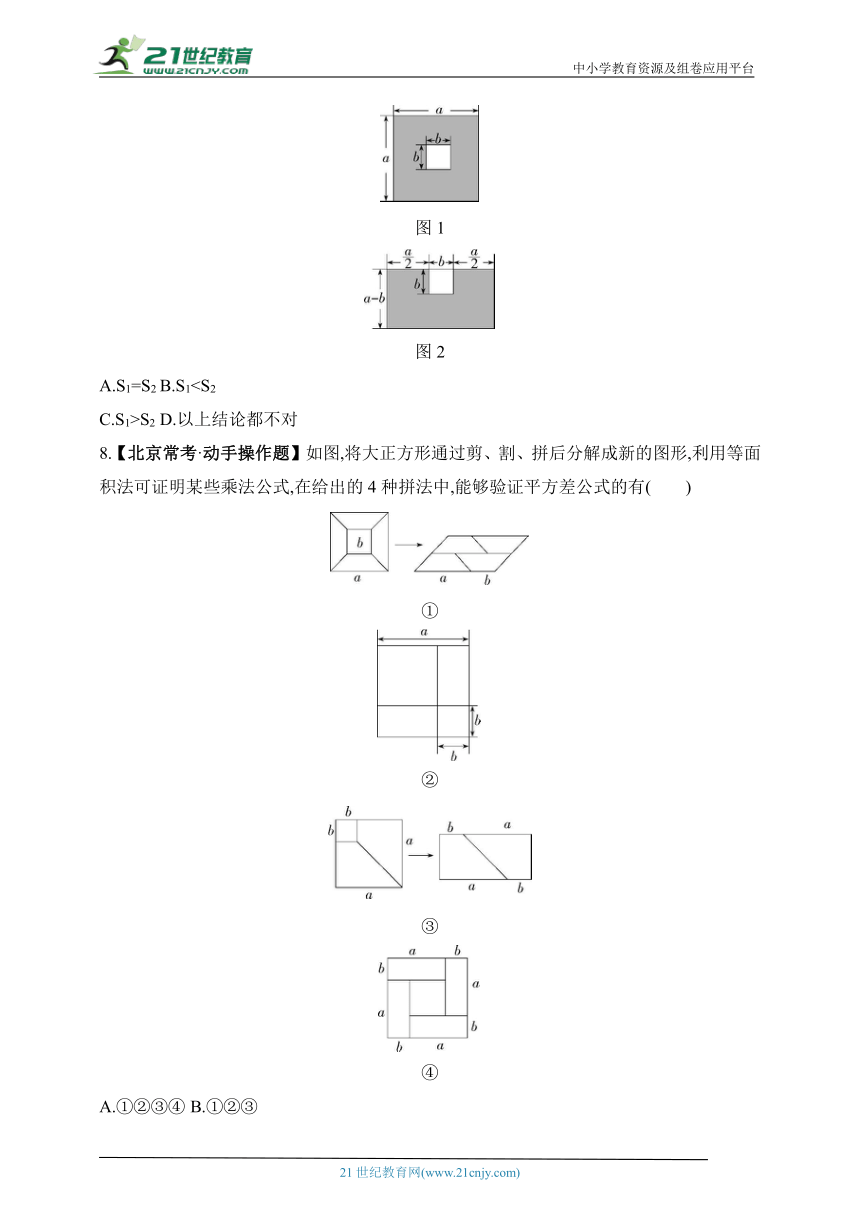
7.(2023北京八中期中)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为b的正方形花坛,学生会提出两个方案:
方案一:如图1,绕花坛搭建外围是正方形的“回”字形舞台(阴影部分),面积为S1;
方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),面积为S2.
具体数据如图所示,则S1与S2的大小关系为( )
图1
图2
A.S1=S2 B.S1C.S1>S2 D.以上结论都不对
8.【北京常考·动手操作题】如图,将大正方形通过剪、割、拼后分解成新的图形,利用等面积法可证明某些乘法公式,在给出的4种拼法中,能够验证平方差公式的有( )
①
②
③
④
A.①②③④ B.①②③
C.①③ D.③④
二、填空题(每小题3分,共18分)
9.(2023湖南常德中考)计算:(a2b)3= .
10.【新独家原创】计算(x2+2x+2)(x-2)-x(x2-1),并把结果按照字母x升幂排列: .
11.【新独家原创】【跨学科·物理】太阳内部高温核聚变反应释放的辐射能功率为3.8×1023千瓦,利用新型太阳能电池板可以将其中的50亿分之一转化为电能,按照一个家庭一年用电量1 000千瓦时,能满足一个中等城市760 000个家庭使用 年.
12.(2022四川德阳中考)已知(x+y)2=25,(x-y)2=9,则xy= .
13.(2021山东潍坊期末)若多项式A除以(2x2-3),得到的商式为3x-4,余式为5x+2,则A= .
14.(2022北京昌平一中期中)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
……
由此猜想(a+b)10的展开式中第三项的系数是 .
三、解答题(共58分)
15.(2023北京顺义期末)(6分)计算:
(1)(1-a)(1+a)+(a-a3)÷a;
(2)(2x2)3·x-8x4·x3.
16.(6分)用乘法公式计算:
(1)100×99;(2).
17.(2023北京平谷期末)(5分)已知x2-5x-4=0,求2x2-3(x2-2+x)-2的值.
18.(2023北京通州期中)(6分)某校有一块长为3a+b,宽为2a+b的长方形土地,计划将阴影部分进行绿化,空白正方形部分修建一座雕像,其中a>b>0.请用含a,b的代数式表示绿化部分的面积(结果化为最简形式).
19.(2022北京昌平一中期中)(7分)逆向运用幂的运算可以得到am+n=am·an,am-n=am÷an,amn=(am)n,ambm=(ab)m,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则常可化繁为简,化难为易,使问题巧妙得解.
(1)52 021×= ;
(2)若3×9m×27m=311,求m的值.
20.(8分)已知多项式A=(x+2)2+x(x-2)-(x+3)(x-3).
(1)化简多项式A时,小明的结果与其他同学的不同,请你检查小明同学的解题过程.
解:A=(x+2)2+x(x-2)-(x+3)(x-3) =x2+4+x2-x2=x2-5.
在标出①②③的三项中,出现错误的是 (填序号),请写出正确的解答过程.
(2)小亮说:“只要给出x2+2x+1的合理的值,即可求出多项式A的值.”小明给出x2+2x+1的值为4,请你求出此时A的值.
21.(2023北京东城期末)(10分)给出定义如下:我们称使等式a-b=ab+1成立的一对有理数a,b为“相伴有理数对”,记为(a,b).
(1)数对,中,是“相伴有理数对”的是 ;
(2)若(x+1,5)是“相伴有理数对”,则x的值是 ;
(3)若(a,b)是“相伴有理数对”,求3ab-a+(a+b-5ab)+1的值.
22.【数形结合思想】(2022四川成都实验学校期中)(10分)[知识生成]通常,用两种不同的方法计算同一个图形的面积可以得到一个恒等式.
例如:图1是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.请解答下列问题:
(1)观察图2,请你写出(a+b)2、(a-b)2、ab之间的等量关系: .
(2)根据(1)中的等量关系解决下列问题:
若x+y=6,xy=,求(x-y)2的值.
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积也可以得到一个恒等式.
(3)根据图3,写出一个代数恒等式: .
(4)已知a+b=3,ab=1,利用(3)中的式子求的值.
图1
图2
图3
答案全解全析
1.C a·a-1=a1-1=a0=1.
2.C (a4)4=a16.故选C.
3.A ∵式子(x-2)0有意义,∴x-2≠0,解得x≠2.故选A.
4.B (2x+y)(2x-y)、(a+2b+c)(a-2b+c)和(-x+y)(x+y)中,既有符号相同的项又有符号相反的项,符合平方差公式的特点,可运用平方差公式计算.故选B.
5.D 4a5b3c2÷(-2a2bc)2=4a5b3c2÷4a4b2c2=ab,故选项A计算正确;(a+1)(a-1)(a2+1)=(a2-1)·(a2+1)=a4-1,故选项B计算正确;4x2y·÷4x2y2=-,故选项C计算正确;25×=x2-x+25,故选项D计算错误,符合题意.故选D.
6.B x(x+2)+(x+1)2=x2+2x+x2+2x+1=2x2+4x+1,
∵x2+2x-2=0,∴x2+2x=2,
∴原式=2(x2+2x)+1=2×2+1=5,
故选B.
7.C ∵题图2中由花坛和阴影组成的长方形的长是a×2+b=a+b,宽是a-b,
∴S2=(a+b)(a-b)-b2=a2-2b2,
∵S1=a2-b2,
∴S1>S2.
故选C.
8.C ①可以验证的等式为a2-b2=(a+b)(a-b),可以验证平方差公式;②可以验证的等式为a2=(a-b)2+b2+2b(a-b),不能验证平方差公式;③可以验证的等式为a2-b2=(a+b)(a-b),可以验证平方差公式;④可以验证的等式为(a+b)2=(a-b)2+4ab,不能验证平方差公式.所以能够验证平方差公式的是①③.故选C.
9.答案 a6b3
解析 (a2b)3=(a2)3b3=a6b3.
10.答案 -4-x
解析 原式=x3-2x2+2x2-4x+2x-4-x3+x=-4-x.
11.答案 100 000
解析 3.8×1023÷(5×109)÷(103)÷(7.6×105)=105=100 000.
12.答案 4
解析 ∵(x+y)2=x2+y2+2xy=25,(x-y)2=x2+y2-2xy=9,∴(x+y)2-(x-y)2=4xy=16,∴xy=4.
13.答案 6x3-8x2-4x+14
解析 ∵多项式A除以(2x2-3),得到的商式为3x-4,余式为5x+2,
∴A=(2x2-3)(3x-4)+(5x+2)=6x3-8x2-9x+12+5x+2=6x3-8x2-4x+14.
14.答案 45
解析 (a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;
(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7;
(a+b)8的展开式的系数分别为1,8,28,56,70,56,28,8,1;
(a+b)9的展开式的系数分别为1,9,36,84,126,126,84,36,9,1;
(a+b)10的展开式的系数分别为1,10,45,120,210,252,210,120,45,10,1,
则(a+b)10的展开式中第三项的系数为45.
15.解析 (1)(1-a)(1+a)+(a-a3)÷a
=1-a2+1-a2
=2-2a2.
(2)(2x2)3·x-8x4·x3
=8x6·x-8x7
=8x7-8x7
=0.
16.解析 (1)100×99=×=1002-=9 999.
(2)==202+2×20×+=413.
17.解析 ∵x2-5x-4=0,
∴x2-5x=4,
∴2x2-3(x2-2+x)-2
=2x2-3x2+6-3x-2x+2x2-1
=x2-5x+5
=4+5
=9.
18.解析 由题意得,绿化部分的面积=(3a+b)(2a+b)-(a+2b)2=6a2+3ab+2ab+b2-a2-4b2-4ab=5a2+ab-3b2.
19.解析 (1)52 021×
=
=1.
(2)∵3×9m×27m=311,
∴3×32m×33m=311,
∴31+2m+3m=311,
∴1+2m+3m=11,
解得m=2.
20.解析 (1)A=(x+2)2+x(x-2)-(x+3)(x-3)
=x2+4x+4+x2-2x-x2+9
=x2+2x+13,
故出现错误的是①③.
(2)∵x2+2x+1=4,
∴x2+2x=3,∴A=x2+2x+13=3+13=16.
21解析 (1)当a=-2,b=时,
a-b=-2-=-,
ab+1=-2×+1=,
则a-b≠ab+1,
所以不是“相伴有理数对”.
当a=-,b=-3时,
a-b=--(-3)=-+3=,
ab+1=-×(-3)+1=,
则a-b=ab+1,
所以是“相伴有理数对”.
(2)∵(x+1,5)是“相伴有理数对”,
∴x+1-5=(x+1)×5+1,
解得x=-.
(3)3ab-a+(a+b-5ab)+1
=3ab-a+a+b-ab+1
=ab-a+b+1
=ab-(a-b)+1,
∵a-b=ab+1,
∴原式=ab-(ab+1)+1
=ab-ab-+1
=.
22.解析 (1)(a+b)2-(a-b)2=4ab(答案不唯一).
(2)由(1)可知(x+y)2-(x-y)2=4xy,
∵x+y=6,xy=,
∴(x-y)2=(x+y)2-4xy=36-4×=14.
(3)(a+b)3=a3+3a2b+3ab2+b3.
(4)由(3)可知a3+b3=(a+b)3-3a2b-3ab2=(a+b)3-3ab(a+b),
把a+b=3,ab=1代入得a3+b3=33-3×1×3=18.
∴=9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北京课改版数学七年级下册
第六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.计算a·a-1(a≠0)的结果为( )
A.-1 B.0 C.1 D.-a
2.(2023安徽中考)下列计算正确的是( )
A.a4+a4=a8 B.a4·a4=a16
C.(a4)4=a16 D.a8÷a4=a2
3.(2021北京海淀期中)若式子(x-2)0有意义,则有理数x的取值范围是( )
A.x≠2 B.x=2 C.x≠0 D.x=0
4.【新独家原创】下列式子:①(a-3)(-a+3);②(2x+y)(2x-y);③(a+2b+c)(a-2b+c);④(-x+y)(x+y);⑤(n-m)(-m+n);⑥(a2-b)(a-b2).其中可运用平方差公式计算的有( )
A.2个 B.3个
C.4个 D.5个
5.下列计算中错误的是( )
A.4a5b3c2÷(-2a2bc)2=ab
B.(a+1)(a-1)(a2+1)=a4-1
C.4x2y·÷4x2y2=-
D.25×=x2-x+1
6.(2023北京十三中模拟)如果x2+2x-2=0,那么代数式x(x+2)+(x+1)2的值是( )
A.-5 B.5 C.3 D.-3
7.(2023北京八中期中)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台.已知广场中心有一座边长为b的正方形花坛,学生会提出两个方案:
方案一:如图1,绕花坛搭建外围是正方形的“回”字形舞台(阴影部分),面积为S1;
方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),面积为S2.
具体数据如图所示,则S1与S2的大小关系为( )
图1
图2
A.S1=S2 B.S1
8.【北京常考·动手操作题】如图,将大正方形通过剪、割、拼后分解成新的图形,利用等面积法可证明某些乘法公式,在给出的4种拼法中,能够验证平方差公式的有( )
①
②
③
④
A.①②③④ B.①②③
C.①③ D.③④
二、填空题(每小题3分,共18分)
9.(2023湖南常德中考)计算:(a2b)3= .
10.【新独家原创】计算(x2+2x+2)(x-2)-x(x2-1),并把结果按照字母x升幂排列: .
11.【新独家原创】【跨学科·物理】太阳内部高温核聚变反应释放的辐射能功率为3.8×1023千瓦,利用新型太阳能电池板可以将其中的50亿分之一转化为电能,按照一个家庭一年用电量1 000千瓦时,能满足一个中等城市760 000个家庭使用 年.
12.(2022四川德阳中考)已知(x+y)2=25,(x-y)2=9,则xy= .
13.(2021山东潍坊期末)若多项式A除以(2x2-3),得到的商式为3x-4,余式为5x+2,则A= .
14.(2022北京昌平一中期中)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
……
由此猜想(a+b)10的展开式中第三项的系数是 .
三、解答题(共58分)
15.(2023北京顺义期末)(6分)计算:
(1)(1-a)(1+a)+(a-a3)÷a;
(2)(2x2)3·x-8x4·x3.
16.(6分)用乘法公式计算:
(1)100×99;(2).
17.(2023北京平谷期末)(5分)已知x2-5x-4=0,求2x2-3(x2-2+x)-2的值.
18.(2023北京通州期中)(6分)某校有一块长为3a+b,宽为2a+b的长方形土地,计划将阴影部分进行绿化,空白正方形部分修建一座雕像,其中a>b>0.请用含a,b的代数式表示绿化部分的面积(结果化为最简形式).
19.(2022北京昌平一中期中)(7分)逆向运用幂的运算可以得到am+n=am·an,am-n=am÷an,amn=(am)n,ambm=(ab)m,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则常可化繁为简,化难为易,使问题巧妙得解.
(1)52 021×= ;
(2)若3×9m×27m=311,求m的值.
20.(8分)已知多项式A=(x+2)2+x(x-2)-(x+3)(x-3).
(1)化简多项式A时,小明的结果与其他同学的不同,请你检查小明同学的解题过程.
解:A=(x+2)2+x(x-2)-(x+3)(x-3) =x2+4+x2-x2=x2-5.
在标出①②③的三项中,出现错误的是 (填序号),请写出正确的解答过程.
(2)小亮说:“只要给出x2+2x+1的合理的值,即可求出多项式A的值.”小明给出x2+2x+1的值为4,请你求出此时A的值.
21.(2023北京东城期末)(10分)给出定义如下:我们称使等式a-b=ab+1成立的一对有理数a,b为“相伴有理数对”,记为(a,b).
(1)数对,中,是“相伴有理数对”的是 ;
(2)若(x+1,5)是“相伴有理数对”,则x的值是 ;
(3)若(a,b)是“相伴有理数对”,求3ab-a+(a+b-5ab)+1的值.
22.【数形结合思想】(2022四川成都实验学校期中)(10分)[知识生成]通常,用两种不同的方法计算同一个图形的面积可以得到一个恒等式.
例如:图1是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的方式拼成一个正方形.请解答下列问题:
(1)观察图2,请你写出(a+b)2、(a-b)2、ab之间的等量关系: .
(2)根据(1)中的等量关系解决下列问题:
若x+y=6,xy=,求(x-y)2的值.
[知识迁移]
类似地,用两种不同的方法计算同一几何体的体积也可以得到一个恒等式.
(3)根据图3,写出一个代数恒等式: .
(4)已知a+b=3,ab=1,利用(3)中的式子求的值.
图1
图2
图3
答案全解全析
1.C a·a-1=a1-1=a0=1.
2.C (a4)4=a16.故选C.
3.A ∵式子(x-2)0有意义,∴x-2≠0,解得x≠2.故选A.
4.B (2x+y)(2x-y)、(a+2b+c)(a-2b+c)和(-x+y)(x+y)中,既有符号相同的项又有符号相反的项,符合平方差公式的特点,可运用平方差公式计算.故选B.
5.D 4a5b3c2÷(-2a2bc)2=4a5b3c2÷4a4b2c2=ab,故选项A计算正确;(a+1)(a-1)(a2+1)=(a2-1)·(a2+1)=a4-1,故选项B计算正确;4x2y·÷4x2y2=-,故选项C计算正确;25×=x2-x+25,故选项D计算错误,符合题意.故选D.
6.B x(x+2)+(x+1)2=x2+2x+x2+2x+1=2x2+4x+1,
∵x2+2x-2=0,∴x2+2x=2,
∴原式=2(x2+2x)+1=2×2+1=5,
故选B.
7.C ∵题图2中由花坛和阴影组成的长方形的长是a×2+b=a+b,宽是a-b,
∴S2=(a+b)(a-b)-b2=a2-2b2,
∵S1=a2-b2,
∴S1>S2.
故选C.
8.C ①可以验证的等式为a2-b2=(a+b)(a-b),可以验证平方差公式;②可以验证的等式为a2=(a-b)2+b2+2b(a-b),不能验证平方差公式;③可以验证的等式为a2-b2=(a+b)(a-b),可以验证平方差公式;④可以验证的等式为(a+b)2=(a-b)2+4ab,不能验证平方差公式.所以能够验证平方差公式的是①③.故选C.
9.答案 a6b3
解析 (a2b)3=(a2)3b3=a6b3.
10.答案 -4-x
解析 原式=x3-2x2+2x2-4x+2x-4-x3+x=-4-x.
11.答案 100 000
解析 3.8×1023÷(5×109)÷(103)÷(7.6×105)=105=100 000.
12.答案 4
解析 ∵(x+y)2=x2+y2+2xy=25,(x-y)2=x2+y2-2xy=9,∴(x+y)2-(x-y)2=4xy=16,∴xy=4.
13.答案 6x3-8x2-4x+14
解析 ∵多项式A除以(2x2-3),得到的商式为3x-4,余式为5x+2,
∴A=(2x2-3)(3x-4)+(5x+2)=6x3-8x2-9x+12+5x+2=6x3-8x2-4x+14.
14.答案 45
解析 (a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;
(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7;
(a+b)8的展开式的系数分别为1,8,28,56,70,56,28,8,1;
(a+b)9的展开式的系数分别为1,9,36,84,126,126,84,36,9,1;
(a+b)10的展开式的系数分别为1,10,45,120,210,252,210,120,45,10,1,
则(a+b)10的展开式中第三项的系数为45.
15.解析 (1)(1-a)(1+a)+(a-a3)÷a
=1-a2+1-a2
=2-2a2.
(2)(2x2)3·x-8x4·x3
=8x6·x-8x7
=8x7-8x7
=0.
16.解析 (1)100×99=×=1002-=9 999.
(2)==202+2×20×+=413.
17.解析 ∵x2-5x-4=0,
∴x2-5x=4,
∴2x2-3(x2-2+x)-2
=2x2-3x2+6-3x-2x+2x2-1
=x2-5x+5
=4+5
=9.
18.解析 由题意得,绿化部分的面积=(3a+b)(2a+b)-(a+2b)2=6a2+3ab+2ab+b2-a2-4b2-4ab=5a2+ab-3b2.
19.解析 (1)52 021×
=
=1.
(2)∵3×9m×27m=311,
∴3×32m×33m=311,
∴31+2m+3m=311,
∴1+2m+3m=11,
解得m=2.
20.解析 (1)A=(x+2)2+x(x-2)-(x+3)(x-3)
=x2+4x+4+x2-2x-x2+9
=x2+2x+13,
故出现错误的是①③.
(2)∵x2+2x+1=4,
∴x2+2x=3,∴A=x2+2x+13=3+13=16.
21解析 (1)当a=-2,b=时,
a-b=-2-=-,
ab+1=-2×+1=,
则a-b≠ab+1,
所以不是“相伴有理数对”.
当a=-,b=-3时,
a-b=--(-3)=-+3=,
ab+1=-×(-3)+1=,
则a-b=ab+1,
所以是“相伴有理数对”.
(2)∵(x+1,5)是“相伴有理数对”,
∴x+1-5=(x+1)×5+1,
解得x=-.
(3)3ab-a+(a+b-5ab)+1
=3ab-a+a+b-ab+1
=ab-a+b+1
=ab-(a-b)+1,
∵a-b=ab+1,
∴原式=ab-(ab+1)+1
=ab-ab-+1
=.
22.解析 (1)(a+b)2-(a-b)2=4ab(答案不唯一).
(2)由(1)可知(x+y)2-(x-y)2=4xy,
∵x+y=6,xy=,
∴(x-y)2=(x+y)2-4xy=36-4×=14.
(3)(a+b)3=a3+3a2b+3ab2+b3.
(4)由(3)可知a3+b3=(a+b)3-3a2b-3ab2=(a+b)3-3ab(a+b),
把a+b=3,ab=1代入得a3+b3=33-3×1×3=18.
∴=9.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
