2024北京课改版数学七年级下册--期末素养综合测试(一)(含答案)
文档属性
| 名称 | 2024北京课改版数学七年级下册--期末素养综合测试(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 428.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北京课改版数学七年级下册
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023北京顺义期末)下列计算正确的是( )
A.a3+a4=a7 B.a3·a4=a12
C.(ab)3=a3b3 D.a6÷a3=a2
2.(2023北京延庆期末)下列采用的调查方式中,合适的是( )
A.为了解妫水河的水质情况,采用抽样调查
B.某工厂为了解所生产的产品的合格率,采用全面调查
C.某学校给学生做校服前进行尺寸大小的调查,采用抽样调查
D.为了解神舟飞船设备零件的质量情况,采用抽样调查
3.(2023北京通州期末)航天员的宇航服加入了气凝胶,可以抵御太空的高温.气凝胶是一种具有纳米多孔结构的新型材料,气凝胶颗粒尺寸通常小于0.000 000 02 m,数据0.000 000 02用科学记数法表示为( )
A.2×10-8 B.2×10-9
C.0.2×10-8 D.2×108
4.如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3的度数是( )
A.30° B.60°
C.120° D.150°
第4题图 第8题图
5.(2022北京门头沟期末)下面从左到右的变形中,因式分解正确的是( )
A.-2x2+4xy=-2x(x-2y)
B.(x+1)(x-1)=x2-1
C.x2+4x-4=(x+2)2
D.x2+16=(x+4)2
6.(2023北京海淀清华附中期末)已知关于x,y的方程组若方程组的解中x恰为整数,m也为整数,则m的值为( )
A.-1 B.1
C.-1或3 D.-1或-3
7.(2022湖南岳阳中考)某村通过直播带货对产出的稻虾米进行线上销售,连续7天的销量(单位:袋)分别为105,103,105,110,108,105,108,这组数据的众数和中位数分别是( )
A.105,108 B.105,105
C.108,105 D.108,108
8.(2022安徽芜湖期末)如图所示,由下列条件能判定AB∥CD的是( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
9.(2023浙江宁波海曙期末)若x2+2(m+1)x+9是完全平方式,则m的值是( )
A.-4或2 B.-4 C.±4 D.±2
10.若关于x的不等式组有三个整数解,关于y的方程2y+a=有正数解,则所有符合题意的整数a的和为( )
A.12 B.9 C.5 D.3
二、填空题(每小题4分,共24分)
11.(2023湖南张家界中考)因式分解:x2y+2xy+y= .
12.(2022山东济南历下期末)计算:(a2bc)2÷ab2c= .
13.(2023北京一七一中期中)某校开展“海量阅读”活动.为了解学生的课外阅读情况,随机抽取了40名学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于这40名学生一周读书时间的数据有下列说法:
①一周读书时间的中位数是9小时;
②一周读书时间的众数是8小时;
③一周读书时间的平均数是9小时;
④一周读书时间不少于9小时的人数占抽查学生的50%.
其中说法正确的序号是 .
14.(2023北京海淀师达中学月考)如图,四个等腰直角三角形拼成一个正方形,则阴影部分的面积为 .
15.(2023北京石景山模拟)如果3x2-x-1=0,那么代数式(2x+3)(2x-3)-x(x+1)的值为 .
16.(2022湖北黄石期末)已知关于x,y的二元一次方程组的解满足x+y<3,则m的取值范围是 .
三、解答题(共66分)
17.[含评分细则](6分)从单项式m4,n4,2m2n2中任选2个,并用“-”连接成一个多项式,再对其进行因式分解.
18.[含评分细则](2023北京昌平期末)(6分)先化简,再求值:(x+1)(x-3)-(-x)2+(4x2-x)÷x,其中x=.
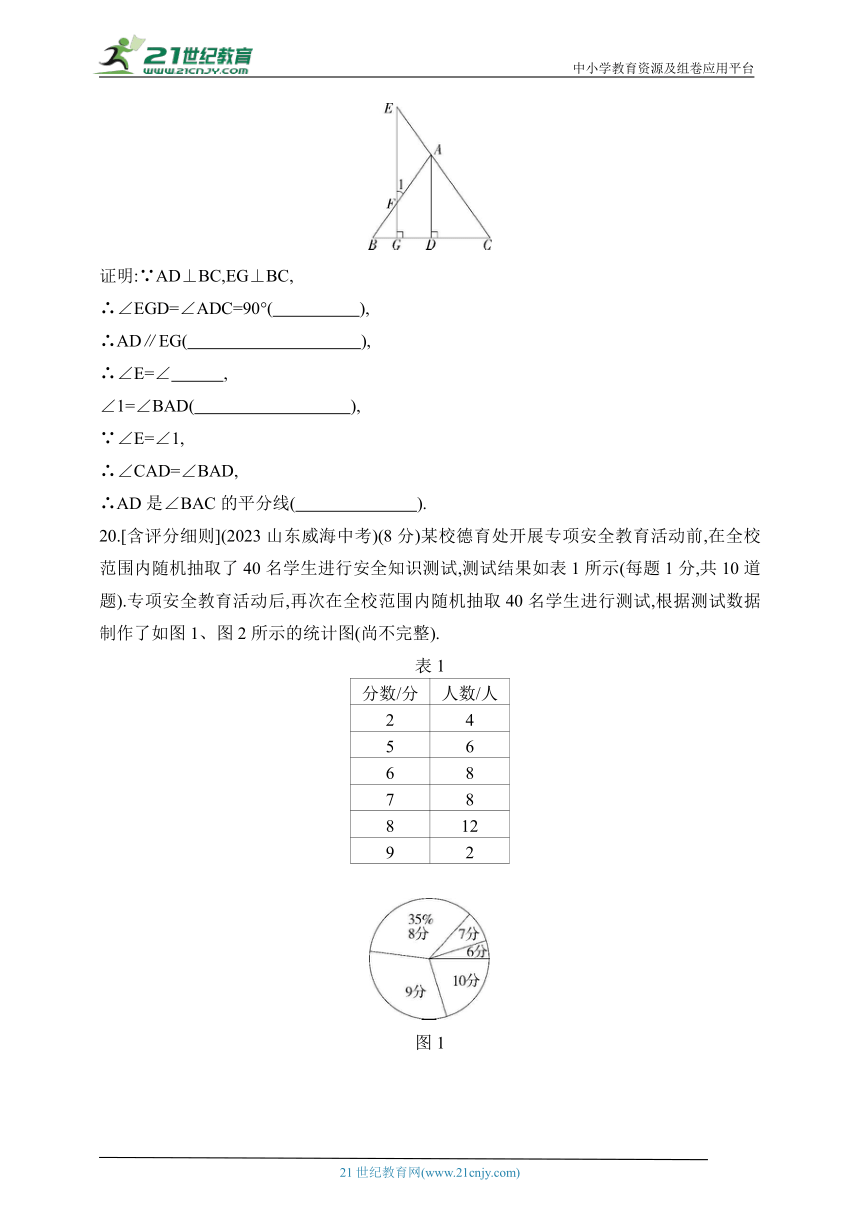
19.[含评分细则](2023北京二中期末)(8分)补全证明过程,并在( )内填写推理的依据.
已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.
求证:AD是∠BAC的平分线.
证明:∵AD⊥BC,EG⊥BC,
∴∠EGD=∠ADC=90°( ),
∴AD∥EG( ),
∴∠E=∠ ,
∠1=∠BAD( ),
∵∠E=∠1,
∴∠CAD=∠BAD,
∴AD是∠BAC的平分线( ).
20.[含评分细则](2023山东威海中考)(8分)某校德育处开展专项安全教育活动前,在全校范围内随机抽取了40名学生进行安全知识测试,测试结果如表1所示(每题1分,共10道题).专项安全教育活动后,再次在全校范围内随机抽取40名学生进行测试,根据测试数据制作了如图1、图2所示的统计图(尚不完整).
表1
分数/分 人数/人
2 4
5 6
6 8
7 8
8 12
9 2
图1
图2
设定8分及以上为合格,分析两次测试结果得到表2.
表2
平均数 /分 众数/分 中位数 /分 合格率
第一次 6.4 a 7 35%
第二次 b 8 9 c
请根据图表中的信息,解答下列问题:
(1)将图2中的统计图补充完整,并直接写出a,b,c的值;
(2)若全校学生以1 200人计算,估计专项安全教育活动后达到合格水平的学生人数;
(3)从多角度分析本次专项安全教育活动的效果.
21.[含评分细则](2022北京师大亚太实验学校期中)(8分)已知关于x,y的方程组的解中x与y的和为3,求m的值及此方程组的解.
22.[含评分细则](2023北京海淀期末)(8分)某博物馆有A,B两种不同的文创纪念品,花费400元可以购买10件A纪念品和4件B纪念品,或购买5件A纪念品和10件B纪念品.
(1)A,B两种纪念品的单价各是多少元
(2)如果想购买两种纪念品共20件,其中A纪念品不少于8件,花费最少为多少元 请说明理由.
23.[含评分细则](10分)【新考向·新定义试题】对x,y定义一种新运算F,规定:F(x,y)=(mx+ny)(3x-y)(其中m,n均为常数).例如:F(1,1)=2m+2n,F(-1,0)=3m.
已知F(1,-1)=-8,F(1,2)=13.
(1)求m,n的值;
(2)已知关于a的不等式组求a的取值范围.
24.[含评分细则](2022北京房山期末)(12分)如图,点A,B分别为∠MON的边OM,ON上的定点,点C为射线ON上的动点(不与点O,B重合).连接AC,过点C作CD⊥AC,过点B作BE∥OA,交直线CD于点F.
(1)如图1,若点C在线段OB的延长线上.
①依题意补全图1;
②用等式表示∠OAC与∠BFC的数量关系,并说明理由.
(2)如图2,若点C在线段OB上,直接用等式表示∠OAC与∠BFC的数量关系.
图1
图2
期末素养综合测试(一)
1.C a3与a4不是同类项,不能合并,故A选项计算错误;
a3·a4=a3+4=a7,所以B选项计算错误;
(ab)3=a3b3,所以C选项计算正确;
a6÷a3=a6-3=a3,所以D选项计算错误.
故选C.
2.A A.为了解妫水河的水质情况,适合采用抽样调查,因此选项A符合题意;
B.某工厂为了解所生产的产品的合格率,适合采用抽样调查,因此选项B不符合题意;
C.某学校给学生做校服前进行尺寸大小的调查,适合采用全面调查,因此选项C不符合题意;
D.为了解神舟飞船设备零件的质量情况,适合采用全面调查,因此选项D不符合题意.
故选A.
3.A 0.000 000 02=2×10-8,
故选A.
4.D ∵∠1+∠2=60°,∠1=∠2,
∴∠1=∠2=30°,
∵∠1+∠3=180°,
∴∠3=180°-∠1=180°-30°=150°.
故选D.
5.A -2x2+4xy=-2x(x-2y),故A因式分解正确,故选A.
6.D
①+②得(2+m)x=1,
解得x=,
∵x为整数,m为整数,
∴2+m=±1,
∴m的值为-1或-3.
故选D.
7.B 将这组数据按从小到大的顺序排列为103,105,105,105,108,108,110,这组数据中,出现次数最多的是105,所以众数为105.最中间的数据是105,所以中位数是105.故选B.
8.C 当∠BAC=∠DCA时,AB∥CD,故C符合题意.故选C.
9.A ∵x2+2(m+1)x+9=x2+2(m+1)x+32,
∴2(m+1)x=2x×3或2(m+1)x=-2x×3,
∴m+1=3或m+1=-3,
∴m=2或m=-4.
故选A.
10.B 不等式组整理得
∵不等式组有三个整数解,∴不等式组的解集为≤x≤,
∴整数解为-1,0,1,∴-2<≤-1,解得2方程2y+a=去分母得4y+2a=5y+6,
解得y=2a-6,∵方程有正数解,
∴2a-6>0,解得a>3.
综上,34+5=9.故选B.
11.答案 y(x+1)2
解析 x2y+2xy+y
=y(x2+2x+1)
=y(x+1)2.
12.答案 a3c
解析 原式=a4b2c2÷ab2c=a3c.
13.答案 ①②③
解析 由题表可得,这40名学生一周读书时间的中位数是(9+9)÷2=9(小时),故①中说法正确;
8小时出现的次数最多,所以众数是8小时,故②中说法正确;
这40名学生一周读书时间的平均数是×(7×6+8×10+9×9+10×8+11×7)=9(小时),故③中说法正确;
一周读书时间不少于9小时的人数占抽查学生的百分比为×100%=60%,故④中说法错误.
故答案为①②③.
14.答案 2ab
解析 阴影部分的面积为(a+b)2-2×b2-2×a2
=a2+2ab+b2-b2-a2=2ab.
15.答案 -8
解析 ∵3x2-x-1=0,
∴3x2-x=1,
∴(2x+3)(2x-3)-x(x+1)
=4x2-9-x2-x
=3x2-x-9
=1-9
=-8.
16.答案 m>-
解析
①-②得2x+2y=-4m-4,即x+y=-2m-2,
∵x+y<3,∴-2m-2<3,解得m>-.
17. 解析 m4-n4=(m2+n2)(m2-n2)3分
=(m2+n2)(m-n)(m+n).答案不唯一.6分
18. 解析 (x+1)(x-3)-(-x)2+(4x2-x)÷x
=x2-2x-3-x2+4x-13分
=2x-4,4分
当x=时,原式=2×-4=-3.6分
19. 解析 ∵AD⊥BC,EG⊥BC,
∴∠EGD=∠ADC=90°(垂直的定义),1分
∴AD∥EG(同位角相等,两直线平行),3分
∴∠E=∠CAD,5分
∠1=∠BAD(两直线平行,内错角相等),7分
∵∠E=∠1,
∴∠CAD=∠BAD,
∴AD是∠BAC的平分线(角平分线的定义).8分
20. 解析 (1)第二次抽取的40名学生中,8分的人数为40×35%=14,
故7分的人数为40-2-8-13-14=3.1分
补全统计图如下:
a=8,2分
b=×(2×6+3×7+14×8+13×9+8×10)=8.55,3分
c=×100%=87.5%.4分
(2)1 200×87.5%=1 050(人).
答:估计专项安全教育活动后达到合格水平的学生人数为1 050.6分
(3)专项安全教育活动的效果良好,理由如下:
专项安全教育活动后,学生测试成绩的平均数、中位数以及合格率均比专项安全教育活动前高,所以专项安全教育活动的效果良好.8分
21. 解析 解得3分
∴x+y=,
∵x与y的和为3,∴=3,
解得m=5.5分
把m=5代入
解得7分
∴m的值为5,方程组的解为8分
22. 解析 (1)设A纪念品的单价是x元,B纪念品的单价是y元,
根据题意得3分
解得
答:A纪念品的单价是30元,B纪念品的单价是25元.4分
(2)花费最少为540元.5分
理由:∵30>25,
∴A纪念品的单价高于B纪念品的单价,6分
∴当购买A纪念品越少时,花费越少,7分
∴当购买8件A纪念品时,花费最少,花费最少为30×8+25×(20-8)=540(元).
答:花费最少为540元.8分
23. 解析 (1)根据题意得F(1,-1)=(m-n)(3×1+1)=-8,即m-n=-2①,
F(1,2)=(m+2n)(3×1-2)=13,即m+2n=13②,
由①②得m=3,n=5.4分
(2)由(1)得F(x,y)=(3x+5y)(3x-y),
则F(a,3a+1)=(3a+15a+5)(3a-3a-1)=-18a-5,
F(5a,2-3a)=(15a+10-15a)(15a-2+3a)=180a-20.6分
由题意得8分
解不等式①得a<5,
解不等式②得a≥2,
故原不等式组的解集为2≤a<5.10分
24. 解析 (1)①补全图形如下:
3分
②∠OAC+∠BFC=90°.5分
理由:如图,设BE交AC于G,
∵CD⊥AC,∴∠FCG=90°,
∴∠FGC+∠BFC=90°,
∵OA∥BE,∴∠OAC=∠FGC,
∴∠OAC+∠BFC=90°.7分
(2)∠BFC=90°+∠OAC.12分
详解:延长AC交直线BE于H,如图.
∵BE∥OA,
∴∠OAC=∠CHF,
∵CD⊥AC,
∴∠FCH=90°,
∵∠BFC=180°-∠HFC=∠FCH+∠CHF,
∴∠BFC=90°+∠OAC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北京课改版数学七年级下册
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023北京顺义期末)下列计算正确的是( )
A.a3+a4=a7 B.a3·a4=a12
C.(ab)3=a3b3 D.a6÷a3=a2
2.(2023北京延庆期末)下列采用的调查方式中,合适的是( )
A.为了解妫水河的水质情况,采用抽样调查
B.某工厂为了解所生产的产品的合格率,采用全面调查
C.某学校给学生做校服前进行尺寸大小的调查,采用抽样调查
D.为了解神舟飞船设备零件的质量情况,采用抽样调查
3.(2023北京通州期末)航天员的宇航服加入了气凝胶,可以抵御太空的高温.气凝胶是一种具有纳米多孔结构的新型材料,气凝胶颗粒尺寸通常小于0.000 000 02 m,数据0.000 000 02用科学记数法表示为( )
A.2×10-8 B.2×10-9
C.0.2×10-8 D.2×108
4.如图,直线a,b相交于点O,如果∠1+∠2=60°,那么∠3的度数是( )
A.30° B.60°
C.120° D.150°
第4题图 第8题图
5.(2022北京门头沟期末)下面从左到右的变形中,因式分解正确的是( )
A.-2x2+4xy=-2x(x-2y)
B.(x+1)(x-1)=x2-1
C.x2+4x-4=(x+2)2
D.x2+16=(x+4)2
6.(2023北京海淀清华附中期末)已知关于x,y的方程组若方程组的解中x恰为整数,m也为整数,则m的值为( )
A.-1 B.1
C.-1或3 D.-1或-3
7.(2022湖南岳阳中考)某村通过直播带货对产出的稻虾米进行线上销售,连续7天的销量(单位:袋)分别为105,103,105,110,108,105,108,这组数据的众数和中位数分别是( )
A.105,108 B.105,105
C.108,105 D.108,108
8.(2022安徽芜湖期末)如图所示,由下列条件能判定AB∥CD的是( )
A.∠BAC=∠DAC B.∠DAC=∠ACB
C.∠BAC=∠DCA D.∠D+∠DCB=180°
9.(2023浙江宁波海曙期末)若x2+2(m+1)x+9是完全平方式,则m的值是( )
A.-4或2 B.-4 C.±4 D.±2
10.若关于x的不等式组有三个整数解,关于y的方程2y+a=有正数解,则所有符合题意的整数a的和为( )
A.12 B.9 C.5 D.3
二、填空题(每小题4分,共24分)
11.(2023湖南张家界中考)因式分解:x2y+2xy+y= .
12.(2022山东济南历下期末)计算:(a2bc)2÷ab2c= .
13.(2023北京一七一中期中)某校开展“海量阅读”活动.为了解学生的课外阅读情况,随机抽取了40名学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于这40名学生一周读书时间的数据有下列说法:
①一周读书时间的中位数是9小时;
②一周读书时间的众数是8小时;
③一周读书时间的平均数是9小时;
④一周读书时间不少于9小时的人数占抽查学生的50%.
其中说法正确的序号是 .
14.(2023北京海淀师达中学月考)如图,四个等腰直角三角形拼成一个正方形,则阴影部分的面积为 .
15.(2023北京石景山模拟)如果3x2-x-1=0,那么代数式(2x+3)(2x-3)-x(x+1)的值为 .
16.(2022湖北黄石期末)已知关于x,y的二元一次方程组的解满足x+y<3,则m的取值范围是 .
三、解答题(共66分)
17.[含评分细则](6分)从单项式m4,n4,2m2n2中任选2个,并用“-”连接成一个多项式,再对其进行因式分解.
18.[含评分细则](2023北京昌平期末)(6分)先化简,再求值:(x+1)(x-3)-(-x)2+(4x2-x)÷x,其中x=.
19.[含评分细则](2023北京二中期末)(8分)补全证明过程,并在( )内填写推理的依据.
已知:如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.
求证:AD是∠BAC的平分线.
证明:∵AD⊥BC,EG⊥BC,
∴∠EGD=∠ADC=90°( ),
∴AD∥EG( ),
∴∠E=∠ ,
∠1=∠BAD( ),
∵∠E=∠1,
∴∠CAD=∠BAD,
∴AD是∠BAC的平分线( ).
20.[含评分细则](2023山东威海中考)(8分)某校德育处开展专项安全教育活动前,在全校范围内随机抽取了40名学生进行安全知识测试,测试结果如表1所示(每题1分,共10道题).专项安全教育活动后,再次在全校范围内随机抽取40名学生进行测试,根据测试数据制作了如图1、图2所示的统计图(尚不完整).
表1
分数/分 人数/人
2 4
5 6
6 8
7 8
8 12
9 2
图1
图2
设定8分及以上为合格,分析两次测试结果得到表2.
表2
平均数 /分 众数/分 中位数 /分 合格率
第一次 6.4 a 7 35%
第二次 b 8 9 c
请根据图表中的信息,解答下列问题:
(1)将图2中的统计图补充完整,并直接写出a,b,c的值;
(2)若全校学生以1 200人计算,估计专项安全教育活动后达到合格水平的学生人数;
(3)从多角度分析本次专项安全教育活动的效果.
21.[含评分细则](2022北京师大亚太实验学校期中)(8分)已知关于x,y的方程组的解中x与y的和为3,求m的值及此方程组的解.
22.[含评分细则](2023北京海淀期末)(8分)某博物馆有A,B两种不同的文创纪念品,花费400元可以购买10件A纪念品和4件B纪念品,或购买5件A纪念品和10件B纪念品.
(1)A,B两种纪念品的单价各是多少元
(2)如果想购买两种纪念品共20件,其中A纪念品不少于8件,花费最少为多少元 请说明理由.
23.[含评分细则](10分)【新考向·新定义试题】对x,y定义一种新运算F,规定:F(x,y)=(mx+ny)(3x-y)(其中m,n均为常数).例如:F(1,1)=2m+2n,F(-1,0)=3m.
已知F(1,-1)=-8,F(1,2)=13.
(1)求m,n的值;
(2)已知关于a的不等式组求a的取值范围.
24.[含评分细则](2022北京房山期末)(12分)如图,点A,B分别为∠MON的边OM,ON上的定点,点C为射线ON上的动点(不与点O,B重合).连接AC,过点C作CD⊥AC,过点B作BE∥OA,交直线CD于点F.
(1)如图1,若点C在线段OB的延长线上.
①依题意补全图1;
②用等式表示∠OAC与∠BFC的数量关系,并说明理由.
(2)如图2,若点C在线段OB上,直接用等式表示∠OAC与∠BFC的数量关系.
图1
图2
期末素养综合测试(一)
1.C a3与a4不是同类项,不能合并,故A选项计算错误;
a3·a4=a3+4=a7,所以B选项计算错误;
(ab)3=a3b3,所以C选项计算正确;
a6÷a3=a6-3=a3,所以D选项计算错误.
故选C.
2.A A.为了解妫水河的水质情况,适合采用抽样调查,因此选项A符合题意;
B.某工厂为了解所生产的产品的合格率,适合采用抽样调查,因此选项B不符合题意;
C.某学校给学生做校服前进行尺寸大小的调查,适合采用全面调查,因此选项C不符合题意;
D.为了解神舟飞船设备零件的质量情况,适合采用全面调查,因此选项D不符合题意.
故选A.
3.A 0.000 000 02=2×10-8,
故选A.
4.D ∵∠1+∠2=60°,∠1=∠2,
∴∠1=∠2=30°,
∵∠1+∠3=180°,
∴∠3=180°-∠1=180°-30°=150°.
故选D.
5.A -2x2+4xy=-2x(x-2y),故A因式分解正确,故选A.
6.D
①+②得(2+m)x=1,
解得x=,
∵x为整数,m为整数,
∴2+m=±1,
∴m的值为-1或-3.
故选D.
7.B 将这组数据按从小到大的顺序排列为103,105,105,105,108,108,110,这组数据中,出现次数最多的是105,所以众数为105.最中间的数据是105,所以中位数是105.故选B.
8.C 当∠BAC=∠DCA时,AB∥CD,故C符合题意.故选C.
9.A ∵x2+2(m+1)x+9=x2+2(m+1)x+32,
∴2(m+1)x=2x×3或2(m+1)x=-2x×3,
∴m+1=3或m+1=-3,
∴m=2或m=-4.
故选A.
10.B 不等式组整理得
∵不等式组有三个整数解,∴不等式组的解集为≤x≤,
∴整数解为-1,0,1,∴-2<≤-1,解得2
解得y=2a-6,∵方程有正数解,
∴2a-6>0,解得a>3.
综上,3
11.答案 y(x+1)2
解析 x2y+2xy+y
=y(x2+2x+1)
=y(x+1)2.
12.答案 a3c
解析 原式=a4b2c2÷ab2c=a3c.
13.答案 ①②③
解析 由题表可得,这40名学生一周读书时间的中位数是(9+9)÷2=9(小时),故①中说法正确;
8小时出现的次数最多,所以众数是8小时,故②中说法正确;
这40名学生一周读书时间的平均数是×(7×6+8×10+9×9+10×8+11×7)=9(小时),故③中说法正确;
一周读书时间不少于9小时的人数占抽查学生的百分比为×100%=60%,故④中说法错误.
故答案为①②③.
14.答案 2ab
解析 阴影部分的面积为(a+b)2-2×b2-2×a2
=a2+2ab+b2-b2-a2=2ab.
15.答案 -8
解析 ∵3x2-x-1=0,
∴3x2-x=1,
∴(2x+3)(2x-3)-x(x+1)
=4x2-9-x2-x
=3x2-x-9
=1-9
=-8.
16.答案 m>-
解析
①-②得2x+2y=-4m-4,即x+y=-2m-2,
∵x+y<3,∴-2m-2<3,解得m>-.
17. 解析 m4-n4=(m2+n2)(m2-n2)3分
=(m2+n2)(m-n)(m+n).答案不唯一.6分
18. 解析 (x+1)(x-3)-(-x)2+(4x2-x)÷x
=x2-2x-3-x2+4x-13分
=2x-4,4分
当x=时,原式=2×-4=-3.6分
19. 解析 ∵AD⊥BC,EG⊥BC,
∴∠EGD=∠ADC=90°(垂直的定义),1分
∴AD∥EG(同位角相等,两直线平行),3分
∴∠E=∠CAD,5分
∠1=∠BAD(两直线平行,内错角相等),7分
∵∠E=∠1,
∴∠CAD=∠BAD,
∴AD是∠BAC的平分线(角平分线的定义).8分
20. 解析 (1)第二次抽取的40名学生中,8分的人数为40×35%=14,
故7分的人数为40-2-8-13-14=3.1分
补全统计图如下:
a=8,2分
b=×(2×6+3×7+14×8+13×9+8×10)=8.55,3分
c=×100%=87.5%.4分
(2)1 200×87.5%=1 050(人).
答:估计专项安全教育活动后达到合格水平的学生人数为1 050.6分
(3)专项安全教育活动的效果良好,理由如下:
专项安全教育活动后,学生测试成绩的平均数、中位数以及合格率均比专项安全教育活动前高,所以专项安全教育活动的效果良好.8分
21. 解析 解得3分
∴x+y=,
∵x与y的和为3,∴=3,
解得m=5.5分
把m=5代入
解得7分
∴m的值为5,方程组的解为8分
22. 解析 (1)设A纪念品的单价是x元,B纪念品的单价是y元,
根据题意得3分
解得
答:A纪念品的单价是30元,B纪念品的单价是25元.4分
(2)花费最少为540元.5分
理由:∵30>25,
∴A纪念品的单价高于B纪念品的单价,6分
∴当购买A纪念品越少时,花费越少,7分
∴当购买8件A纪念品时,花费最少,花费最少为30×8+25×(20-8)=540(元).
答:花费最少为540元.8分
23. 解析 (1)根据题意得F(1,-1)=(m-n)(3×1+1)=-8,即m-n=-2①,
F(1,2)=(m+2n)(3×1-2)=13,即m+2n=13②,
由①②得m=3,n=5.4分
(2)由(1)得F(x,y)=(3x+5y)(3x-y),
则F(a,3a+1)=(3a+15a+5)(3a-3a-1)=-18a-5,
F(5a,2-3a)=(15a+10-15a)(15a-2+3a)=180a-20.6分
由题意得8分
解不等式①得a<5,
解不等式②得a≥2,
故原不等式组的解集为2≤a<5.10分
24. 解析 (1)①补全图形如下:
3分
②∠OAC+∠BFC=90°.5分
理由:如图,设BE交AC于G,
∵CD⊥AC,∴∠FCG=90°,
∴∠FGC+∠BFC=90°,
∵OA∥BE,∴∠OAC=∠FGC,
∴∠OAC+∠BFC=90°.7分
(2)∠BFC=90°+∠OAC.12分
详解:延长AC交直线BE于H,如图.
∵BE∥OA,
∴∠OAC=∠CHF,
∵CD⊥AC,
∴∠FCH=90°,
∵∠BFC=180°-∠HFC=∠FCH+∠CHF,
∴∠BFC=90°+∠OAC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
