2024北京课改版数学七年级下册--专项素养综合全练(九)以平行线为载体的探索类问题(含解析)
文档属性
| 名称 | 2024北京课改版数学七年级下册--专项素养综合全练(九)以平行线为载体的探索类问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 351.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北京课改版数学七年级下册
专项素养综合全练(九)
以平行线为载体的探索类问题
类型一 “拐点”问题
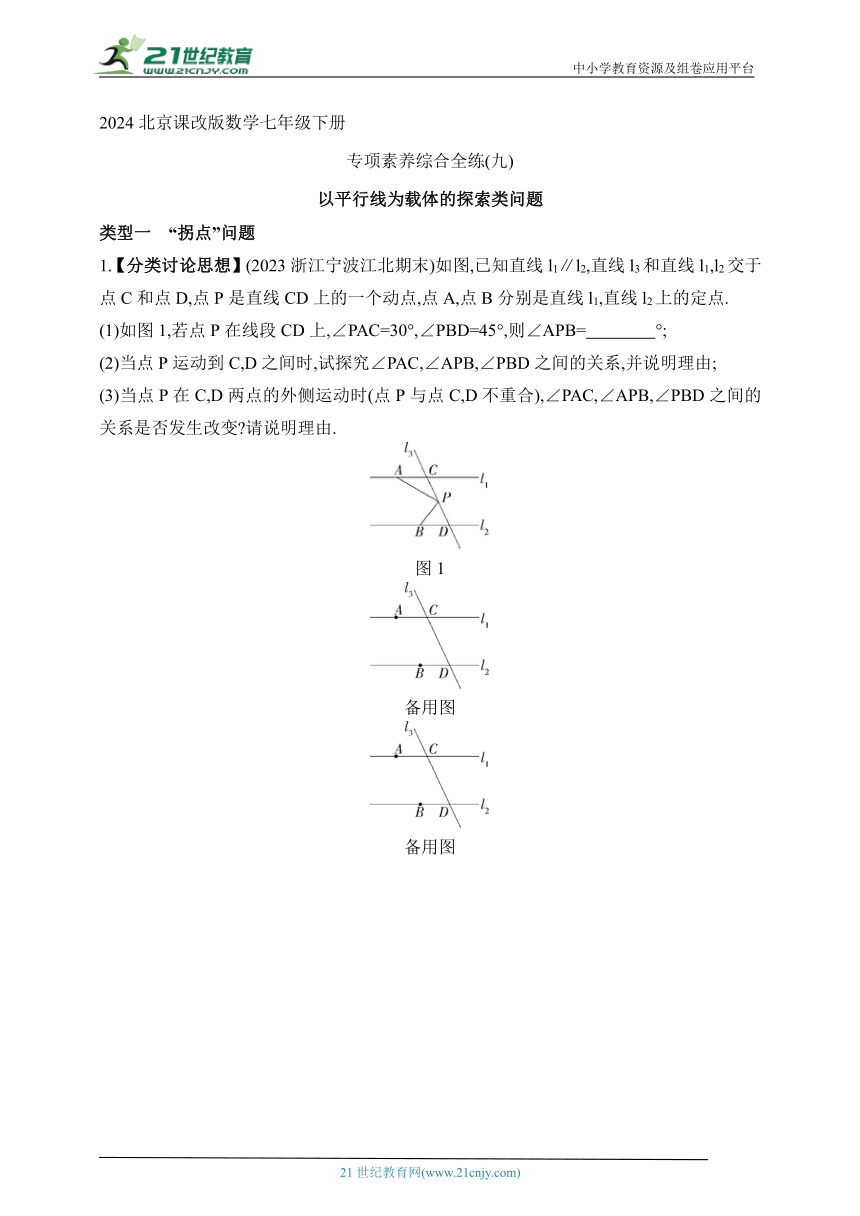
1.【分类讨论思想】(2023浙江宁波江北期末)如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和点D,点P是直线CD上的一个动点,点A,点B分别是直线l1,直线l2上的定点.
(1)如图1,若点P在线段CD上,∠PAC=30°,∠PBD=45°,则∠APB= °;
(2)当点P运动到C,D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由;
(3)当点P在C,D两点的外侧运动时(点P与点C,D不重合),∠PAC,∠APB,∠PBD之间的关系是否发生改变 请说明理由.
图1
备用图
备用图
类型二 “动点(图)”问题
2.(2023北京二中期中)如图,点P为直线AB外一点,过点P作直线CD∥AB.现将一个含30°角的三角板EFG按如图1所示的方式放置,使点F、E分别在直线AB、CD上,且点E在点P的右侧,∠G=90°,∠EFG=30°,设∠GFB=α(0°<α<90°).
(1)填空:∠DEG+∠BFG= °.
(2)若∠CEF的平分线EH交直线AB于点H,如图2.
①当EH∥FG时,求α的值.
②在①的条件下,将三角板EFG绕点E以每秒1°的转速进行顺时针旋转,同时射线PC绕点P以每秒4°的转速进行顺时针旋转,射线PC旋转一周后停止转动,同时三角板EFG也停止转动,设转动时间为t秒.在旋转过程中,当t= 时,CP∥EG.
图1
图2
备用图
答案全解全析
1.解析 (1)75.
(2)∠APB=∠PAC+∠PBD,
理由:如图1,过点P作PE∥l1,
图1
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD.
(3)发生改变.
如图2,当点P在CD延长线上时,∠PAC=∠APB+∠PBD.
图2
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE-∠BPE=∠PAC-∠PBD,
∴∠PAC=∠APB+∠PBD.
如图3,当点P在DC延长线上时,∠PBD=∠PAC+∠APB.
图3
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠BPE-∠APE=∠PBD-∠PAC,
∴∠PBD=∠PAC+∠APB.
综上所述,点P在C,D两点的外侧运动时(点P与点C,D不重合),∠PAC,∠APB,∠PBD之间的关系发生改变.
方法归纳 利用平行线的判定与性质求角度是常考题型,但通常会遇到有平行线却找不到相应的“截线”,导致平行线的判定与性质在解题中无法直接运用的题型,此时需要添加辅助线,构造出“三线八角”,常见模型有“铅笔”模型、“猪蹄”模型、“脚丫”模型、“弯折”模型等.
2.解析 (1)90.详解:过点G作AB的平行线GM,如图:
∵CD∥AB,MG∥AB,
∴CD∥MG,∠MGF=∠GFB,
∴∠DEG=∠EGM,
∴∠DEG+∠BFG=∠EGM+∠MGF=∠EGF=90°,
即∠DEG+∠BFG=90°.
(2)①∵EH∥FG,
∴∠GFB=∠EHF=α,
∵EH平分∠CEF,
∴∠CEH=∠FEH=α,
又∵CD∥AB,
∴∠CEF=∠EFB,
∴2α=30°+α,
解得α=30°.
②20或80.
详解:易知0≤t≤90,分情况讨论:
当0≤t≤45时,如图:
当射线PC旋转到PC'时,△EGF旋转至△EG'F',延长G'E至点H,
∵PC'∥G'H,
∴∠CPC'=∠CEH,
∵∠CEH=∠DEG',
∴∠CPC'=∠DEG',
由题意得,∠CPC'=(4t)°,∠DEG'=(60+t)°,
∴4t=60+t,
解得t=20.
当45∵CP∥EG,
∴∠DPC=∠DEG,
∴4t-180=60+t,得t=80.
故t=20或80.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北京课改版数学七年级下册
专项素养综合全练(九)
以平行线为载体的探索类问题
类型一 “拐点”问题
1.【分类讨论思想】(2023浙江宁波江北期末)如图,已知直线l1∥l2,直线l3和直线l1,l2交于点C和点D,点P是直线CD上的一个动点,点A,点B分别是直线l1,直线l2上的定点.
(1)如图1,若点P在线段CD上,∠PAC=30°,∠PBD=45°,则∠APB= °;
(2)当点P运动到C,D之间时,试探究∠PAC,∠APB,∠PBD之间的关系,并说明理由;
(3)当点P在C,D两点的外侧运动时(点P与点C,D不重合),∠PAC,∠APB,∠PBD之间的关系是否发生改变 请说明理由.
图1
备用图
备用图
类型二 “动点(图)”问题
2.(2023北京二中期中)如图,点P为直线AB外一点,过点P作直线CD∥AB.现将一个含30°角的三角板EFG按如图1所示的方式放置,使点F、E分别在直线AB、CD上,且点E在点P的右侧,∠G=90°,∠EFG=30°,设∠GFB=α(0°<α<90°).
(1)填空:∠DEG+∠BFG= °.
(2)若∠CEF的平分线EH交直线AB于点H,如图2.
①当EH∥FG时,求α的值.
②在①的条件下,将三角板EFG绕点E以每秒1°的转速进行顺时针旋转,同时射线PC绕点P以每秒4°的转速进行顺时针旋转,射线PC旋转一周后停止转动,同时三角板EFG也停止转动,设转动时间为t秒.在旋转过程中,当t= 时,CP∥EG.
图1
图2
备用图
答案全解全析
1.解析 (1)75.
(2)∠APB=∠PAC+∠PBD,
理由:如图1,过点P作PE∥l1,
图1
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∴∠APE+∠BPE=∠PAC+∠PBD,
∴∠APB=∠PAC+∠PBD.
(3)发生改变.
如图2,当点P在CD延长线上时,∠PAC=∠APB+∠PBD.
图2
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠APE-∠BPE=∠PAC-∠PBD,
∴∠PAC=∠APB+∠PBD.
如图3,当点P在DC延长线上时,∠PBD=∠PAC+∠APB.
图3
理由:过点P作PE∥l1,
∴∠APE=∠PAC,
∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APB=∠BPE-∠APE=∠PBD-∠PAC,
∴∠PBD=∠PAC+∠APB.
综上所述,点P在C,D两点的外侧运动时(点P与点C,D不重合),∠PAC,∠APB,∠PBD之间的关系发生改变.
方法归纳 利用平行线的判定与性质求角度是常考题型,但通常会遇到有平行线却找不到相应的“截线”,导致平行线的判定与性质在解题中无法直接运用的题型,此时需要添加辅助线,构造出“三线八角”,常见模型有“铅笔”模型、“猪蹄”模型、“脚丫”模型、“弯折”模型等.
2.解析 (1)90.详解:过点G作AB的平行线GM,如图:
∵CD∥AB,MG∥AB,
∴CD∥MG,∠MGF=∠GFB,
∴∠DEG=∠EGM,
∴∠DEG+∠BFG=∠EGM+∠MGF=∠EGF=90°,
即∠DEG+∠BFG=90°.
(2)①∵EH∥FG,
∴∠GFB=∠EHF=α,
∵EH平分∠CEF,
∴∠CEH=∠FEH=α,
又∵CD∥AB,
∴∠CEF=∠EFB,
∴2α=30°+α,
解得α=30°.
②20或80.
详解:易知0≤t≤90,分情况讨论:
当0≤t≤45时,如图:
当射线PC旋转到PC'时,△EGF旋转至△EG'F',延长G'E至点H,
∵PC'∥G'H,
∴∠CPC'=∠CEH,
∵∠CEH=∠DEG',
∴∠CPC'=∠DEG',
由题意得,∠CPC'=(4t)°,∠DEG'=(60+t)°,
∴4t=60+t,
解得t=20.
当45
∴∠DPC=∠DEG,
∴4t-180=60+t,得t=80.
故t=20或80.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
