2.2.2去括号、添括号 课件(共18张PPT) 2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 2.2.2去括号、添括号 课件(共18张PPT) 2023—2024学年沪科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:16:18 | ||
图片预览





文档简介
(共18张PPT)
第二章 整式加减
2.2 整式加减
2.2.2 去括号、添括号
1.掌握去括号法则,知道去括号法则也是将整式化简的一种方法
2.能逆用去括号法则,并掌握添括号法则
一、学习目标
二、新课导入
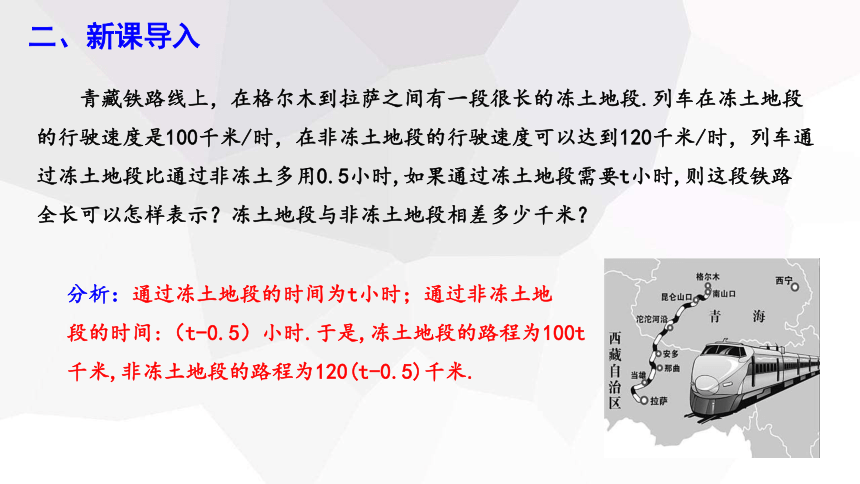
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段
的行驶速度是100千米/时,在非冻土地段的行驶速度可以达到120千米/时,列车通
过冻土地段比通过非冻土多用0.5小时,如果通过冻土地段需要t小时,则这段铁路
全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
分析:通过冻土地段的时间为t小时;通过非冻土地
段的时间:(t-0.5)小时.于是,冻土地段的路程为100t
千米,非冻土地段的路程为120(t-0.5)千米.
二、新课导入
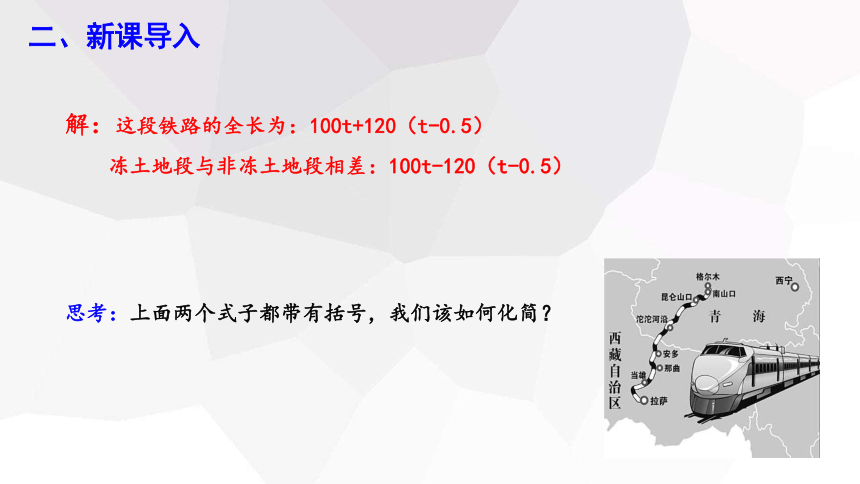
解:这段铁路的全长为:100t+120(t-0.5)
冻土地段与非冻土地段相差:100t-120(t-0.5)
思考:上面两个式子都带有括号,我们该如何化简?
三、概念剖析
化简
100t+120(t-0.5)
100t-120(t-0.5)
类比数的运算,我们可以利用分配律,去括号,再合并同类项,得
100t+120(t-0.5)=100t+120t-60=220t-60
100t-120(t-0.5)=100t-120t+60=-20t+60
上面两式中:+120(t-0.5)=+120t-60;-120(t-0.5)=-120t+60
通过比较这两个式子,你能发现去括号时符号变化的规律吗
三、概念剖析
去括号法则
1.如果括号前面是“+”号,去括号时把括号连同它前面的“+”号去掉,括号内的各项都不改变符号;
2.如果括号前面是“-”号时,去括号时把括号连同它前面的“-”号去掉,括号内的各项都改变符号.
三、概念剖析
观察下列各式:
①-a+b=-(a-b); ②2-3x=-(3x-2); ③5x+30=5(x+6)
思考:它和去括号法则有什么不同?
添括号法则:
(1)所添括号前面是“+”号,括到括号里的各项都不改变符号;
(2)所添括号前面是“-”号,括到括号里的各项都改变符号.
四、典型例题
例1.去括号:
(1)2(x2-3x) =
(2)-4(x2-1)=
2x2-6x;
-4x2 +4;
(3)-2n(5m-n)=
-10mn+2n ;
(4)3(p2-2q)=
3p2-6q;
总结:括号前面因数是正数时,括号内的每一项符号不变;括号前面因数是负数时,括号内的每一项都要改变符号.
【当堂检测】
1.下列各项去括号正确的是( )
A.-4(m+n)-mn=-4m+4n-mn
B.-(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2
C.ab-6(-a+4)=ab-6a+4
D.x2-3(3x-y+3)=x2-9x-3y+5
B
【当堂检测】
2.去括号:
(1)8b+ (-4a-3); (2)-(-3y+6b);
(3)3-(4x-2y); (4)-6x+(a-b)
解:原式=8b-4a-3
解:原式=3y-6b
解:原式=3-4x+2y
解:原式=-6x+a-b
四、典型例题
例2.按下列要求给多项式-a5+3a3-a2+2添括号.
(1)使最高次项系数变为正数;
(2)使二次项系数变为正数;
(3)把奇次项放在前面是“-”号的括号里,其余的项放在前面是“+”号的括号里.
解:(1)根据题意可得:-(a5-3a3+a2-1);
(2)根据题意可得:-(a5-3a3+a2+2);
(3)根据题意可得:-(a5-3a3)+(-a2+2).
四、典型例题
总结:
在给式子添括号时,括号前的正负号改变,括号内的各项同时变号.
【当堂检测】
3.下列式子中,正确的是( )
A.5x2-3x+7y=5x2-(3x+7y)
B.3x2-3x+7y=3x2-(7y-3x)
C.3x2-4x+2y2 = 3x2-(4x-2y2)
D.5x2-6x-y2 = 5x2-(6x-y2)
C
【当堂检测】
4.把-3x2-4xy+2y2-4x+y+2中的二次项放在前面带有“-”号的括号里,一次项放在前面带有“+”号的括号里.
解:-3x2-4xy+2y2-4x+y+2
=-(3x2+4xy-2y2)+(-4x+y)+2.
四、典型例题
例3.先去括号,再合并同类项.
(1)3a+3(a+1)-4(a-2); (2)4a2-3a+3-3(-a3+2a+1).
解:原式=3a+3a+3-4a+8
=(3a+3a-4a)+(3+8)
= 2a+11;
原式=4a2-3a+3+3a3-6a-3
=4a2+(-3a-6a)+(3-3)+3a3
= 4a2-9a+3a3.
注意:(1)括号前是负号,去括号时不能忘记变号;
(2)括号前有数字,不能漏乘括号前的数字.
【当堂检测】
5.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )
A.1 B.5 C.-5 D.-1
B
【当堂检测】
6.去括号,合并同类项.
(1) (2)-4(3x2-2xy)+5(x2+2xy-7)
解:原式=
=
=
原式=-12x2+8xy+5x2+10xy-35
=(-12x2+5x2)+(8xy+10xy)-35
= -7x2+18xy-35
五、课堂总结
1.去括号法则:
(1)如果括号前面是“+”号,去括号时把括号连同它前面的“+”号去掉,括号内的各项都不改变符号;
(2)如果括号前面是“-”号时,去括号时把括号连同它前面的“-”号去掉,括号内的各项都改变符号.
2.添括号法则:
(1)所添括号前面是“+”号,括到括号里的各项都不改变符号;
(2)所添括号前面是“-”号,括到括号里的各项都改变符号.
第二章 整式加减
2.2 整式加减
2.2.2 去括号、添括号
1.掌握去括号法则,知道去括号法则也是将整式化简的一种方法
2.能逆用去括号法则,并掌握添括号法则
一、学习目标
二、新课导入
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段
的行驶速度是100千米/时,在非冻土地段的行驶速度可以达到120千米/时,列车通
过冻土地段比通过非冻土多用0.5小时,如果通过冻土地段需要t小时,则这段铁路
全长可以怎样表示?冻土地段与非冻土地段相差多少千米?
分析:通过冻土地段的时间为t小时;通过非冻土地
段的时间:(t-0.5)小时.于是,冻土地段的路程为100t
千米,非冻土地段的路程为120(t-0.5)千米.
二、新课导入
解:这段铁路的全长为:100t+120(t-0.5)
冻土地段与非冻土地段相差:100t-120(t-0.5)
思考:上面两个式子都带有括号,我们该如何化简?
三、概念剖析
化简
100t+120(t-0.5)
100t-120(t-0.5)
类比数的运算,我们可以利用分配律,去括号,再合并同类项,得
100t+120(t-0.5)=100t+120t-60=220t-60
100t-120(t-0.5)=100t-120t+60=-20t+60
上面两式中:+120(t-0.5)=+120t-60;-120(t-0.5)=-120t+60
通过比较这两个式子,你能发现去括号时符号变化的规律吗
三、概念剖析
去括号法则
1.如果括号前面是“+”号,去括号时把括号连同它前面的“+”号去掉,括号内的各项都不改变符号;
2.如果括号前面是“-”号时,去括号时把括号连同它前面的“-”号去掉,括号内的各项都改变符号.
三、概念剖析
观察下列各式:
①-a+b=-(a-b); ②2-3x=-(3x-2); ③5x+30=5(x+6)
思考:它和去括号法则有什么不同?
添括号法则:
(1)所添括号前面是“+”号,括到括号里的各项都不改变符号;
(2)所添括号前面是“-”号,括到括号里的各项都改变符号.
四、典型例题
例1.去括号:
(1)2(x2-3x) =
(2)-4(x2-1)=
2x2-6x;
-4x2 +4;
(3)-2n(5m-n)=
-10mn+2n ;
(4)3(p2-2q)=
3p2-6q;
总结:括号前面因数是正数时,括号内的每一项符号不变;括号前面因数是负数时,括号内的每一项都要改变符号.
【当堂检测】
1.下列各项去括号正确的是( )
A.-4(m+n)-mn=-4m+4n-mn
B.-(5x-3y)+4(2xy-y2)=-5x+3y+8xy-4y2
C.ab-6(-a+4)=ab-6a+4
D.x2-3(3x-y+3)=x2-9x-3y+5
B
【当堂检测】
2.去括号:
(1)8b+ (-4a-3); (2)-(-3y+6b);
(3)3-(4x-2y); (4)-6x+(a-b)
解:原式=8b-4a-3
解:原式=3y-6b
解:原式=3-4x+2y
解:原式=-6x+a-b
四、典型例题
例2.按下列要求给多项式-a5+3a3-a2+2添括号.
(1)使最高次项系数变为正数;
(2)使二次项系数变为正数;
(3)把奇次项放在前面是“-”号的括号里,其余的项放在前面是“+”号的括号里.
解:(1)根据题意可得:-(a5-3a3+a2-1);
(2)根据题意可得:-(a5-3a3+a2+2);
(3)根据题意可得:-(a5-3a3)+(-a2+2).
四、典型例题
总结:
在给式子添括号时,括号前的正负号改变,括号内的各项同时变号.
【当堂检测】
3.下列式子中,正确的是( )
A.5x2-3x+7y=5x2-(3x+7y)
B.3x2-3x+7y=3x2-(7y-3x)
C.3x2-4x+2y2 = 3x2-(4x-2y2)
D.5x2-6x-y2 = 5x2-(6x-y2)
C
【当堂检测】
4.把-3x2-4xy+2y2-4x+y+2中的二次项放在前面带有“-”号的括号里,一次项放在前面带有“+”号的括号里.
解:-3x2-4xy+2y2-4x+y+2
=-(3x2+4xy-2y2)+(-4x+y)+2.
四、典型例题
例3.先去括号,再合并同类项.
(1)3a+3(a+1)-4(a-2); (2)4a2-3a+3-3(-a3+2a+1).
解:原式=3a+3a+3-4a+8
=(3a+3a-4a)+(3+8)
= 2a+11;
原式=4a2-3a+3+3a3-6a-3
=4a2+(-3a-6a)+(3-3)+3a3
= 4a2-9a+3a3.
注意:(1)括号前是负号,去括号时不能忘记变号;
(2)括号前有数字,不能漏乘括号前的数字.
【当堂检测】
5.已知a-b=-3,c+d=2,则(b+c)-(a-d)的值为( )
A.1 B.5 C.-5 D.-1
B
【当堂检测】
6.去括号,合并同类项.
(1) (2)-4(3x2-2xy)+5(x2+2xy-7)
解:原式=
=
=
原式=-12x2+8xy+5x2+10xy-35
=(-12x2+5x2)+(8xy+10xy)-35
= -7x2+18xy-35
五、课堂总结
1.去括号法则:
(1)如果括号前面是“+”号,去括号时把括号连同它前面的“+”号去掉,括号内的各项都不改变符号;
(2)如果括号前面是“-”号时,去括号时把括号连同它前面的“-”号去掉,括号内的各项都改变符号.
2.添括号法则:
(1)所添括号前面是“+”号,括到括号里的各项都不改变符号;
(2)所添括号前面是“-”号,括到括号里的各项都改变符号.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
