2.1. 3代数式的值 课件(共17张PPT) 2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 2.1. 3代数式的值 课件(共17张PPT) 2023—2024学年沪科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:18:04 | ||
图片预览






文档简介
(共17张PPT)
第二章 整式加减
2.1 代数式
2.1.3 代数式的值
1.知道代数式的值的概念,会用直接代入法求代数式的值
2.会根据实际问题列代数式并求值,能适当添括号进行整体代入求值
一、学习目标
二、新课导入
一项调查研究显示:一个10~50岁的人,每天所需的睡眠时间t h与他的年龄n岁之间的关系为 .
例如:30岁的人每天所需的睡眠时间为:
(h)
算一算:你每天需要多少睡眠时间?
三、概念剖析
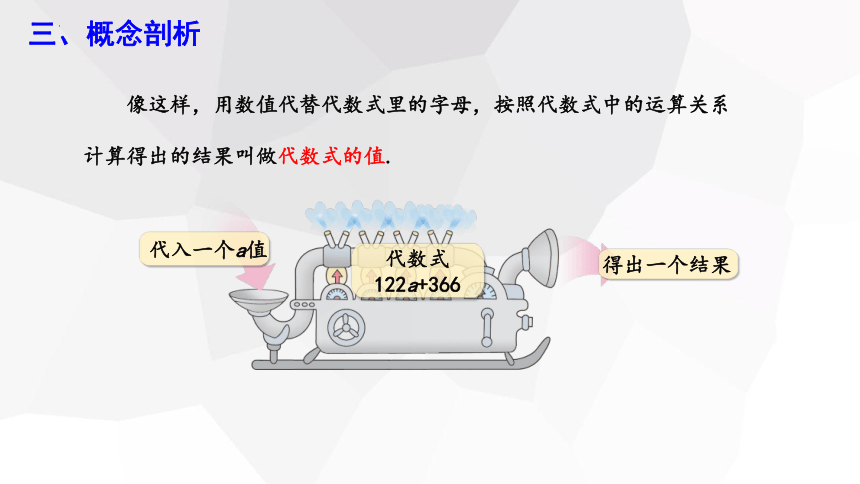
像这样,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.
代入一个a值
代数式
122a+366
得出一个结果
四、典型例题
例1.圆柱的体积等于底面积乘高.若用h表示圆柱的高,r表示底面半径,V表示圆柱的体积.
(1) 请用字母h,r,V写出圆柱的体积公式.
解:∵圆柱的体积等于底面积×高
由题意可知:
圆柱的底面积=πr2
∴V=πr2·h
四、典型例题
例1.圆柱的体积等于底面积乘高.若用h表示圆柱的高,r表示底面半径,V表示圆柱的体积.
(2) 求底面半径为50cm,高为20cm的圆柱的体积.
解:由(1)可知:V=πr2·h
当r=50,h=20时
V=502π×20
=50000π(cm3)
答:圆柱的体积为50000π cm3
四、典型例题
例2.某种商品大袋装4.8元一袋,小袋装3.6元一袋;若在一个月内的销售量是大袋m袋,小袋n袋;
(1)用式子表示在这个月内销售这种商品的收入;
解:由题意可知:
这个月内销售这种商品的收入(4.8m+3.6n)元
四、典型例题
例2.某种商品大袋装4.8元一袋,小袋装3.6元一袋;若在一个月内的销售量是大袋m袋,小袋n袋;
(2)如果这个月卖出大袋20袋,小袋50袋;
那么这个月内销售这种商品的收入是多少?
解:由题意可知当m=20,n=50时
4.8×20+3.6×50=274(元)
答:这个月内销售这种商品的收入是274元.
四、典型例题
注意:代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如例1 V=πr2·h中的字母r、h不能取负数.
【当堂检测】
1.请你用式子表示如图所示的长方体形无盖纸盒的容积(纸盒厚度忽略不计)和表面积;并求出当a=2,b=3,c=4时,纸盒的容积和表面积.
解:根据题意得纸盒的容积v=abc;表面积s=2ab+2bc+ac.
a
b
c
当a=2,b=3,c=4时;v=2×3×4=24,
s=2×2×3+2×3×4+2×4=44
答:无盖纸盒的容积和表面积分别为abc和2ab+2bc+ac;
当a=2,b=3,c=4时,纸盒的容积和表面积分别为24和44.
【当堂检测】
2.三个队植树,第一队植树a棵,第二队植的树比第一队的2倍还多8棵,第三队植的树比第二队的一半少6棵,问三队共植树多少棵 并求当a=100时,三队共植树的棵数.
解:由题意得三队共植树的棵数是:
a+(2a+8)+0.5×(2a+8)-6=(4a+6)(棵)
答:三队共植树(4a+6)棵,当a=100时,三队共植树406棵
当a=100时,4a+6=406(棵)
四、典型例题
例3.(1)当 x=-3时,求 x2 -3x+5 的值;
解:当x = -3 时,
x2-3x+5 =(-3)2-3×(-3)+ 5
=23
(2)当a=0.5,b=-2时,求 的值.
解:当a= 0.5, b=-2时,
四、典型例题
例4.(1)已知x-2y=3,求代数式9-2x+4y的值.
解:当x-2y=3时,
9-2x+4y=9-2(x-2y)
=9-2×3
=3
(2)已知x-3=2,求代数式(x-3)2-2(x-3)+1的值.
解:当x-3=2时,
(x-3)2-2(x-3)+1=22-2×2+1
=1
四、典型例题
归纳:
求代数值的步骤是:
(1)代入;
(2)计算
【当堂检测】
3.如图所示是一个运算程序,若输入的值为-3,则输出的结果为( )
A. -8 B. -4 C. 3 D. 4
分析:-3<0,(-3)2=9,-2×9+10=-8.
A
【当堂检测】
4.(1)当a=-1,b=3时,代数式2a-b的值等于 .
(2)已知x+2y=2,则1-2x-4y的值等于 .
-5
-3
五、课堂总结
通过这节课,你有什么收获?
1.用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.
2.代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义.
第二章 整式加减
2.1 代数式
2.1.3 代数式的值
1.知道代数式的值的概念,会用直接代入法求代数式的值
2.会根据实际问题列代数式并求值,能适当添括号进行整体代入求值
一、学习目标
二、新课导入
一项调查研究显示:一个10~50岁的人,每天所需的睡眠时间t h与他的年龄n岁之间的关系为 .
例如:30岁的人每天所需的睡眠时间为:
(h)
算一算:你每天需要多少睡眠时间?
三、概念剖析
像这样,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.
代入一个a值
代数式
122a+366
得出一个结果
四、典型例题
例1.圆柱的体积等于底面积乘高.若用h表示圆柱的高,r表示底面半径,V表示圆柱的体积.
(1) 请用字母h,r,V写出圆柱的体积公式.
解:∵圆柱的体积等于底面积×高
由题意可知:
圆柱的底面积=πr2
∴V=πr2·h
四、典型例题
例1.圆柱的体积等于底面积乘高.若用h表示圆柱的高,r表示底面半径,V表示圆柱的体积.
(2) 求底面半径为50cm,高为20cm的圆柱的体积.
解:由(1)可知:V=πr2·h
当r=50,h=20时
V=502π×20
=50000π(cm3)
答:圆柱的体积为50000π cm3
四、典型例题
例2.某种商品大袋装4.8元一袋,小袋装3.6元一袋;若在一个月内的销售量是大袋m袋,小袋n袋;
(1)用式子表示在这个月内销售这种商品的收入;
解:由题意可知:
这个月内销售这种商品的收入(4.8m+3.6n)元
四、典型例题
例2.某种商品大袋装4.8元一袋,小袋装3.6元一袋;若在一个月内的销售量是大袋m袋,小袋n袋;
(2)如果这个月卖出大袋20袋,小袋50袋;
那么这个月内销售这种商品的收入是多少?
解:由题意可知当m=20,n=50时
4.8×20+3.6×50=274(元)
答:这个月内销售这种商品的收入是274元.
四、典型例题
注意:代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如例1 V=πr2·h中的字母r、h不能取负数.
【当堂检测】
1.请你用式子表示如图所示的长方体形无盖纸盒的容积(纸盒厚度忽略不计)和表面积;并求出当a=2,b=3,c=4时,纸盒的容积和表面积.
解:根据题意得纸盒的容积v=abc;表面积s=2ab+2bc+ac.
a
b
c
当a=2,b=3,c=4时;v=2×3×4=24,
s=2×2×3+2×3×4+2×4=44
答:无盖纸盒的容积和表面积分别为abc和2ab+2bc+ac;
当a=2,b=3,c=4时,纸盒的容积和表面积分别为24和44.
【当堂检测】
2.三个队植树,第一队植树a棵,第二队植的树比第一队的2倍还多8棵,第三队植的树比第二队的一半少6棵,问三队共植树多少棵 并求当a=100时,三队共植树的棵数.
解:由题意得三队共植树的棵数是:
a+(2a+8)+0.5×(2a+8)-6=(4a+6)(棵)
答:三队共植树(4a+6)棵,当a=100时,三队共植树406棵
当a=100时,4a+6=406(棵)
四、典型例题
例3.(1)当 x=-3时,求 x2 -3x+5 的值;
解:当x = -3 时,
x2-3x+5 =(-3)2-3×(-3)+ 5
=23
(2)当a=0.5,b=-2时,求 的值.
解:当a= 0.5, b=-2时,
四、典型例题
例4.(1)已知x-2y=3,求代数式9-2x+4y的值.
解:当x-2y=3时,
9-2x+4y=9-2(x-2y)
=9-2×3
=3
(2)已知x-3=2,求代数式(x-3)2-2(x-3)+1的值.
解:当x-3=2时,
(x-3)2-2(x-3)+1=22-2×2+1
=1
四、典型例题
归纳:
求代数值的步骤是:
(1)代入;
(2)计算
【当堂检测】
3.如图所示是一个运算程序,若输入的值为-3,则输出的结果为( )
A. -8 B. -4 C. 3 D. 4
分析:-3<0,(-3)2=9,-2×9+10=-8.
A
【当堂检测】
4.(1)当a=-1,b=3时,代数式2a-b的值等于 .
(2)已知x+2y=2,则1-2x-4y的值等于 .
-5
-3
五、课堂总结
通过这节课,你有什么收获?
1.用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值.
2.代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
