2.2.3整式的加减 课件(共17张PPT) 2023—2024学年沪科版数学七年级上册
文档属性
| 名称 | 2.2.3整式的加减 课件(共17张PPT) 2023—2024学年沪科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第二章 整式加减
2.2 整式加减
2.2.3 整式加减
1.会进行整式加减的运算,能将整式进行化简并求值(重点)
2.能将多项式关于某个字母降幂(升幂)排列
3.能用整式加减的混合运算解决相关问题
一、学习目标
二、新课导入
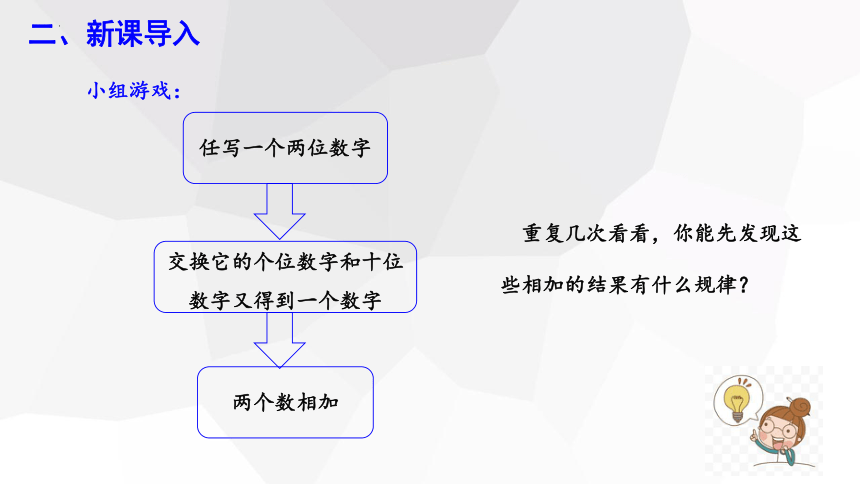
重复几次看看,你能先发现这
些相加的结果有什么规律?
小组游戏:
任写一个两位数字
交换它的个位数字和十位数字又得到一个数字
两个数相加
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个
两位数可以表示为:10a+b,例如37=10×3+7;交换这个两位数的十位
数字和个位数字,得到的数是:10b+a.
将这两个数相加得:(10a+b)+(10b+a)
三、概念剖析
三、概念剖析
接下来我们来计算(10a+b)+(10b+a)
去括号得 =10a+b+10b+a
合并同类项 =(10+1)a+(1+10)b=11a+11b
逆用乘法分配律 =11(a+b)
这时我们就发现这些相加的结果为11的倍数.
三、概念剖析
同样我们来计算(10a+b)-(10b+a)
去括号得 =10a+b-10b-a
合并同类项 =(10-1)a+(1-10)b=9a-9b
逆用乘法分配律 =9(a-b)
如果我们让这两个数相减,又能得到什么结论呢?
这时我们就发现这些相减的结果为9的倍数.
三、概念剖析
上面我们进行了(10a+b)+(10b+a)和(10a+b)-(10b+a)
的计算,这是两个多项式的加减运算.
通过观察计算过程我们发现整式加减步骤为:
1. 列式,要用括号把每个整式括起来;
2. 去括号,遇“+”不变号,遇“–”全变号;
3. 合并同类项.
四、典型例题
例1.化简:
(1)求整式x+2与1-5x的差;
解:(x+2)-(1-5x)
=x+2-1+5x
=(x+5x)+(2-1)
=6x+1
(2)求整式3x2+2x与2(x2-3x)的差;
解:(3x2+2x)-2(x2-3x)
=3x2+2x-2x2+6x
=(3x2-2x2)+(2x+6x)
=x2+8x
总结:
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算;
2.整式的加减运算归结为去括号、合并同类项,运算结果仍是整式.
四、典型例题
3.运算结果,常将多项式按某个字母(如x)的指数从大到小(或从小到大)依次排列,这种排列叫做关于这个字母(如x)的降幂(升幂)排列.
【当堂检测】
1.把下列多项式先按x降幂排列,再按x的升幂排列.
(1)-9x2+12x3y2-5xy+2 (2)12x-5x6+23x4-x2
①按x的降幂排列:
12x3y2-9x2-5xy+2
②按x的升幂排列:
-5xy-9x2+12x3y2+2
①按x的降幂排列:
-5x6+23x4-x2+12x
②按x的升幂排列:
12x-x2+23x4-5x6
【当堂检测】
2.(1)求2x2 -3x + 1与 -3x2 + 5x-7 的和
(2)求5p-3q与3(p2-2q)的差.
解:(2x2–3x+1)+(–3x2+5x–7)
= 2x2–3x+1–3x2+5x–7
= –x2+2x–6
解:(5p-3q)-3(p2-2q)
=5p-3q-3p2+6q
=-3p2+5p+3q
四、典型例题
例2:求 ,其中 .
当 时,
原式=
解:
【当堂检测】
3.先化简下式,再求值:
其中a=-1,b=-2.
解:
当a=-1,b=-2时,
原式
四、典型例题
例3.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和
圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
4.小明、小华、小亮三人每人各点了一份套餐,如下图所示.可乐的价格为x元一杯,汉堡的价格为y元一份,薯条的价格为z元一个;则他们三人各自的套餐价格是多少?三份套餐总价格是多少?
小明的套餐
小华的套餐
小亮的套餐
【当堂检测】
【当堂检测】
小明的套餐
小华的套餐
小亮的套餐
解:小明的套餐价格为:(x+y+z)元
小华的套餐价格为:(x+2y)元
小亮的套餐价格为:(x+z)元
三份套餐总价格为:(x+y+z)+(x+2y)+(x+z)
=x+y+z+x+2y+x+z=(1+1+1)x+(1+2)y+(1+1)z=(3x+3y+2z)元
五、课堂总结
1.整式加减的步骤:
(1)列式,要用括号把每个整式括起来;
(2)去括号,遇“+”不变号,遇“–”全变号;
(3)合并同类项.
2.降幂(升幂)排列:
运算结果常将多项式按某个字母(如x)的指数从大到小(或从小到大)依次排列
第二章 整式加减
2.2 整式加减
2.2.3 整式加减
1.会进行整式加减的运算,能将整式进行化简并求值(重点)
2.能将多项式关于某个字母降幂(升幂)排列
3.能用整式加减的混合运算解决相关问题
一、学习目标
二、新课导入
重复几次看看,你能先发现这
些相加的结果有什么规律?
小组游戏:
任写一个两位数字
交换它的个位数字和十位数字又得到一个数字
两个数相加
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个
两位数可以表示为:10a+b,例如37=10×3+7;交换这个两位数的十位
数字和个位数字,得到的数是:10b+a.
将这两个数相加得:(10a+b)+(10b+a)
三、概念剖析
三、概念剖析
接下来我们来计算(10a+b)+(10b+a)
去括号得 =10a+b+10b+a
合并同类项 =(10+1)a+(1+10)b=11a+11b
逆用乘法分配律 =11(a+b)
这时我们就发现这些相加的结果为11的倍数.
三、概念剖析
同样我们来计算(10a+b)-(10b+a)
去括号得 =10a+b-10b-a
合并同类项 =(10-1)a+(1-10)b=9a-9b
逆用乘法分配律 =9(a-b)
如果我们让这两个数相减,又能得到什么结论呢?
这时我们就发现这些相减的结果为9的倍数.
三、概念剖析
上面我们进行了(10a+b)+(10b+a)和(10a+b)-(10b+a)
的计算,这是两个多项式的加减运算.
通过观察计算过程我们发现整式加减步骤为:
1. 列式,要用括号把每个整式括起来;
2. 去括号,遇“+”不变号,遇“–”全变号;
3. 合并同类项.
四、典型例题
例1.化简:
(1)求整式x+2与1-5x的差;
解:(x+2)-(1-5x)
=x+2-1+5x
=(x+5x)+(2-1)
=6x+1
(2)求整式3x2+2x与2(x2-3x)的差;
解:(3x2+2x)-2(x2-3x)
=3x2+2x-2x2+6x
=(3x2-2x2)+(2x+6x)
=x2+8x
总结:
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算;
2.整式的加减运算归结为去括号、合并同类项,运算结果仍是整式.
四、典型例题
3.运算结果,常将多项式按某个字母(如x)的指数从大到小(或从小到大)依次排列,这种排列叫做关于这个字母(如x)的降幂(升幂)排列.
【当堂检测】
1.把下列多项式先按x降幂排列,再按x的升幂排列.
(1)-9x2+12x3y2-5xy+2 (2)12x-5x6+23x4-x2
①按x的降幂排列:
12x3y2-9x2-5xy+2
②按x的升幂排列:
-5xy-9x2+12x3y2+2
①按x的降幂排列:
-5x6+23x4-x2+12x
②按x的升幂排列:
12x-x2+23x4-5x6
【当堂检测】
2.(1)求2x2 -3x + 1与 -3x2 + 5x-7 的和
(2)求5p-3q与3(p2-2q)的差.
解:(2x2–3x+1)+(–3x2+5x–7)
= 2x2–3x+1–3x2+5x–7
= –x2+2x–6
解:(5p-3q)-3(p2-2q)
=5p-3q-3p2+6q
=-3p2+5p+3q
四、典型例题
例2:求 ,其中 .
当 时,
原式=
解:
【当堂检测】
3.先化简下式,再求值:
其中a=-1,b=-2.
解:
当a=-1,b=-2时,
原式
四、典型例题
例3.一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和
圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
4.小明、小华、小亮三人每人各点了一份套餐,如下图所示.可乐的价格为x元一杯,汉堡的价格为y元一份,薯条的价格为z元一个;则他们三人各自的套餐价格是多少?三份套餐总价格是多少?
小明的套餐
小华的套餐
小亮的套餐
【当堂检测】
【当堂检测】
小明的套餐
小华的套餐
小亮的套餐
解:小明的套餐价格为:(x+y+z)元
小华的套餐价格为:(x+2y)元
小亮的套餐价格为:(x+z)元
三份套餐总价格为:(x+y+z)+(x+2y)+(x+z)
=x+y+z+x+2y+x+z=(1+1+1)x+(1+2)y+(1+1)z=(3x+3y+2z)元
五、课堂总结
1.整式加减的步骤:
(1)列式,要用括号把每个整式括起来;
(2)去括号,遇“+”不变号,遇“–”全变号;
(3)合并同类项.
2.降幂(升幂)排列:
运算结果常将多项式按某个字母(如x)的指数从大到小(或从小到大)依次排列
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
