江苏省南京市金陵汇文学校2023~2024学年九年级上学期12月月考数学试卷(无答案)
文档属性
| 名称 | 江苏省南京市金陵汇文学校2023~2024学年九年级上学期12月月考数学试卷(无答案) |  | |
| 格式 | |||
| 文件大小 | 468.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 15:18:50 | ||
图片预览

文档简介
数 学
(满分 120分,考试时间 120分钟)
一、选择题(本大题共 6 小题,每小题 2 分,共 12 分.在每个小题所给出的四个选项中,
恰有一项符合题目要求,请将正确选项前的字母代号填涂在答题卡相应位置上)
1. 一元二次方程 x(x-1)=0的根是
A.x=1 B.x=0 C.x1=2,x2=1 D.x1=0,x2=1
2. 平面内,若⊙O的半径为 2,OP= 3,则点 P在⊙O
A.内 B.上 C.外 D.内或外
3.若二次函数 y=ax2的图象经过点 P(-2,4),则该图象必经过点
A.(-4,2) B.(-2,-4) C.(2,4) D.(4,-2)[来源:Zxx
4.某班 9名学生参加定点投篮测试,每人投篮 10次,投中的次数统计如下:
3,6,4,6,4,3,6,5,7.这组数据的中位数和众数分别是
A.5,4 B.5,6 C.6,5 D.6,6
5.如图,二次函数 y=ax2+bx+c的图象经过 A(1,0),B(5,0),下列说法正确的是
A.c<0 B.b2-4ac<0
C.a-b+c<0 D.图象的对称轴是直线 x=3
(第 5题) (第 6题)
6.如图,已知点 C为圆锥母线 SB的中点,AB为底面圆的直径,SB=6,AB=4.一只蚂
蚁沿着圆锥的侧面从 A点爬到 C点,则蚂蚁爬行的最短路程为
A.5 B.3 3 C.3 2 D. 6 3
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分.不需要写出解答过程,请把答案
直接填写在答题卡相应位置上)
7.二次函数 y=(x+1)2+2图象的顶点坐标为 ▲ .
8.一组数据:2,3,-1,5的极差为 ▲ .
9.已知 x1、x2是方程 x2-2x-4=0的两个根,则 x1+x2-x1x2的值为 ▲ .
10.在平面直角坐标系中,将二次函数 y=2x2的图象向右平移 3个单位,再向上平移 1个
单位,则平移后的图象所对应的函数表达式为 ▲ .
第 1 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
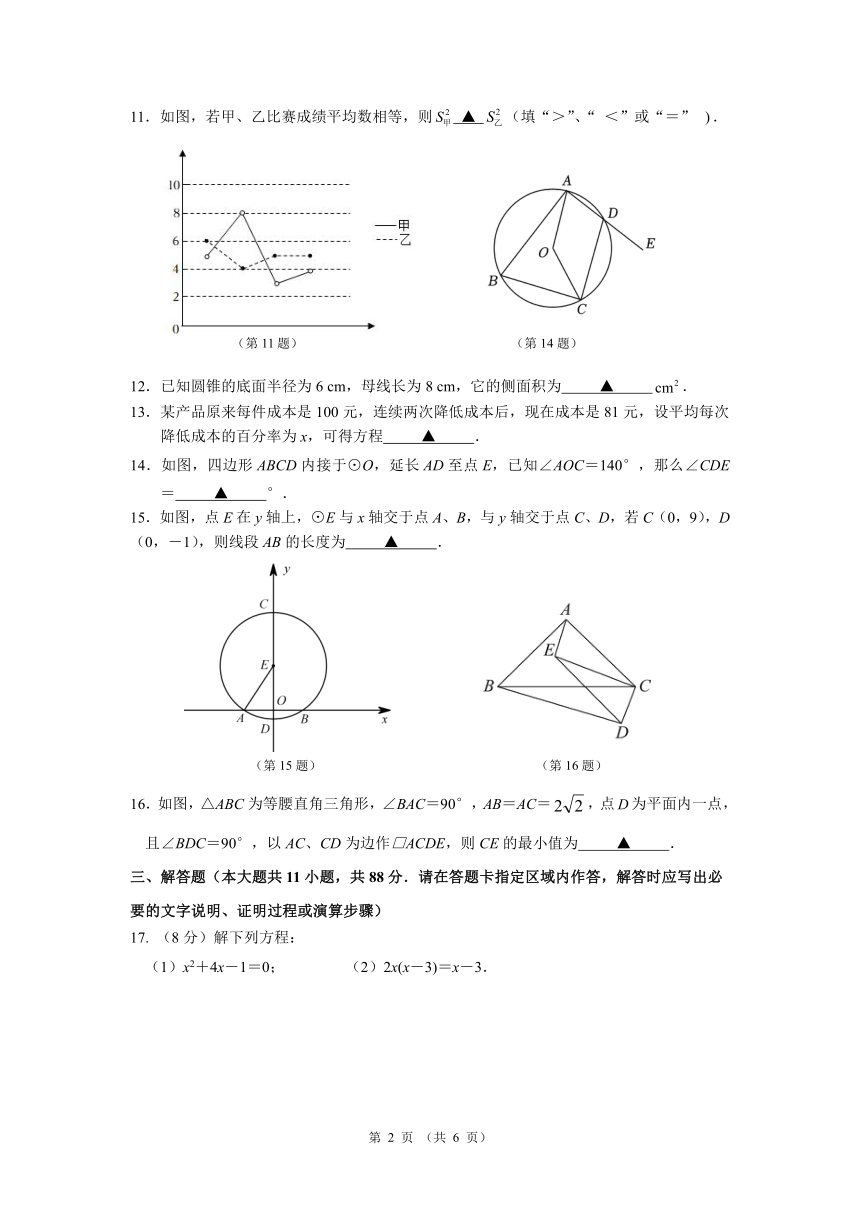
11.如图,若甲、乙比赛成绩平均数相等,则 S 2 ▲ S 2甲 乙(填“>”、“ <”或“=” ).
(第 11题) (第 14题)
12.已知圆锥的底面半径为 6 cm,母线长为 8 cm,它的侧面积为 ▲ cm2.
13.某产品原来每件成本是 100元,连续两次降低成本后,现在成本是 81元,设平均每次
降低成本的百分率为 x,可得方程 ▲ .
14.如图,四边形 ABCD内接于⊙O,延长 AD至点 E,已知∠AOC=140°,那么∠CDE
= ▲ °.
15.如图,点 E在 y轴上,⊙E与 x轴交于点 A、B,与 y轴交于点 C、D,若 C(0,9),D
(0,-1),则线段 AB的长度为 ▲ .
(第 15题) (第 16题)
16.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC= 2 2,点D为平面内一点,
且∠BDC=90°,以 AC、CD为边作□ACDE,则 CE的最小值为 ▲ .
三、解答题(本大题共 11 小题,共 88 分.请在答题卡指定区域内作答,解答时应写出必
要的文字说明、证明过程或演算步骤)
17. (8分)解下列方程:
(1)x2+4x-1=0; (2)2x(x-3)=x-3.
第 2 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
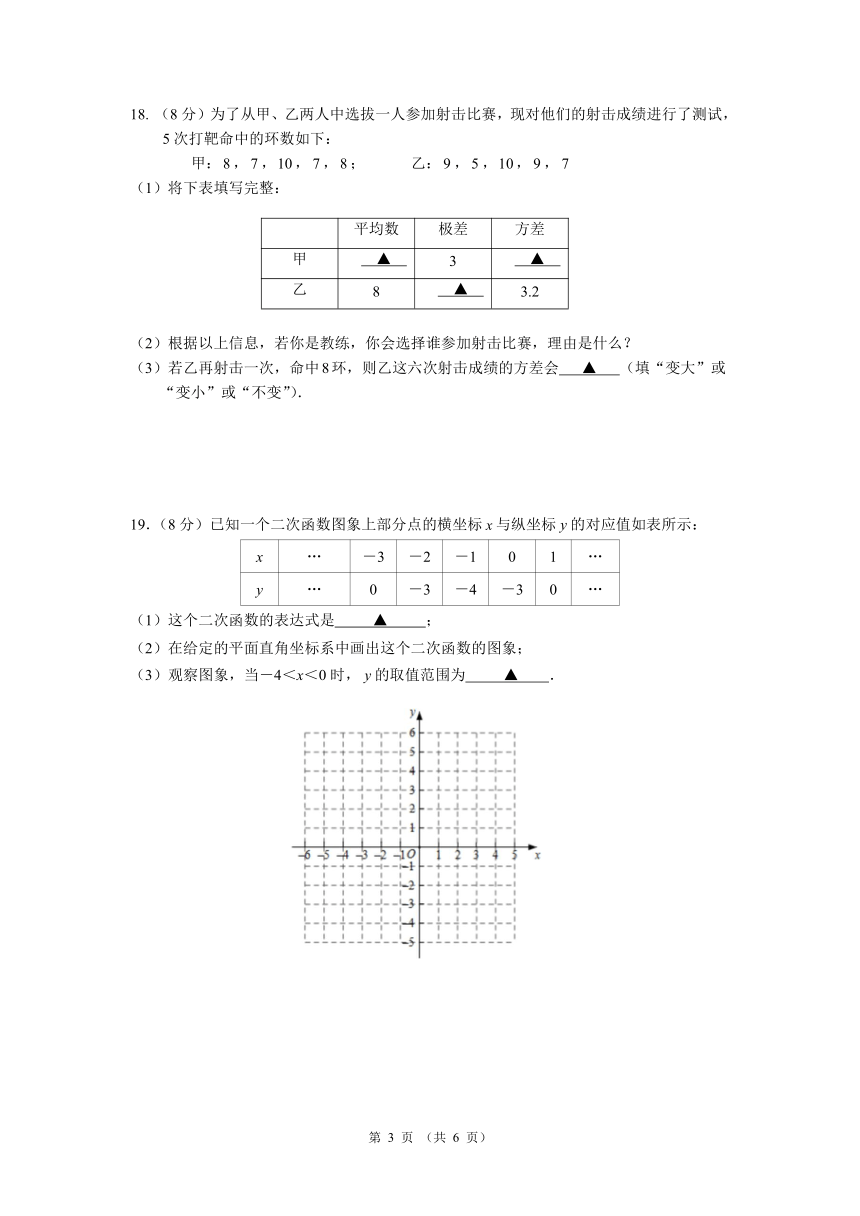
18. (8分)为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,
5次打靶命中的环数如下:
甲:8, 7,10, 7,8; 乙: 9,5,10, 9, 7
(1)将下表填写完整:
平均数 极差 方差
甲 ▲ 3 ▲
乙 8 ▲ 3.2
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 ▲ (填“变大”或
“变小”或“不变”).
19.(8分)已知一个二次函数图象上部分点的横坐标 x与纵坐标 y的对应值如表所示:
x … -3 -2 -1 0 1 …
y … 0 -3 -4 -3 0 …
(1)这个二次函数的表达式是 ▲ ;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)观察图象,当-4<x<0时, y的取值范围为 ▲ .
第 3 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
20.(7分)如图,在⊙O中,AB=AC.
1 BOC 100 ⌒( )若∠ = °,则AB的度数为 ▲ °;
(2)若 AB=13,BC=10,求⊙O的半径.
21.(6分)如图,已知线段 a及∠ACB.
请仅用直.尺.和.圆.规.作⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分
别相切.(不.写.作.法.,.保.留.作.图.痕.迹.).
22.(8分)若关于 x的方程 x2+bx+c=0 有两个实数根,且其中一个根比另一个根大 2,
那么称这样的方程为“隔根方程”.例如,方程 x2+2x=0的两个根是 x1=0,x2=-2,
则方程 x2+2x=0是“隔根方程”.
(1)方程 x2-x-20=0是“隔根方程”吗?判断并说明理由;
(2)若关于 x的方程 x2+mx+m-1=0是“隔根方程”,求 m的值.
第 4 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
23 8 ⌒.( 分)如图,四边形 ABCD是⊙O的内接四边形,AB是直径,C是BD的中点,过点 C
作 CE⊥AD交 AD的延长线于点 E.
(1)求证:CE是⊙O的切线;
(2)若 BC=6,AC=8,求 CE、DE的长.
24.(9分)某淘宝网店销售台灯,成本为每个 30元.销售大数据分析表明:当每个台灯售
价为 40元时,平均每月售出 600个;若售价每下降 1元,其月销售量就增加 200个.
(1)若售价下降 1元,每月能售出 ▲ 个台灯,若售价下降 x元(x>0),每月能售出
▲ 个台灯;
(2)为迎接“双十一”,该网店决定降价促销,在库存为 1210个台灯的情况下,若预计月获
利恰好为 8400元,求每个台灯的售价.
25. (8分)已知二次函数 y=(x-m)2-1(m为常数).
(1)求证:不论 m为何值,该函数图象与 x轴总有两个公共点;
(2)当-1≤x≤3时,y的最小值为 3,求 m的值.
第 5 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
26.(8分)掷实心球是南京市高中阶段学校招生体育考试的选考项目.如图 1,一名女生投
掷实心球,实心球行进路线是一条抛物线,行进高度 y(m)与水平距离 x(m)之间的函数
关系如图 2所示,已知掷出时起点处高度为 5m,当水平距离为 3 m时,实心球行进至最高
3
点 3 m处.
(1)求 y关于 x的函数表达式;
(2)根据南京市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点
到落地点的水平距离大于等于 6.9 m,此项考试得分为满分.该女生在此项考试中是否得满
分,请说明理由.
图 1 图 2
27.(10分)在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面
内,一组对角互补的四边形的四个顶点共圆.请运.用.此.结.论.,解决以下问题:
如图 1,△ABC中,AB=AC,∠BAC=α(60°<α<180°).点 D是 BC边上的一动
点(点 D不与 B、C重合),将线段 AD绕点 A顺时针旋转α到线段 AE,连接 BE.
(1)求证:A、E、B、D四点共圆;
(2)如图 2,当 AD=CD时,⊙O是四边形 AEBD的外接圆,求证:AC是⊙O的切线;
(3)已知α=120°,BC=6,点 M是边 BC的中点,此时⊙P是四边形 AEBD的外接圆,
直接写出圆心 P与点 M距离的最小值.
图 1 图 2 备用图
第 6 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
(满分 120分,考试时间 120分钟)
一、选择题(本大题共 6 小题,每小题 2 分,共 12 分.在每个小题所给出的四个选项中,
恰有一项符合题目要求,请将正确选项前的字母代号填涂在答题卡相应位置上)
1. 一元二次方程 x(x-1)=0的根是
A.x=1 B.x=0 C.x1=2,x2=1 D.x1=0,x2=1
2. 平面内,若⊙O的半径为 2,OP= 3,则点 P在⊙O
A.内 B.上 C.外 D.内或外
3.若二次函数 y=ax2的图象经过点 P(-2,4),则该图象必经过点
A.(-4,2) B.(-2,-4) C.(2,4) D.(4,-2)[来源:Zxx
4.某班 9名学生参加定点投篮测试,每人投篮 10次,投中的次数统计如下:
3,6,4,6,4,3,6,5,7.这组数据的中位数和众数分别是
A.5,4 B.5,6 C.6,5 D.6,6
5.如图,二次函数 y=ax2+bx+c的图象经过 A(1,0),B(5,0),下列说法正确的是
A.c<0 B.b2-4ac<0
C.a-b+c<0 D.图象的对称轴是直线 x=3
(第 5题) (第 6题)
6.如图,已知点 C为圆锥母线 SB的中点,AB为底面圆的直径,SB=6,AB=4.一只蚂
蚁沿着圆锥的侧面从 A点爬到 C点,则蚂蚁爬行的最短路程为
A.5 B.3 3 C.3 2 D. 6 3
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分.不需要写出解答过程,请把答案
直接填写在答题卡相应位置上)
7.二次函数 y=(x+1)2+2图象的顶点坐标为 ▲ .
8.一组数据:2,3,-1,5的极差为 ▲ .
9.已知 x1、x2是方程 x2-2x-4=0的两个根,则 x1+x2-x1x2的值为 ▲ .
10.在平面直角坐标系中,将二次函数 y=2x2的图象向右平移 3个单位,再向上平移 1个
单位,则平移后的图象所对应的函数表达式为 ▲ .
第 1 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
11.如图,若甲、乙比赛成绩平均数相等,则 S 2 ▲ S 2甲 乙(填“>”、“ <”或“=” ).
(第 11题) (第 14题)
12.已知圆锥的底面半径为 6 cm,母线长为 8 cm,它的侧面积为 ▲ cm2.
13.某产品原来每件成本是 100元,连续两次降低成本后,现在成本是 81元,设平均每次
降低成本的百分率为 x,可得方程 ▲ .
14.如图,四边形 ABCD内接于⊙O,延长 AD至点 E,已知∠AOC=140°,那么∠CDE
= ▲ °.
15.如图,点 E在 y轴上,⊙E与 x轴交于点 A、B,与 y轴交于点 C、D,若 C(0,9),D
(0,-1),则线段 AB的长度为 ▲ .
(第 15题) (第 16题)
16.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC= 2 2,点D为平面内一点,
且∠BDC=90°,以 AC、CD为边作□ACDE,则 CE的最小值为 ▲ .
三、解答题(本大题共 11 小题,共 88 分.请在答题卡指定区域内作答,解答时应写出必
要的文字说明、证明过程或演算步骤)
17. (8分)解下列方程:
(1)x2+4x-1=0; (2)2x(x-3)=x-3.
第 2 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
18. (8分)为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,
5次打靶命中的环数如下:
甲:8, 7,10, 7,8; 乙: 9,5,10, 9, 7
(1)将下表填写完整:
平均数 极差 方差
甲 ▲ 3 ▲
乙 8 ▲ 3.2
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 ▲ (填“变大”或
“变小”或“不变”).
19.(8分)已知一个二次函数图象上部分点的横坐标 x与纵坐标 y的对应值如表所示:
x … -3 -2 -1 0 1 …
y … 0 -3 -4 -3 0 …
(1)这个二次函数的表达式是 ▲ ;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)观察图象,当-4<x<0时, y的取值范围为 ▲ .
第 3 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
20.(7分)如图,在⊙O中,AB=AC.
1 BOC 100 ⌒( )若∠ = °,则AB的度数为 ▲ °;
(2)若 AB=13,BC=10,求⊙O的半径.
21.(6分)如图,已知线段 a及∠ACB.
请仅用直.尺.和.圆.规.作⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分
别相切.(不.写.作.法.,.保.留.作.图.痕.迹.).
22.(8分)若关于 x的方程 x2+bx+c=0 有两个实数根,且其中一个根比另一个根大 2,
那么称这样的方程为“隔根方程”.例如,方程 x2+2x=0的两个根是 x1=0,x2=-2,
则方程 x2+2x=0是“隔根方程”.
(1)方程 x2-x-20=0是“隔根方程”吗?判断并说明理由;
(2)若关于 x的方程 x2+mx+m-1=0是“隔根方程”,求 m的值.
第 4 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
23 8 ⌒.( 分)如图,四边形 ABCD是⊙O的内接四边形,AB是直径,C是BD的中点,过点 C
作 CE⊥AD交 AD的延长线于点 E.
(1)求证:CE是⊙O的切线;
(2)若 BC=6,AC=8,求 CE、DE的长.
24.(9分)某淘宝网店销售台灯,成本为每个 30元.销售大数据分析表明:当每个台灯售
价为 40元时,平均每月售出 600个;若售价每下降 1元,其月销售量就增加 200个.
(1)若售价下降 1元,每月能售出 ▲ 个台灯,若售价下降 x元(x>0),每月能售出
▲ 个台灯;
(2)为迎接“双十一”,该网店决定降价促销,在库存为 1210个台灯的情况下,若预计月获
利恰好为 8400元,求每个台灯的售价.
25. (8分)已知二次函数 y=(x-m)2-1(m为常数).
(1)求证:不论 m为何值,该函数图象与 x轴总有两个公共点;
(2)当-1≤x≤3时,y的最小值为 3,求 m的值.
第 5 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
26.(8分)掷实心球是南京市高中阶段学校招生体育考试的选考项目.如图 1,一名女生投
掷实心球,实心球行进路线是一条抛物线,行进高度 y(m)与水平距离 x(m)之间的函数
关系如图 2所示,已知掷出时起点处高度为 5m,当水平距离为 3 m时,实心球行进至最高
3
点 3 m处.
(1)求 y关于 x的函数表达式;
(2)根据南京市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点
到落地点的水平距离大于等于 6.9 m,此项考试得分为满分.该女生在此项考试中是否得满
分,请说明理由.
图 1 图 2
27.(10分)在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面
内,一组对角互补的四边形的四个顶点共圆.请运.用.此.结.论.,解决以下问题:
如图 1,△ABC中,AB=AC,∠BAC=α(60°<α<180°).点 D是 BC边上的一动
点(点 D不与 B、C重合),将线段 AD绕点 A顺时针旋转α到线段 AE,连接 BE.
(1)求证:A、E、B、D四点共圆;
(2)如图 2,当 AD=CD时,⊙O是四边形 AEBD的外接圆,求证:AC是⊙O的切线;
(3)已知α=120°,BC=6,点 M是边 BC的中点,此时⊙P是四边形 AEBD的外接圆,
直接写出圆心 P与点 M距离的最小值.
图 1 图 2 备用图
第 6 页 (共 6 页)
{#{QQABZQQUogAAAAAAARgCQQloCEOQkBCCCIoOwBAAIAAAQQNABAA=}#}
同课章节目录
