第8章 整式乘法和因式分解单元素养综合检测试题(含答案)
文档属性
| 名称 | 第8章 整式乘法和因式分解单元素养综合检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024沪科版数学七年级下册
第8章 整式乘法与因式分解
第8章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023安徽淮北月考)计算-2a3·3a2的结果是( )
A.-5a5 B.-5a6
C.-6a5 D.-6a6
2.(2023浙江绍兴中考)下列计算正确的是( )
A.a6÷a2=a3 B.(-a2)5=-a7
C.(a+1)(a-1)=a2-1 D.(a+1)2=a2+1
3.(2022江苏徐州期末)下列式子中,计算结果为x2+4x-21的是( )
A.(x+7)(x-3) B.(x-7)(x+3)
C.(x+7)(x+3) D.(x-7)(x-3)
4.(2023贵州六盘水期中)小明在做作业的时候,不小心把墨汁滴到了作业本上,×3ab=6ab-3ab3,阴影部分为被墨汁弄污的部分,那么被墨汁遮住的一项是(M7208003)( )
A.(2-b2) B.(2+2b)
C.(3ab+2b2) D.(2ab+b2)
5.(2023四川南充中考)关于x,y的方程组的解满足x+y=1,则4m÷2n的值是(M7208001)( )
A.1 B.2 C.4 D.8
6.【新考向·代数推理】若(a-b)2=4(1-a)(b-1),则下列正确的是( )
A.a+b=1 B.a+b=2 C.a-b=1 D.a-b=2
7.(2023安徽芜湖无为月考)计算:a×1 0012-a×9992=( )
A.5 000a B.1 999a C.10 001a D.10 000a
8.【一题多解】(2023安徽滁州期中)如图,大正方形与小正方形的面积之差是64,则阴影部分的面积是( )
A.32 B.28 C.24 D.16
二、填空题(每小题4分,共16分)
9.(2023安徽淮南二模)因式分解:-mn2+mn-m= .
10.一个多项式除以3xy的商为9x2y-xy,则这个多项式是 .
11.【真实情境】(2023安徽合肥期中)中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.22纳米=0.000 000 022米,将0.000 000 022用科学记数法表示为 .
12.(2023安徽合肥寿春中学期中)有甲、乙、丙三种纸片若干张(如图,a>b).
(1)若用这三种纸片紧密拼接成一个边长为(2a+b)的大正方形,则需要甲种纸片 张.
(2)取三种纸片若干张(三种纸片都要取到),拼成一个长方形,使其面积为a2+nab+24b2,则n的整数值有 个.
三、解答题(共60分)
13.(2023安徽宿州月考)(6分)计算:-22+(π-2 023)0-
14.(2023辽宁沈阳期末)(8分)先化简,再求值:(x-2)2-4x(x-1)+(2x+1)(2x-1),其中x=3.
15.(2023湖南永州期中)(10分)若(x2-3x+q)的展开式中不含x项与 x3项.
(1)求p、q的值;
(2)求代数式(-2p2q)2+3pq的值.
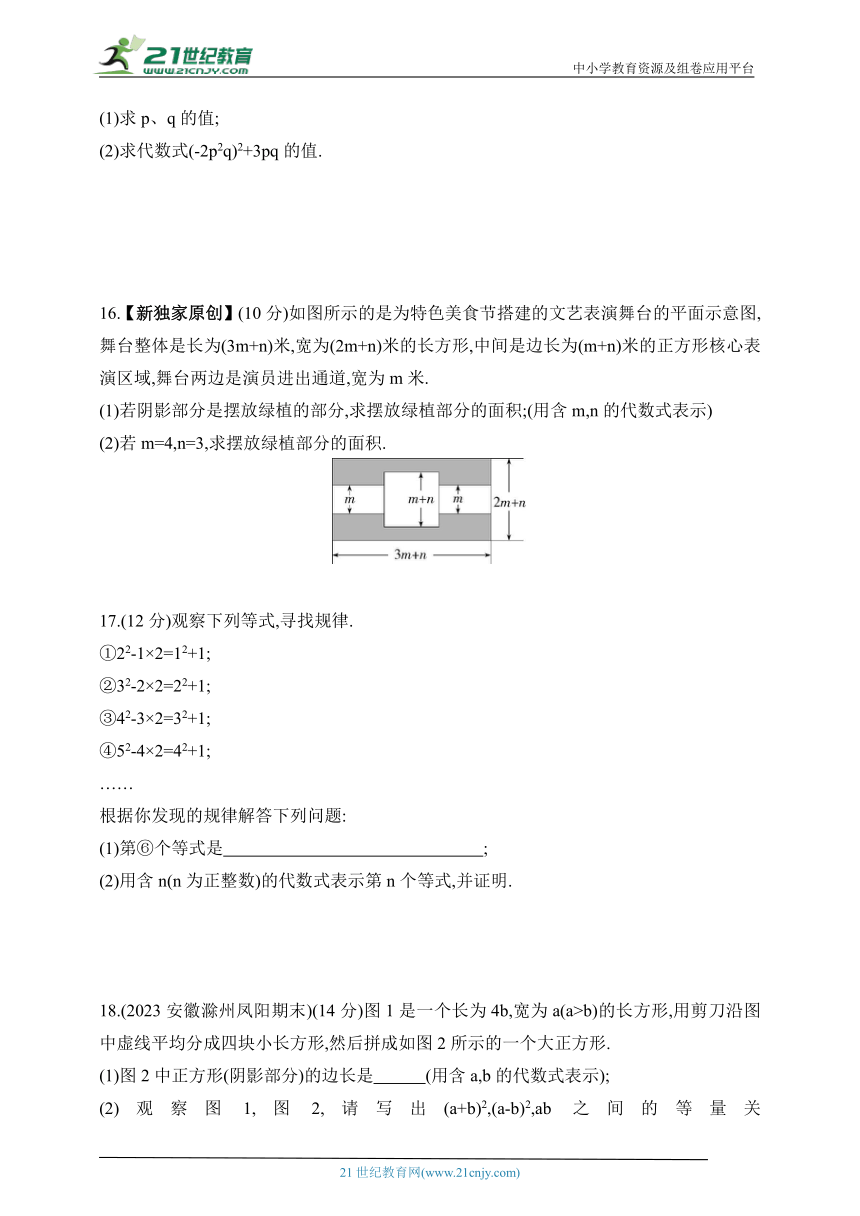
16.【新独家原创】(10分)如图所示的是为特色美食节搭建的文艺表演舞台的平面示意图,舞台整体是长为(3m+n)米,宽为(2m+n)米的长方形,中间是边长为(m+n)米的正方形核心表演区域,舞台两边是演员进出通道,宽为m米.
(1)若阴影部分是摆放绿植的部分,求摆放绿植部分的面积;(用含m,n的代数式表示)
(2)若m=4,n=3,求摆放绿植部分的面积.
17.(12分)观察下列等式,寻找规律.
①22-1×2=12+1;
②32-2×2=22+1;
③42-3×2=32+1;
④52-4×2=42+1;
……
根据你发现的规律解答下列问题:
(1)第⑥个等式是 ;
(2)用含n(n为正整数)的代数式表示第n个等式,并证明.
18.(2023安徽滁州凤阳期末)(14分)图1是一个长为4b,宽为a(a>b)的长方形,用剪刀沿图中虚线平均分成四块小长方形,然后拼成如图2所示的一个大正方形.
(1)图2中正方形(阴影部分)的边长是 (用含a,b的代数式表示);
(2)观察图1,图2,请写出(a+b)2,(a-b)2,ab之间的等量关系: ;
(3)已知(m+n)2=25,(m-n)2=16,求m2+n2的值;
(4)如图3,C是线段AB上的一点,以AC,BC为边向上分别作正方形ACDE和正方形BCFG,连接AF,若AB=7,DF=3,求三角形ACF的面积.
图1 图2 图3
第8章 整式乘法与因式分解
第8章 素养综合检测全练版P59
1.C 原式=(-2)×3·a3+2=-6a5.
2.C a6÷a2=a4,(-a2)5=-a10,(a+1)(a-1)=a2-1,(a+1)2=a2+2a+1.综上所述,选项C正确.
3.A (x+7)(x-3)=x2+4x-21,(x-7)(x+3)=x2-4x-21,(x+7)(x+3)=x2+10x+21,(x-7)(x-3)=x2-10x+21.故选A.
4.A 由题意得=(6ab-3ab3)÷(3ab)=6ab÷(3ab)-3ab3÷(3ab)=2-b2.
5.D 解方程组
由①-②,得2x+2y=2m-n-1,
因为x+y=1,
所以2m-n-1=2,即2m-n=3,
所以4m÷2n=22m÷2n=22m-n=23=8.
6.B 由题意,得(a-b)2+4(a-1)(b-1)=0,
所以(a-b)2+4ab-4(a+b)+4=0,
所以(a+b)2-4(a+b)+4=0,
所以(a+b-2)2=0,
所以a+b=2.
7.D 原式=a(1 0012-9992)=a(1 001+999)·(1 001-999)=a×2 000×2=10 000a.
8.A 设大正方形的边长为a,小正方形的边长为b,则a2-b2=64.
方法一:S阴影=S三角形ACG+S三角形AEG=AG·(CD+DE)=(a-b)(a+b)=(a2-b2)=×64=32.
方法二:S阴影=S三角形ACE-S三角形CEG=a(a+b)-b(a+b)=(a+b)(a-b)=(a2-b2)=×64=32.
9. 答案 -m
解析 原式=-m
=-m.
10. 答案 27x3y2-x2y2
解析 根据题意得这个多项式为3xy=27x3y2-x2y2.
11. 答案 2.2×10-8
解析 用科学记数法表示绝对值小于1的数的一般形式为±a×10-n,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),则0.000 000 022=2.2×10-8.
12. 答案 (1)4 (2)4
解析 (1)大正方形的面积为(2a+b)2=4a2+4ab+b2,所以需要甲种纸片4张,乙种纸片4张,丙种纸片1张.
(2)因为24=1×24=2×12=3×8=4×6,所以n=1+24=25或n=2+12=14或n=3+8=11或n=4+6=10,所以n的整数值有4个.
13. 解析 原式=-4+1-(-2)=-4+1+2=-1.
14. 解析 原式=x2-4x+4-4x2+4x+4x2-1=x2+3,
当x=3时,原式=32+3=9+3=12.
15. 解析 (1)因为(x2-3x+q)的展开式中不含x项和x3项,原式=x4-3x3+qx2+px3-3px2+pqx-x2+x-q=x4+(-3+p)x3+x2+(pq+1)x-q,
所以-3+p=0,pq+1=0,
所以p=3,q=-.
(2)由(1)知p=3,q=-,
所以(-2p2q)2+3pq=4p4q2+3pq
=4×34×+3×3×
=4×81×-3=36-3=33.
16. 解析 (1)根据题意,得摆放绿植部分的面积为(3m+n)(2m+n)-(m+n)2-m[(3m+n)-(m+n)]=6m2+5mn+n2-m2-2mn-n2-2m2=(3m2+3mn)平方米.
答:摆放绿植部分的面积为(3m2+3mn)平方米.
(2)当m=4,n=3时,
3m2+3mn=3m(m+n)=3×4×(4+3)=84(平方米).
答:摆放绿植部分的面积为84平方米.
17. 解析 (1)根据规律得第⑥个等式为72-6×2=62+1.
故答案为72-6×2=62+1.
(2)(n+1)2-2n=n2+1.
证明:左边=n2+2n+1-2n=n2+1,右边=n2+1,
所以左边=右边,所以等式成立.
18. 解析 (1)a-b.
(2)(a+b)2-4ab=(a-b)2.
(3)因为(m+n)2=25,
所以m2+2mn+n2=25①,
因为(m-n)2=16,
所以m2-2mn+n2=16②,
①+②得2(m2+n2)=41,所以m2+n2=.
(4)设正方形ACDE的边长为x,正方形BCFG的边长为y,所以x+y=7,x-y=3,因为(x+y)2=(x-y)2+4xy,
所以72=32+4xy,所以xy=10,
所以=AC·CF=xy=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版数学七年级下册
第8章 整式乘法与因式分解
第8章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023安徽淮北月考)计算-2a3·3a2的结果是( )
A.-5a5 B.-5a6
C.-6a5 D.-6a6
2.(2023浙江绍兴中考)下列计算正确的是( )
A.a6÷a2=a3 B.(-a2)5=-a7
C.(a+1)(a-1)=a2-1 D.(a+1)2=a2+1
3.(2022江苏徐州期末)下列式子中,计算结果为x2+4x-21的是( )
A.(x+7)(x-3) B.(x-7)(x+3)
C.(x+7)(x+3) D.(x-7)(x-3)
4.(2023贵州六盘水期中)小明在做作业的时候,不小心把墨汁滴到了作业本上,×3ab=6ab-3ab3,阴影部分为被墨汁弄污的部分,那么被墨汁遮住的一项是(M7208003)( )
A.(2-b2) B.(2+2b)
C.(3ab+2b2) D.(2ab+b2)
5.(2023四川南充中考)关于x,y的方程组的解满足x+y=1,则4m÷2n的值是(M7208001)( )
A.1 B.2 C.4 D.8
6.【新考向·代数推理】若(a-b)2=4(1-a)(b-1),则下列正确的是( )
A.a+b=1 B.a+b=2 C.a-b=1 D.a-b=2
7.(2023安徽芜湖无为月考)计算:a×1 0012-a×9992=( )
A.5 000a B.1 999a C.10 001a D.10 000a
8.【一题多解】(2023安徽滁州期中)如图,大正方形与小正方形的面积之差是64,则阴影部分的面积是( )
A.32 B.28 C.24 D.16
二、填空题(每小题4分,共16分)
9.(2023安徽淮南二模)因式分解:-mn2+mn-m= .
10.一个多项式除以3xy的商为9x2y-xy,则这个多项式是 .
11.【真实情境】(2023安徽合肥期中)中国第55颗北斗导航卫星成功发射,顺利完成全球组网.其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片,已实现规模化应用.22纳米=0.000 000 022米,将0.000 000 022用科学记数法表示为 .
12.(2023安徽合肥寿春中学期中)有甲、乙、丙三种纸片若干张(如图,a>b).
(1)若用这三种纸片紧密拼接成一个边长为(2a+b)的大正方形,则需要甲种纸片 张.
(2)取三种纸片若干张(三种纸片都要取到),拼成一个长方形,使其面积为a2+nab+24b2,则n的整数值有 个.
三、解答题(共60分)
13.(2023安徽宿州月考)(6分)计算:-22+(π-2 023)0-
14.(2023辽宁沈阳期末)(8分)先化简,再求值:(x-2)2-4x(x-1)+(2x+1)(2x-1),其中x=3.
15.(2023湖南永州期中)(10分)若(x2-3x+q)的展开式中不含x项与 x3项.
(1)求p、q的值;
(2)求代数式(-2p2q)2+3pq的值.
16.【新独家原创】(10分)如图所示的是为特色美食节搭建的文艺表演舞台的平面示意图,舞台整体是长为(3m+n)米,宽为(2m+n)米的长方形,中间是边长为(m+n)米的正方形核心表演区域,舞台两边是演员进出通道,宽为m米.
(1)若阴影部分是摆放绿植的部分,求摆放绿植部分的面积;(用含m,n的代数式表示)
(2)若m=4,n=3,求摆放绿植部分的面积.
17.(12分)观察下列等式,寻找规律.
①22-1×2=12+1;
②32-2×2=22+1;
③42-3×2=32+1;
④52-4×2=42+1;
……
根据你发现的规律解答下列问题:
(1)第⑥个等式是 ;
(2)用含n(n为正整数)的代数式表示第n个等式,并证明.
18.(2023安徽滁州凤阳期末)(14分)图1是一个长为4b,宽为a(a>b)的长方形,用剪刀沿图中虚线平均分成四块小长方形,然后拼成如图2所示的一个大正方形.
(1)图2中正方形(阴影部分)的边长是 (用含a,b的代数式表示);
(2)观察图1,图2,请写出(a+b)2,(a-b)2,ab之间的等量关系: ;
(3)已知(m+n)2=25,(m-n)2=16,求m2+n2的值;
(4)如图3,C是线段AB上的一点,以AC,BC为边向上分别作正方形ACDE和正方形BCFG,连接AF,若AB=7,DF=3,求三角形ACF的面积.
图1 图2 图3
第8章 整式乘法与因式分解
第8章 素养综合检测全练版P59
1.C 原式=(-2)×3·a3+2=-6a5.
2.C a6÷a2=a4,(-a2)5=-a10,(a+1)(a-1)=a2-1,(a+1)2=a2+2a+1.综上所述,选项C正确.
3.A (x+7)(x-3)=x2+4x-21,(x-7)(x+3)=x2-4x-21,(x+7)(x+3)=x2+10x+21,(x-7)(x-3)=x2-10x+21.故选A.
4.A 由题意得=(6ab-3ab3)÷(3ab)=6ab÷(3ab)-3ab3÷(3ab)=2-b2.
5.D 解方程组
由①-②,得2x+2y=2m-n-1,
因为x+y=1,
所以2m-n-1=2,即2m-n=3,
所以4m÷2n=22m÷2n=22m-n=23=8.
6.B 由题意,得(a-b)2+4(a-1)(b-1)=0,
所以(a-b)2+4ab-4(a+b)+4=0,
所以(a+b)2-4(a+b)+4=0,
所以(a+b-2)2=0,
所以a+b=2.
7.D 原式=a(1 0012-9992)=a(1 001+999)·(1 001-999)=a×2 000×2=10 000a.
8.A 设大正方形的边长为a,小正方形的边长为b,则a2-b2=64.
方法一:S阴影=S三角形ACG+S三角形AEG=AG·(CD+DE)=(a-b)(a+b)=(a2-b2)=×64=32.
方法二:S阴影=S三角形ACE-S三角形CEG=a(a+b)-b(a+b)=(a+b)(a-b)=(a2-b2)=×64=32.
9. 答案 -m
解析 原式=-m
=-m.
10. 答案 27x3y2-x2y2
解析 根据题意得这个多项式为3xy=27x3y2-x2y2.
11. 答案 2.2×10-8
解析 用科学记数法表示绝对值小于1的数的一般形式为±a×10-n,其中1≤a<10,n是正整数,n等于原数中第一个不等于零的数字前面的零的个数(包括小数点前面的一个零),则0.000 000 022=2.2×10-8.
12. 答案 (1)4 (2)4
解析 (1)大正方形的面积为(2a+b)2=4a2+4ab+b2,所以需要甲种纸片4张,乙种纸片4张,丙种纸片1张.
(2)因为24=1×24=2×12=3×8=4×6,所以n=1+24=25或n=2+12=14或n=3+8=11或n=4+6=10,所以n的整数值有4个.
13. 解析 原式=-4+1-(-2)=-4+1+2=-1.
14. 解析 原式=x2-4x+4-4x2+4x+4x2-1=x2+3,
当x=3时,原式=32+3=9+3=12.
15. 解析 (1)因为(x2-3x+q)的展开式中不含x项和x3项,原式=x4-3x3+qx2+px3-3px2+pqx-x2+x-q=x4+(-3+p)x3+x2+(pq+1)x-q,
所以-3+p=0,pq+1=0,
所以p=3,q=-.
(2)由(1)知p=3,q=-,
所以(-2p2q)2+3pq=4p4q2+3pq
=4×34×+3×3×
=4×81×-3=36-3=33.
16. 解析 (1)根据题意,得摆放绿植部分的面积为(3m+n)(2m+n)-(m+n)2-m[(3m+n)-(m+n)]=6m2+5mn+n2-m2-2mn-n2-2m2=(3m2+3mn)平方米.
答:摆放绿植部分的面积为(3m2+3mn)平方米.
(2)当m=4,n=3时,
3m2+3mn=3m(m+n)=3×4×(4+3)=84(平方米).
答:摆放绿植部分的面积为84平方米.
17. 解析 (1)根据规律得第⑥个等式为72-6×2=62+1.
故答案为72-6×2=62+1.
(2)(n+1)2-2n=n2+1.
证明:左边=n2+2n+1-2n=n2+1,右边=n2+1,
所以左边=右边,所以等式成立.
18. 解析 (1)a-b.
(2)(a+b)2-4ab=(a-b)2.
(3)因为(m+n)2=25,
所以m2+2mn+n2=25①,
因为(m-n)2=16,
所以m2-2mn+n2=16②,
①+②得2(m2+n2)=41,所以m2+n2=.
(4)设正方形ACDE的边长为x,正方形BCFG的边长为y,所以x+y=7,x-y=3,因为(x+y)2=(x-y)2+4xy,
所以72=32+4xy,所以xy=10,
所以=AC·CF=xy=5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
