第10章 相交线、平行线和平移单元素养综合检测试题(含答案)
文档属性
| 名称 | 第10章 相交线、平行线和平移单元素养综合检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024沪科版数学七年级下册
第10章 相交线、平行线与平移
第10章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
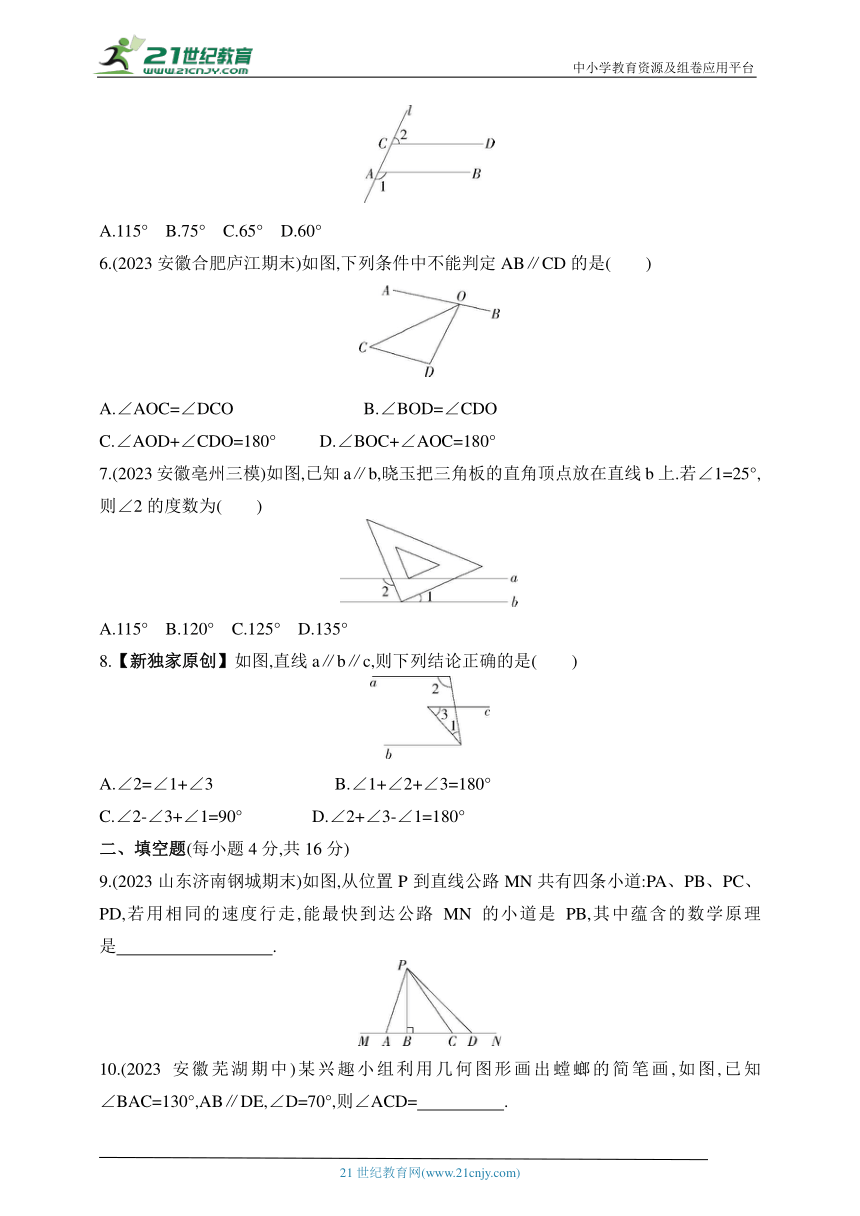
1.(2023黑龙江绥化期中)下面四个选项中,∠1与∠2是对顶角的是( )
A B
C D
2.(2023山东临沂中考)在同一平面内,过直线l外一点P作l的垂线m,再过点P作m的垂线n,则直线l与n的位置关系是( )
A.相交 B.相交且垂直 C.平行 D.不能确定
3.(2023安徽黄山期中)下列图形中,不能通过其中一个四边形平移得到的是( )
4.(2022安徽池州东至期末)如图,已知AC⊥BC,CD⊥AB于点D,可以表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
5.如图,将射线AB沿直线l平移得到射线CD,若∠1=115°,则∠2的度数是( )
A.115° B.75° C.65° D.60°
6.(2023安徽合肥庐江期末)如图,下列条件中不能判定AB∥CD的是( )
A.∠AOC=∠DCO B.∠BOD=∠CDO
C.∠AOD+∠CDO=180° D.∠BOC+∠AOC=180°
7.(2023安徽亳州三模)如图,已知a∥b,晓玉把三角板的直角顶点放在直线b上.若∠1=25°,则∠2的度数为( )
A.115° B.120° C.125° D.135°
8.【新独家原创】如图,直线a∥b∥c,则下列结论正确的是( )
A.∠2=∠1+∠3 B.∠1+∠2+∠3=180°
C.∠2-∠3+∠1=90° D.∠2+∠3-∠1=180°
二、填空题(每小题4分,共16分)
9.(2023山东济南钢城期末)如图,从位置P到直线公路MN共有四条小道:PA、PB、PC、PD,若用相同的速度行走,能最快到达公路MN的小道是PB,其中蕴含的数学原理是 .
10.(2023安徽芜湖期中)某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB∥DE,∠D=70°,则∠ACD= .
11.(2022江苏扬州高邮期末)如图,已知长方形ABCD的长为a,宽为b,若将长方形ABCD向右平移a,再向下平移b,得到长方形A'B'C'D',则阴影部分的面积为 .(用含a、b的代数式表示)
12.【新独家原创】如图,将一副三角板按如图所示的方式摆放在一起,直角顶点重合,其中∠ACD=∠BCE=90°,∠A=60°,∠D=30°,∠B=∠E=45°.
(1)当∠ACB=140°时,∠DCE的度数为 ;
(2)当∠ACE<135°,且点E在直线AC的上方时,若这两块三角板有两条边平行,则∠ACE的度数为 .
三、解答题(共60分)
13.(8分)如图,已知∠A=65°,∠1=∠C.
(1)写出∠1的同位角;
(2)求∠B的度数.
14.(2023安徽合肥庐江期中)(8分)在如图所示的网格中,每个小正方形的边长均为1,三角形ABC的顶点均在格点(网格线的交点)上.
(1)把三角形ABC向右平移5格,再向上平移3格得到三角形A'B'C',画出三角形A'B'C';
(2)求三角形A'B'C'的面积.
15.(2023辽宁沈阳皇姑期末)(10分)按逻辑将下面的证明过程补充完整.
已知:如图,∠BGE=∠CHF,∠1=∠2.
试证明:∠M=∠N.
证明:因为∠BGE+∠BGH=180°,∠CHF+∠CHG=180°,∠BGE=∠CHF,(已知)
所以∠BGH=∠CHG.( )
因为∠1=∠2,(已知)
所以∠BGH-∠1=∠CHG-∠2,
即 = ,
所以 ∥ ,( )
所以∠M=∠N.( )
16.【跨学科·物理】(2022河北石家庄栾城期中)(10分)如图1,潜望镜中的两面镜子是互相平行放置的,其示意图如图2所示,光线通过镜子反射时,∠1=∠2,∠3=∠4,且AB∥CD.
图1 图2
(1)猜想∠2和∠3有什么关系,并说明理由;
(2)求证:PM∥NQ.
17.(2023北京首师大附中月考)(12分)如图,直线AB、CD相交于点O,CD⊥OF,OE平分∠BOD.
(1)若∠AOC=70°,求∠EOF的度数;
(2)若∠EOF=α,请直接写出∠AOC的度数.(用含α的式子表示)
18.(2023广东汕头金平期末)(12分)如图,已知点G在EF上,点C,D在AB上,∠E=∠1,∠2=∠3.
(1)求证:AB∥EF;
(2)若CF⊥BG,∠4+∠B=90°,求证:AG∥CF;
(3)在(2)的条件下,若∠AGF=2∠F+30°,求∠5的度数.
第10章 相交线、平行线与平移
第10章 素养综合检测
1.C 一个角的两边分别是另一个角两边的反向延长线,则这两个角互为对顶角,故选项C正确.
2.C 同一平面内,垂直于同一条直线的两条直线平行,因为l⊥m,n⊥m,所以l∥n.
3.A 平移不改变图形的形状、大小以及图形的方向,故选项A中的图形不能由一个四边形平移得到.
4.C 因为AD⊥CD,所以点A到直线CD的距离是线段AD的长度.
5.C 因为AB∥CD,所以∠ACD=∠1=115°,所以∠2=180°-∠ACD=180°-115°=65°.
6.D 因为∠AOC=∠DCO,所以AB∥CD,故选项A不符合题意;因为∠BOD=∠CDO,所以AB∥CD,故选项B不符合题意;因为∠AOD+∠CDO=180°,所以AB∥CD,故选项C不符合题意;由∠BOC+∠AOC=180°,不能判定AB∥CD,故选项D符合题意.
7.A 如图,因为∠BAC=90°,∠1=25°,所以∠BAD=∠BAC+∠1=115°.因为a∥b,所以∠2=∠BAD=115°.
8.B 如图,因为b∥c,
所以∠3=∠4,
因为a∥b,
所以∠2+∠1+∠4=180°,
所以∠1+∠2+∠3=180°.
9. 答案 垂线段最短
解析 在连接直线外一点与直线上各点的线段中,垂线段最短.
10. 答案 20°
解析 过点C作CF∥AB,如图,
因为∠BAC=130°,
所以∠ACF=∠BAC=130°,
因为AB∥DE,
所以CF∥DE,
所以∠D+∠DCF=180°,
因为∠D=70°,
所以∠DCF=110°,
所以∠ACD=∠ACF-∠DCF=20°.
11. 答案 ab
解析 由题意得,题图中空白部分是长为a,宽为b的长方形,所以S阴影=2ab-2×a×b=ab.
12. 答案 (1)40° (2)30°或45°或120°
解析 (1)由题意可知∠ACE=∠ACB-∠BCE=50°,所以∠DCE=∠ACD-∠ACE=90°-50°=40°.
(2)因为∠ACE<135°,且点E在直线AC的上方,两块三角板有两条边平行,所以BE∥AC或BC∥AD或CE∥AD.
当BE∥AC时,∠ACE=∠E=45°;
当BC∥AD时,
因为∠A=60°,
所以∠ACB=120°,
因为∠BCE=90°,
所以∠ACE=120°-90°=30°;
当CE∥AD时,
因为∠D=30°,
所以∠DCE=∠D=30°,
所以∠ACE=∠ACD+∠DCE=90°+30°=120°.
综上所述,∠ACE的度数为30°或45°或120°.
13. 解析 (1)∠1的同位角是∠A.
(2)因为∠1=∠C,
所以AE∥BC,
所以∠A+∠B=180°.
因为∠A=65°,
所以∠B=180°-∠A=115°.
14. 解析 (1)如图所示,三角形A'B'C'即为所求.
(2)S三角形A'B'C'=3×3-×1×3-×1×2-×2×3=.
15. 证明 因为∠BGE+∠BGH=180°,∠CHF+∠CHG=180°,∠BGE=∠CHF,(已知)
所以∠BGH=∠CHG.(等角的补角相等)
因为∠1=∠2,(已知)
所以∠BGH-∠1=∠CHG-∠2,
即∠MGH=∠NHG,
所以MG∥NH,(内错角相等,两直线平行)
所以∠M=∠N.(两直线平行,内错角相等)
16. 解析 (1)∠2=∠3.
理由:因为AB∥CD,
所以∠2=∠3.
(2)证明:因为∠2=∠3,∠1=∠2,∠3=∠4,
所以∠1+∠2=∠3+∠4,
所以180°-(∠1+∠2)=180°-(∠3+∠4),
即∠5=∠6,所以PM∥NQ.
17. 解析 (1)因为CD⊥OF,
所以∠DOF=90°.
因为OE平分∠BOD,
所以∠DOE=∠BOD.
因为∠BOD=∠AOC=70°,
所以∠DOE=35°,
所以∠EOF=∠DOF-∠DOE=55°.
(2)∠AOC=180°-2α.
详解:因为OE平分∠BOD,
所以∠BOD=2∠DOE.
因为∠DOE=∠DOF-∠EOF=90°-α,
所以∠BOD=180°-2α,
所以∠AOC=∠BOD=180°-2α.
18. 解析 (1)证明:因为∠E=∠1,∠2=∠3,∠1=∠2,
所以∠E=∠3,
所以AB∥EF.
(2)证明:因为CF⊥BG,
所以∠CNB=90°,
所以∠B+∠BCN=90°.
因为∠4+∠B=90°,
所以∠4=∠BCN.
因为AB∥EF,
所以∠BCN=∠F,
所以∠4=∠F,
所以AG∥CF.
(3)因为AG∥CF,
所以∠AGF+∠F=180°.
因为∠AGF=2∠F+30°,
所以∠F=50°.
因为CF⊥BG,
所以∠FNG=90°,
所以∠5=90°-∠F=40°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版数学七年级下册
第10章 相交线、平行线与平移
第10章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023黑龙江绥化期中)下面四个选项中,∠1与∠2是对顶角的是( )
A B
C D
2.(2023山东临沂中考)在同一平面内,过直线l外一点P作l的垂线m,再过点P作m的垂线n,则直线l与n的位置关系是( )
A.相交 B.相交且垂直 C.平行 D.不能确定
3.(2023安徽黄山期中)下列图形中,不能通过其中一个四边形平移得到的是( )
4.(2022安徽池州东至期末)如图,已知AC⊥BC,CD⊥AB于点D,可以表示点A到直线CD的距离的是( )
A.线段CD的长度 B.线段AC的长度
C.线段AD的长度 D.线段BC的长度
5.如图,将射线AB沿直线l平移得到射线CD,若∠1=115°,则∠2的度数是( )
A.115° B.75° C.65° D.60°
6.(2023安徽合肥庐江期末)如图,下列条件中不能判定AB∥CD的是( )
A.∠AOC=∠DCO B.∠BOD=∠CDO
C.∠AOD+∠CDO=180° D.∠BOC+∠AOC=180°
7.(2023安徽亳州三模)如图,已知a∥b,晓玉把三角板的直角顶点放在直线b上.若∠1=25°,则∠2的度数为( )
A.115° B.120° C.125° D.135°
8.【新独家原创】如图,直线a∥b∥c,则下列结论正确的是( )
A.∠2=∠1+∠3 B.∠1+∠2+∠3=180°
C.∠2-∠3+∠1=90° D.∠2+∠3-∠1=180°
二、填空题(每小题4分,共16分)
9.(2023山东济南钢城期末)如图,从位置P到直线公路MN共有四条小道:PA、PB、PC、PD,若用相同的速度行走,能最快到达公路MN的小道是PB,其中蕴含的数学原理是 .
10.(2023安徽芜湖期中)某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB∥DE,∠D=70°,则∠ACD= .
11.(2022江苏扬州高邮期末)如图,已知长方形ABCD的长为a,宽为b,若将长方形ABCD向右平移a,再向下平移b,得到长方形A'B'C'D',则阴影部分的面积为 .(用含a、b的代数式表示)
12.【新独家原创】如图,将一副三角板按如图所示的方式摆放在一起,直角顶点重合,其中∠ACD=∠BCE=90°,∠A=60°,∠D=30°,∠B=∠E=45°.
(1)当∠ACB=140°时,∠DCE的度数为 ;
(2)当∠ACE<135°,且点E在直线AC的上方时,若这两块三角板有两条边平行,则∠ACE的度数为 .
三、解答题(共60分)
13.(8分)如图,已知∠A=65°,∠1=∠C.
(1)写出∠1的同位角;
(2)求∠B的度数.
14.(2023安徽合肥庐江期中)(8分)在如图所示的网格中,每个小正方形的边长均为1,三角形ABC的顶点均在格点(网格线的交点)上.
(1)把三角形ABC向右平移5格,再向上平移3格得到三角形A'B'C',画出三角形A'B'C';
(2)求三角形A'B'C'的面积.
15.(2023辽宁沈阳皇姑期末)(10分)按逻辑将下面的证明过程补充完整.
已知:如图,∠BGE=∠CHF,∠1=∠2.
试证明:∠M=∠N.
证明:因为∠BGE+∠BGH=180°,∠CHF+∠CHG=180°,∠BGE=∠CHF,(已知)
所以∠BGH=∠CHG.( )
因为∠1=∠2,(已知)
所以∠BGH-∠1=∠CHG-∠2,
即 = ,
所以 ∥ ,( )
所以∠M=∠N.( )
16.【跨学科·物理】(2022河北石家庄栾城期中)(10分)如图1,潜望镜中的两面镜子是互相平行放置的,其示意图如图2所示,光线通过镜子反射时,∠1=∠2,∠3=∠4,且AB∥CD.
图1 图2
(1)猜想∠2和∠3有什么关系,并说明理由;
(2)求证:PM∥NQ.
17.(2023北京首师大附中月考)(12分)如图,直线AB、CD相交于点O,CD⊥OF,OE平分∠BOD.
(1)若∠AOC=70°,求∠EOF的度数;
(2)若∠EOF=α,请直接写出∠AOC的度数.(用含α的式子表示)
18.(2023广东汕头金平期末)(12分)如图,已知点G在EF上,点C,D在AB上,∠E=∠1,∠2=∠3.
(1)求证:AB∥EF;
(2)若CF⊥BG,∠4+∠B=90°,求证:AG∥CF;
(3)在(2)的条件下,若∠AGF=2∠F+30°,求∠5的度数.
第10章 相交线、平行线与平移
第10章 素养综合检测
1.C 一个角的两边分别是另一个角两边的反向延长线,则这两个角互为对顶角,故选项C正确.
2.C 同一平面内,垂直于同一条直线的两条直线平行,因为l⊥m,n⊥m,所以l∥n.
3.A 平移不改变图形的形状、大小以及图形的方向,故选项A中的图形不能由一个四边形平移得到.
4.C 因为AD⊥CD,所以点A到直线CD的距离是线段AD的长度.
5.C 因为AB∥CD,所以∠ACD=∠1=115°,所以∠2=180°-∠ACD=180°-115°=65°.
6.D 因为∠AOC=∠DCO,所以AB∥CD,故选项A不符合题意;因为∠BOD=∠CDO,所以AB∥CD,故选项B不符合题意;因为∠AOD+∠CDO=180°,所以AB∥CD,故选项C不符合题意;由∠BOC+∠AOC=180°,不能判定AB∥CD,故选项D符合题意.
7.A 如图,因为∠BAC=90°,∠1=25°,所以∠BAD=∠BAC+∠1=115°.因为a∥b,所以∠2=∠BAD=115°.
8.B 如图,因为b∥c,
所以∠3=∠4,
因为a∥b,
所以∠2+∠1+∠4=180°,
所以∠1+∠2+∠3=180°.
9. 答案 垂线段最短
解析 在连接直线外一点与直线上各点的线段中,垂线段最短.
10. 答案 20°
解析 过点C作CF∥AB,如图,
因为∠BAC=130°,
所以∠ACF=∠BAC=130°,
因为AB∥DE,
所以CF∥DE,
所以∠D+∠DCF=180°,
因为∠D=70°,
所以∠DCF=110°,
所以∠ACD=∠ACF-∠DCF=20°.
11. 答案 ab
解析 由题意得,题图中空白部分是长为a,宽为b的长方形,所以S阴影=2ab-2×a×b=ab.
12. 答案 (1)40° (2)30°或45°或120°
解析 (1)由题意可知∠ACE=∠ACB-∠BCE=50°,所以∠DCE=∠ACD-∠ACE=90°-50°=40°.
(2)因为∠ACE<135°,且点E在直线AC的上方,两块三角板有两条边平行,所以BE∥AC或BC∥AD或CE∥AD.
当BE∥AC时,∠ACE=∠E=45°;
当BC∥AD时,
因为∠A=60°,
所以∠ACB=120°,
因为∠BCE=90°,
所以∠ACE=120°-90°=30°;
当CE∥AD时,
因为∠D=30°,
所以∠DCE=∠D=30°,
所以∠ACE=∠ACD+∠DCE=90°+30°=120°.
综上所述,∠ACE的度数为30°或45°或120°.
13. 解析 (1)∠1的同位角是∠A.
(2)因为∠1=∠C,
所以AE∥BC,
所以∠A+∠B=180°.
因为∠A=65°,
所以∠B=180°-∠A=115°.
14. 解析 (1)如图所示,三角形A'B'C'即为所求.
(2)S三角形A'B'C'=3×3-×1×3-×1×2-×2×3=.
15. 证明 因为∠BGE+∠BGH=180°,∠CHF+∠CHG=180°,∠BGE=∠CHF,(已知)
所以∠BGH=∠CHG.(等角的补角相等)
因为∠1=∠2,(已知)
所以∠BGH-∠1=∠CHG-∠2,
即∠MGH=∠NHG,
所以MG∥NH,(内错角相等,两直线平行)
所以∠M=∠N.(两直线平行,内错角相等)
16. 解析 (1)∠2=∠3.
理由:因为AB∥CD,
所以∠2=∠3.
(2)证明:因为∠2=∠3,∠1=∠2,∠3=∠4,
所以∠1+∠2=∠3+∠4,
所以180°-(∠1+∠2)=180°-(∠3+∠4),
即∠5=∠6,所以PM∥NQ.
17. 解析 (1)因为CD⊥OF,
所以∠DOF=90°.
因为OE平分∠BOD,
所以∠DOE=∠BOD.
因为∠BOD=∠AOC=70°,
所以∠DOE=35°,
所以∠EOF=∠DOF-∠DOE=55°.
(2)∠AOC=180°-2α.
详解:因为OE平分∠BOD,
所以∠BOD=2∠DOE.
因为∠DOE=∠DOF-∠EOF=90°-α,
所以∠BOD=180°-2α,
所以∠AOC=∠BOD=180°-2α.
18. 解析 (1)证明:因为∠E=∠1,∠2=∠3,∠1=∠2,
所以∠E=∠3,
所以AB∥EF.
(2)证明:因为CF⊥BG,
所以∠CNB=90°,
所以∠B+∠BCN=90°.
因为∠4+∠B=90°,
所以∠4=∠BCN.
因为AB∥EF,
所以∠BCN=∠F,
所以∠4=∠F,
所以AG∥CF.
(3)因为AG∥CF,
所以∠AGF+∠F=180°.
因为∠AGF=2∠F+30°,
所以∠F=50°.
因为CF⊥BG,
所以∠FNG=90°,
所以∠5=90°-∠F=40°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
