第7章 一次方程组单元素养综合检测试题(含解析)
文档属性
| 名称 | 第7章 一次方程组单元素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 386.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学七年级下册
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023吉林白山抚松期中)若方程组是二元一次方程组,则“……”可以是( )
A.x=2y B.xy=1
C.=2 D.x2=1
2.(2023四川成都金牛期末)若是关于x和y的二元一次方程2x-ay=6的解,则a的值是( )
A.-2 B.2 C.-4 D.4
3.(2023湖北襄阳樊城期末)用代入消元法解方程组下列变形不正确的是( )
A.由②得x=
B.由②得y=
C.由①得x=
D.由①得y=5-2x
4.(2023湖北恩施州恩施市期末)解方程组的思路可用如图所示的框图表示,圈中应填写的对方程①,②所做的变形为( )
A.①×2+②×3 B.①×2-②×3
C.①×3-②×2 D.①×3+②×2
5.(2023四川巴中恩阳期中)解关于x、y的二元一次方程组用代入消元法消去y后所得到的方程为( )
A.2x-x+3=5 B.2x+x-3=5
C.2x+x+3=5 D.2x-x-3=5
6.(2023河南洛阳宜阳期中)方程组的解为( )
A.
C.
7.(2022湖南株洲荷塘景炎中学期中)已知代数式ax2+bx+c,当x=-1时,其值为4;当x=1时,其值为8;当x=2时,其值为25,则当x=3时,其值为( )
A.4 B.8
C.62 D.52
8.【新独家原创】已知解关于x、y的二元一次方程组时,①+②可以消去y,①-②可以消去x,则a-b的值为( )
A.-1 B.1
C.5 D.-5
9.(2023湖南永州双牌期末)已知关于x、y的方程组有相同的解,则a和b的值分别为( )
A.2,-3 B.4,-6
C.-2,3 D.-4,6
10.【数学文化】(2023四川成都金牛模拟)古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何 若设乌鸦有x只,树有y棵,则由题意可列方程组( )
A.
C.
二、填空题(每小题3分,共18分)
11.(2023福建泉州德化期中)若方程5xk-1+2y=-1是关于x、y的二元一次方程,则k= .
12.(2023四川巴中恩阳模拟)方程组的解为 .
13.(2023浙江温州文成期中)已知方程组若x+y=5,则m的值为 .
14.(2023福建厦门思明湖滨中学期中)如果的解,那么代数式a+b的值为 .
15.【新独家原创】对于有理数x、y定义一种新的运算:x#y=ax+2by,其中a,b为常数,已知2#1=5,3#2=8,则a-b= .
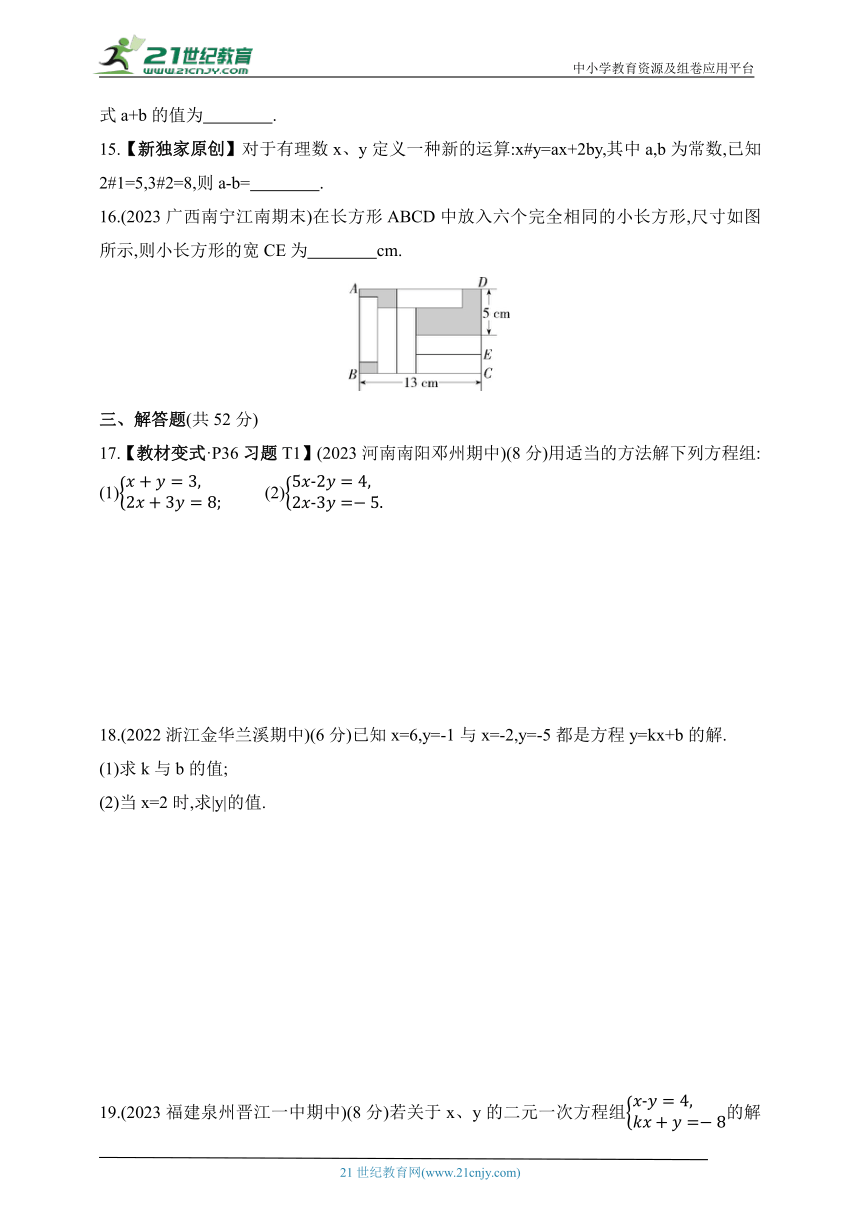
16.(2023广西南宁江南期末)在长方形ABCD中放入六个完全相同的小长方形,尺寸如图所示,则小长方形的宽CE为 cm.
三、解答题(共52分)
17.【教材变式·P36习题T1】(2023河南南阳邓州期中)(8分)用适当的方法解下列方程组:
(1) (2)
18.(2022浙江金华兰溪期中)(6分)已知x=6,y=-1与x=-2,y=-5都是方程y=kx+b的解.
(1)求k与b的值;
(2)当x=2时,求|y|的值.
19.(2023福建泉州晋江一中期中)(8分)若关于x、y的二元一次方程组的解满足x、y互为相反数,求k的值.
20.【新素材】(2023吉林松原乾安模拟)(10分)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知1片银杏树叶一年的平均滞尘量比1片国槐树叶一年的平均滞尘量的2倍少4毫克,若2片国槐树叶与1片银杏树叶一年的平均滞尘总量为84毫克.请分别求出1片国槐树叶和1片银杏树叶一年的平均滞尘量.
21.【新考向·规律探究题】(10分)下图是按一定规律排列的方程组的集合和其解的集合的对应关系图,方程组从左至右依次记为方程组1、方程组2、方程组3、……、方程组n.
(1)将方程组1的解填入图中;
(2)请依据方程组和其解的变化规律,将方程组n和它的解直接填入图中;
(3)若方程组求a的值,并判断该方程组是否符合(2)中的规律.
22.(2023福建泉州一中期中)(10分)用如图1所示的A、B两种纸板作侧面或底面制作如图2所示的甲、乙两种长方体形状的无盖纸盒.
(1)现有A型纸板70张,B型纸板160张,要求恰好用完所有纸板,问可制作甲、乙两种无盖纸盒各多少个
(2)若仓库A型纸板较为充足,B型纸板只有30张,根据现有的纸板最多可以制作多少个如图2所示的无盖纸盒(甲、乙两种都有,要求B型纸板用完)
(3)经测量发现B型纸板的长是宽的2倍(即b=2a),若仓库有6个如图3所示的丙型无盖大纸盒(长、宽、高分别为2a、a、2a),现将6个丙型无盖大纸盒经过拆剪制作成甲、乙两种型号的纸盒,可以各做多少个(假设没有边角消耗,没有余料)
图1 图2 图3
答案全解全析
1.A A.x=2y与x+y=2能组成二元一次方程组,故该选项符合题意;B.xy=1中含未知数的项的次数为2,与x+y=2不能组成二元一次方程组,故该选项不符合题意;C.不是整式,故该选项不符合题意;D.x2=1中含未知数的项的次数为2,与x+y=2不能组成二元一次方程组,故该选项不符合题意.故选A.
2.B 把代入方程2x-ay=6得10-2a=6,解得a=2,故选B.
3.C A.由②得3x=2-4y,∴x=,故本选项不符合题意;B.由②得4y=2-3x,∴y=,故本选项不符合题意;C.由①得2x=5-y,∴x=,故本选项符合题意;D.由①得y=5-2x,故本选项不符合题意.故选C.
4.C ①×3得6x+9y=24③,②×2得6x-4y=-2④,③-④得(6x+9y)-(6x-4y)=24-(-2),即变形的思路是①×3-②×2,故选C.
5.D 将①代入②得2x-(x+3)=5,去括号得2x-x-3=5.故选D.
6.A ②-①×2得y=2,把y=2代入①得x+2=5,解得x=3,∴方程组的解为故选A.
7.D 由题意得①+②可得a+c=6④,①×2+③可得2a+c=11⑤,⑤-④得a=5,把a=5代入④得5+c=6,解得c=1,把a=5,c=1代入①得5-b+1=4,解得b=2,∴ax2+bx+c=5x2+2x+1,∴当x=3时,ax2+bx+c=5×32+2×3+1=45+6+1=52.故选D.
8.C 根据题意得b=-2,a=3,所以a-b=3-(-2)=5.故选C.
9.C 解方程组故选C.
10.D 依题意得故选D.
11.2
解析 ∵方程5xk-1+2y=-1是关于x、y的二元一次方程,∴k-1=1,解得k=2.
12.
解析 ①×2+②得7x=4,解得x=,把x=代入①得-y=3,解得y=-,∴方程组的解为
13.3
解析 ①-②得x+y=2m-1,∵x+y=5,∴2m-1=5,解得m=3.
14.1
解析 把即a+b=1.
15.
解析 ∵2#1=5,3#2=8,∴2a+2b=5,3a+4b=8,联立∴a-b=2-.
16.2
解析 设小长方形的长为x cm,宽为y cm,则AD=(x+3y)cm,AB=x+y=(5+2y)cm,即x-y=5,根据题意得即CE=2 cm.
17.解析 (1)①×2-②得-y=-2,解得y=2,将y=2代入①得x+2=3,解得x=1,∴原方程组的解为
(2)①×3-②×2得11x=22,解得x=2,将x=2代入①得10-2y=4,解得y=3,∴原方程组的解为
18.解析 (1)根据题意可得
(2)由(1)可得y=x-4,将x=2代入得y=-3,
∴|y|=3.
19.解析 依题意得代入kx+y=-8,得2k-2=-8,解得k=-3.
20.解析 设1片国槐树叶一年的平均滞尘量为x毫克,1片银杏树叶一年的平均滞尘量为y毫克,
由题意得
答:1片国槐树叶一年的平均滞尘量为22毫克,1片银杏树叶一年的平均滞尘量为40毫克.
21.解析 (1)解方程组
(2)易知每一个方程组中第1个方程相同,
每一个方程组的第2个方程中,y的系数依次为-1,-2,-3,…,-n,等号右面的数依次为1,4,9,…,n2,
每一个方程组的解中,相应x的值依次为1,2,3,…,n,相应y的值依次为0,-1,-2,…,-(n-1),
所以方程组n是
它的解为
(3)因为的解,
所以5-a×(-4)=25,解得a=5,
即原方程组为
所以该方程组符合(2)中的规律.
22.解析 (1)设可制作甲型无盖纸盒x个,乙型无盖纸盒y个,
则由题意得
答:可制作甲型无盖纸盒24个,乙型无盖纸盒22个.
(2)设制作甲型无盖纸盒m个,乙型无盖纸盒k个,共用n张A型纸板,
则由题意可得
消去k得m=n-6,
∵m,n为正整数,k≠0,
∴可得
综上,最多可以制作甲、乙两种无盖纸盒共9个.
(3)因为1个丙型大纸盒可以拆成7张B型纸板,所以6个丙型大纸盒可以拆成42张B型纸板.制作1个甲型无盖纸盒需要4张B型纸板,制作1个乙型无盖纸盒需要4.5张B型纸板.
设制作甲型无盖纸盒c个,乙型无盖纸盒d个,则4c+4.5d=42,因为c,d为正整数,所以c=6,d=4.
答:可以制作甲型无盖纸盒6个,乙型无盖纸盒4个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学七年级下册
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023吉林白山抚松期中)若方程组是二元一次方程组,则“……”可以是( )
A.x=2y B.xy=1
C.=2 D.x2=1
2.(2023四川成都金牛期末)若是关于x和y的二元一次方程2x-ay=6的解,则a的值是( )
A.-2 B.2 C.-4 D.4
3.(2023湖北襄阳樊城期末)用代入消元法解方程组下列变形不正确的是( )
A.由②得x=
B.由②得y=
C.由①得x=
D.由①得y=5-2x
4.(2023湖北恩施州恩施市期末)解方程组的思路可用如图所示的框图表示,圈中应填写的对方程①,②所做的变形为( )
A.①×2+②×3 B.①×2-②×3
C.①×3-②×2 D.①×3+②×2
5.(2023四川巴中恩阳期中)解关于x、y的二元一次方程组用代入消元法消去y后所得到的方程为( )
A.2x-x+3=5 B.2x+x-3=5
C.2x+x+3=5 D.2x-x-3=5
6.(2023河南洛阳宜阳期中)方程组的解为( )
A.
C.
7.(2022湖南株洲荷塘景炎中学期中)已知代数式ax2+bx+c,当x=-1时,其值为4;当x=1时,其值为8;当x=2时,其值为25,则当x=3时,其值为( )
A.4 B.8
C.62 D.52
8.【新独家原创】已知解关于x、y的二元一次方程组时,①+②可以消去y,①-②可以消去x,则a-b的值为( )
A.-1 B.1
C.5 D.-5
9.(2023湖南永州双牌期末)已知关于x、y的方程组有相同的解,则a和b的值分别为( )
A.2,-3 B.4,-6
C.-2,3 D.-4,6
10.【数学文化】(2023四川成都金牛模拟)古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.请你动脑筋,鸦树各几何 若设乌鸦有x只,树有y棵,则由题意可列方程组( )
A.
C.
二、填空题(每小题3分,共18分)
11.(2023福建泉州德化期中)若方程5xk-1+2y=-1是关于x、y的二元一次方程,则k= .
12.(2023四川巴中恩阳模拟)方程组的解为 .
13.(2023浙江温州文成期中)已知方程组若x+y=5,则m的值为 .
14.(2023福建厦门思明湖滨中学期中)如果的解,那么代数式a+b的值为 .
15.【新独家原创】对于有理数x、y定义一种新的运算:x#y=ax+2by,其中a,b为常数,已知2#1=5,3#2=8,则a-b= .
16.(2023广西南宁江南期末)在长方形ABCD中放入六个完全相同的小长方形,尺寸如图所示,则小长方形的宽CE为 cm.
三、解答题(共52分)
17.【教材变式·P36习题T1】(2023河南南阳邓州期中)(8分)用适当的方法解下列方程组:
(1) (2)
18.(2022浙江金华兰溪期中)(6分)已知x=6,y=-1与x=-2,y=-5都是方程y=kx+b的解.
(1)求k与b的值;
(2)当x=2时,求|y|的值.
19.(2023福建泉州晋江一中期中)(8分)若关于x、y的二元一次方程组的解满足x、y互为相反数,求k的值.
20.【新素材】(2023吉林松原乾安模拟)(10分)科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知1片银杏树叶一年的平均滞尘量比1片国槐树叶一年的平均滞尘量的2倍少4毫克,若2片国槐树叶与1片银杏树叶一年的平均滞尘总量为84毫克.请分别求出1片国槐树叶和1片银杏树叶一年的平均滞尘量.
21.【新考向·规律探究题】(10分)下图是按一定规律排列的方程组的集合和其解的集合的对应关系图,方程组从左至右依次记为方程组1、方程组2、方程组3、……、方程组n.
(1)将方程组1的解填入图中;
(2)请依据方程组和其解的变化规律,将方程组n和它的解直接填入图中;
(3)若方程组求a的值,并判断该方程组是否符合(2)中的规律.
22.(2023福建泉州一中期中)(10分)用如图1所示的A、B两种纸板作侧面或底面制作如图2所示的甲、乙两种长方体形状的无盖纸盒.
(1)现有A型纸板70张,B型纸板160张,要求恰好用完所有纸板,问可制作甲、乙两种无盖纸盒各多少个
(2)若仓库A型纸板较为充足,B型纸板只有30张,根据现有的纸板最多可以制作多少个如图2所示的无盖纸盒(甲、乙两种都有,要求B型纸板用完)
(3)经测量发现B型纸板的长是宽的2倍(即b=2a),若仓库有6个如图3所示的丙型无盖大纸盒(长、宽、高分别为2a、a、2a),现将6个丙型无盖大纸盒经过拆剪制作成甲、乙两种型号的纸盒,可以各做多少个(假设没有边角消耗,没有余料)
图1 图2 图3
答案全解全析
1.A A.x=2y与x+y=2能组成二元一次方程组,故该选项符合题意;B.xy=1中含未知数的项的次数为2,与x+y=2不能组成二元一次方程组,故该选项不符合题意;C.不是整式,故该选项不符合题意;D.x2=1中含未知数的项的次数为2,与x+y=2不能组成二元一次方程组,故该选项不符合题意.故选A.
2.B 把代入方程2x-ay=6得10-2a=6,解得a=2,故选B.
3.C A.由②得3x=2-4y,∴x=,故本选项不符合题意;B.由②得4y=2-3x,∴y=,故本选项不符合题意;C.由①得2x=5-y,∴x=,故本选项符合题意;D.由①得y=5-2x,故本选项不符合题意.故选C.
4.C ①×3得6x+9y=24③,②×2得6x-4y=-2④,③-④得(6x+9y)-(6x-4y)=24-(-2),即变形的思路是①×3-②×2,故选C.
5.D 将①代入②得2x-(x+3)=5,去括号得2x-x-3=5.故选D.
6.A ②-①×2得y=2,把y=2代入①得x+2=5,解得x=3,∴方程组的解为故选A.
7.D 由题意得①+②可得a+c=6④,①×2+③可得2a+c=11⑤,⑤-④得a=5,把a=5代入④得5+c=6,解得c=1,把a=5,c=1代入①得5-b+1=4,解得b=2,∴ax2+bx+c=5x2+2x+1,∴当x=3时,ax2+bx+c=5×32+2×3+1=45+6+1=52.故选D.
8.C 根据题意得b=-2,a=3,所以a-b=3-(-2)=5.故选C.
9.C 解方程组故选C.
10.D 依题意得故选D.
11.2
解析 ∵方程5xk-1+2y=-1是关于x、y的二元一次方程,∴k-1=1,解得k=2.
12.
解析 ①×2+②得7x=4,解得x=,把x=代入①得-y=3,解得y=-,∴方程组的解为
13.3
解析 ①-②得x+y=2m-1,∵x+y=5,∴2m-1=5,解得m=3.
14.1
解析 把即a+b=1.
15.
解析 ∵2#1=5,3#2=8,∴2a+2b=5,3a+4b=8,联立∴a-b=2-.
16.2
解析 设小长方形的长为x cm,宽为y cm,则AD=(x+3y)cm,AB=x+y=(5+2y)cm,即x-y=5,根据题意得即CE=2 cm.
17.解析 (1)①×2-②得-y=-2,解得y=2,将y=2代入①得x+2=3,解得x=1,∴原方程组的解为
(2)①×3-②×2得11x=22,解得x=2,将x=2代入①得10-2y=4,解得y=3,∴原方程组的解为
18.解析 (1)根据题意可得
(2)由(1)可得y=x-4,将x=2代入得y=-3,
∴|y|=3.
19.解析 依题意得代入kx+y=-8,得2k-2=-8,解得k=-3.
20.解析 设1片国槐树叶一年的平均滞尘量为x毫克,1片银杏树叶一年的平均滞尘量为y毫克,
由题意得
答:1片国槐树叶一年的平均滞尘量为22毫克,1片银杏树叶一年的平均滞尘量为40毫克.
21.解析 (1)解方程组
(2)易知每一个方程组中第1个方程相同,
每一个方程组的第2个方程中,y的系数依次为-1,-2,-3,…,-n,等号右面的数依次为1,4,9,…,n2,
每一个方程组的解中,相应x的值依次为1,2,3,…,n,相应y的值依次为0,-1,-2,…,-(n-1),
所以方程组n是
它的解为
(3)因为的解,
所以5-a×(-4)=25,解得a=5,
即原方程组为
所以该方程组符合(2)中的规律.
22.解析 (1)设可制作甲型无盖纸盒x个,乙型无盖纸盒y个,
则由题意得
答:可制作甲型无盖纸盒24个,乙型无盖纸盒22个.
(2)设制作甲型无盖纸盒m个,乙型无盖纸盒k个,共用n张A型纸板,
则由题意可得
消去k得m=n-6,
∵m,n为正整数,k≠0,
∴可得
综上,最多可以制作甲、乙两种无盖纸盒共9个.
(3)因为1个丙型大纸盒可以拆成7张B型纸板,所以6个丙型大纸盒可以拆成42张B型纸板.制作1个甲型无盖纸盒需要4张B型纸板,制作1个乙型无盖纸盒需要4.5张B型纸板.
设制作甲型无盖纸盒c个,乙型无盖纸盒d个,则4c+4.5d=42,因为c,d为正整数,所以c=6,d=4.
答:可以制作甲型无盖纸盒6个,乙型无盖纸盒4个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
