第9章 多边形单元素养综合检测试题(含解析)
文档属性
| 名称 | 第9章 多边形单元素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 632.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024华东师大版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023湖南衡阳中考)下列长度的各组线段能组成一个三角形的是( )
A.1 cm,2 cm,3 cm B.3 cm,8 cm,5 cm
C.4 cm,5 cm,10 cm D.4 cm,5 cm,6 cm
2.(2023福建三明三元期中)下列各三角形中,正确画出△ABC的AC边上的高的是( )
A B C D
3.【新考法】(2023河南周口太康期末)将一副三角板按如图所示的方式摆放,其中有两边互相垂直,则∠1=( )
A.45° B.50° C.60° D.75°
4.(2023河南南阳西峡期末)下列正多边形组合不能铺满地面的是( )
A.正三角形与正方形
B.正方形与正六边形
C.正方形与正八边形
D.正三角形,正方形与正六边形
5.(2023福建南平政和模拟)具备下列条件的△ABC不是直角三角形的是( )
A.∠A=∠B=3∠C
B.∠A+∠B=∠C
C.∠A=∠B=∠C
D.∠A∶∠B∶∠C=1∶2∶3
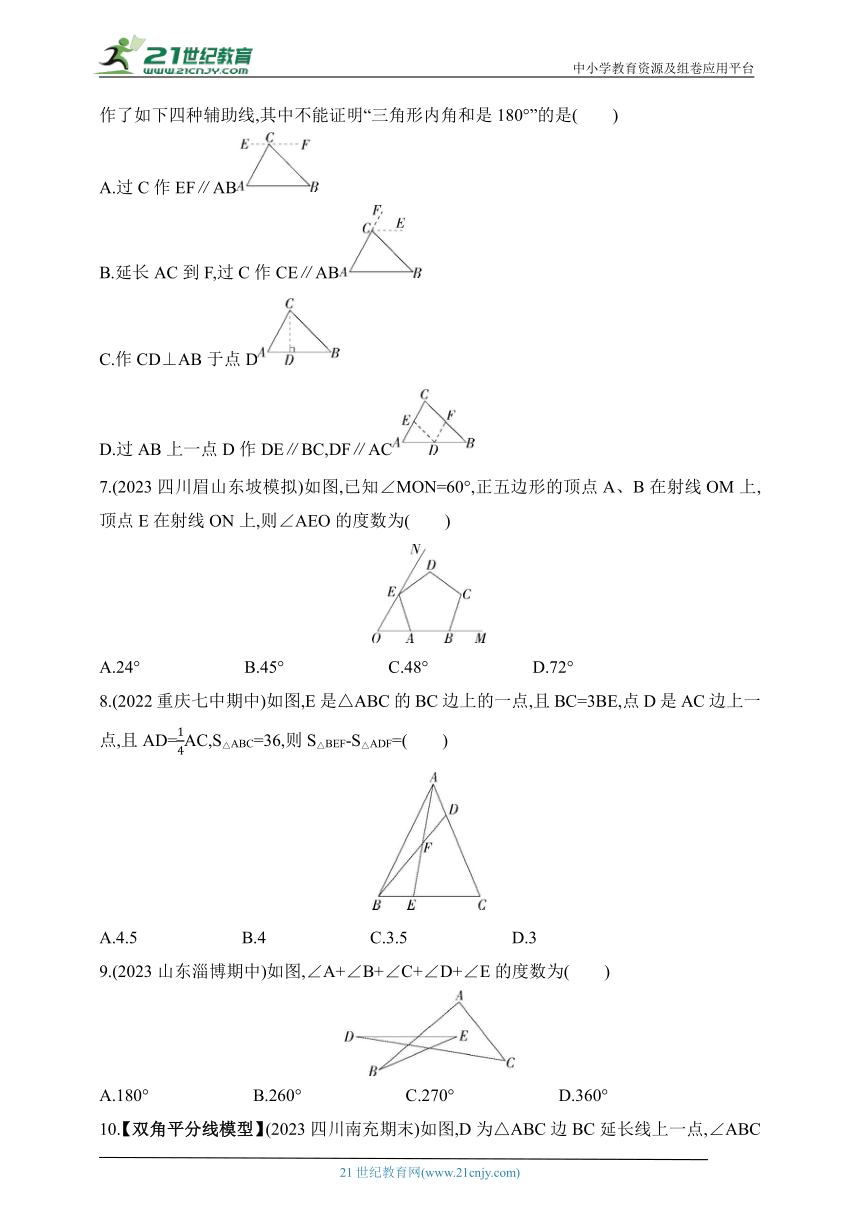
6.(2023河南信阳淮滨期中)在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )
A.过C作EF∥AB
B.延长AC到F,过C作CE∥AB
C.作CD⊥AB于点D
D.过AB上一点D作DE∥BC,DF∥AC
7.(2023四川眉山东坡模拟)如图,已知∠MON=60°,正五边形的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO的度数为( )
A.24° B.45° C.48° D.72°
8.(2022重庆七中期中)如图,E是△ABC的BC边上的一点,且BC=3BE,点D是AC边上一点,且AD=AC,S△ABC=36,则S△BEF-S△ADF=( )
A.4.5 B.4 C.3.5 D.3
9.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260° C.270° D.360°
10.【双角平分线模型】(2023四川南充期末)如图,D为△ABC边BC延长线上一点,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线交于点A2,……,∠A2 022BC与∠A2 022CD的平分线交于点A2 023,若∠A2 023=α,则∠A=( )
A.2 022α B.2 023α C.22 022α D.22 023α
二、填空题(每小题3分,共18分)
11.(2023吉林中考)如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
12.(2023福建龙岩模拟)若三角形的三边的长都是整数,其中两边长分别为2和5,则第三边的长可以是 .(只需写出一个符合条件的整数)
13.【新独家原创】如图,五边形ABCDE中,BC∥DE,则x的值为 .
14.(2023河南鹤壁期末)如图,在△ABC中,AD是∠BAC的平分线,EG∥AD,交BC于E、AB于F、CA的延长线于G,∠B=30°,∠C=70°,则∠G的度数为 °
15.(2023四川成都四十三中期中)如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点,且S△ABC=15 cm2,则图中△CEF的面积= .
16.(2023四川成都青羊树德实验中学期中)我们定义:在一个三角形中,若一个内角的度数是另一个内角度数的7倍,则这样的三角形被称为“德馨三角形”.如:三个内角分别为100°,70°,10°的三角形是“德馨三角形”.如图,点E在△ABC的边AC上,连结BE,作∠AEB的平分线交AB于点D,在BE上取点F,使∠BFD+∠BEC=180°,∠EDF=∠C.若△BCE是“德馨三角形”,则∠C的度数为 .
三、解答题(共52分)
17.(2023福建福州鼓楼延安中学期末)(6分)如图,在△ABC中,AD是BC边上的高,BE平分∠ABC.若∠ABC=70°,∠DAC=50°,求∠AEB的度数.
18.(2022广东云浮期末)(8分)若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边长均为整数,求△ABC的周长.
19.(2022湖南邵阳武冈期中)(8分)如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
20.(2023山西太原二模)(8分)如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;方法二:延长BC交AD于点E;方法三:连结BD.
请选择上述一种方法,求∠BCD的度数.
21.【双角平分线模型】(2023天津东丽期末)(10分)如图1,BE平分∠ABC,且与△ABC的外角∠ACD的平分线交于点E.
(1)若∠ABC=80°,∠ACB=50°,求∠E的度数;
(2)若把∠A截去,得到四边形MBCN,如图2,猜想∠E,∠M,∠N的数量关系并证明.
图1 图2
22.(2023山东日照东港泰安路中学期末)(12分)如图,多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当BM∥DN时,∠A和∠C满足什么数量关系,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
图1 图2
图3
答案全解全析
1.D A.∵1+2=3,∴长度为1 cm,2 cm,3 cm的三条线段不能组成三角形,本选项不符合题意;B.∵3+5=8,∴长度为3 cm,8 cm,5 cm的三条线段不能组成三角形,本选项不符合题意;C.∵4+5<10,∴长度为4 cm,5 cm,10 cm的三条线段不能组成三角形,本选项不符合题意;D.∵4+5>6,∴长度为4 cm,5 cm,6 cm的三条线段能组成三角形,本选项符合题意.故选D.
2.D 过点B作AC所在直线的垂线段,该垂线段即为△ABC的AC边上的高,∴四个选项中只有选项D符合题意.故选D.
3.D 本题以一副三角板组合图为背景,考查对三角形外角的性质的理解与把握.如图,由题意可知,∠2=45°,∠4=30°,
∴∠3=90°-∠2=45°,∴∠1=∠3+∠4=45°+30°=75°,故选D.
4.B A.正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面;B.正方形的每个内角是90°,正六边形的每个内角是120°,令90m+120n=360,得m=4-n,显然n取任何正整数时,m都不能得正整数,故不能铺满;C.正方形的每个内角是90°,正八边形的每个内角是135°,∵90°+2×135°=360°,∴能铺满地面;D.正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120°,∵60°+2×90°+120°=360°,∴能铺满地面.故选B.
5.A A.由∠A=∠B=3∠C及∠A+∠B+∠C=180°可得∠A=∠B=,∠C=,△ABC不是直角三角形,故符合题意;B.由∠A+∠B=∠C及∠A+∠B+∠C=180°可得∠C=90°,△ABC是直角三角形,故不符合题意;C.由∠A=∠B=∠C及∠A+∠B+∠C=180°可得∠C=90°,∠A=∠B=45°,△ABC是直角三角形,故不符合题意;D.由∠A∶∠B∶∠C=1∶2∶3及∠A+∠B+∠C=180°可得∠C=90°,∠A=30°,∠B=60°,△ABC是直角三角形,故不符合题意.故选A.
6.C A.由EF∥AB,得∠ECA=∠A,∠FCB=∠B.由∠ECA+∠ACB+∠FCB=180°,得∠A+∠ACB+∠B=180°,故A不符合题意.B.由CE∥AB,得∠A=∠FCE,∠B=∠BCE.由∠FCE+∠ECB+∠ACB=180°,得∠A+∠B+∠ACB=180°,故B不符合题意.C.由CD⊥AB于D,得∠ADC=∠CDB=90°,无法证得三角形内角和是180°,故C符合题意.D.由DF∥AC,得∠EDF=∠AED,∠A=∠FDB.由ED∥CB,得∠EDA=∠B,∠C=∠AED,那么∠C=∠EDF.由∠ADE+∠EDF+∠FDB=180°,得∠B+∠C+∠A=180°,故D不符合题意.故选C.
7.C ∵五边形ABCDE为正五边形,∴∠BAE=(5-2)×180°÷5=108°,∵∠MON=60°,∴∠AEO=∠BAE-
∠MON=108°-60°=48°,故选C.
8.D ∵BC=3BE,AD=AC,S△ABC=36,∴S△ABE=S△ABC=×36=12,S△ABD=S△ABC=9,∴S△BEF-S△ADF=S△ABE-S△ABD=12-9=3,故选D.
9.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+∠D+∠E+∠C=180°,故选A.
10.D 在△ABC中,∠A=∠ACD-∠ABC,∵∠ABC的平分线与∠ACD的平分线交于点A1,∴∠A1=∠A1CD-∠A1BC=(∠ACD-∠ABC)=∠A,同理可得∠A2=∠A1=∠A,∠A3=∠A2=∠A,……,
∠An=∠A,∵∠A2 023=α,∴∠A=α,即∠A=22 023α.故选D.
11.三角形具有稳定性
12.4(答案不唯一)
解析 设第三边长为x,∵三角形的两边长分别为2和5,∴5-213.130
解析 ∵BC∥DE,∴∠C+∠D=180°,∵∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,∴x+x+10+x-40+180=540,解得x=130.故答案为130.
14.40
解析 ∵∠B=30°,∠C=70°,∴∠BAC=180°-∠B-∠C=80°.∵AD平分∠BAC,∴∠DAC=∠BAC=40°.∵EG∥AD,∴∠G=
∠DAC=40°.故答案为40.
15. cm2
解析 ∵点D,E,F分别为BC,AD,BE的中点,∴S△ABD=2S△BDE,S△ADC=2S△CDE,S△EBC=2S△CEF,∵S△ABC=S△ABD+S△ADC,S△ECB=S△BDE+S△CDE,∴S△ABC=2S△BCE,∴S△ABC=4S△CEF,∵S△ABC=15 cm2,∴S△CEF=×15=(cm2),故答案为 cm2.
16.20°或84°
解析 ∵∠BFD+∠BEC=180°,∠BEC+∠AEB=180°,∴∠BFD=∠AEB,∴AC∥DF,∴∠AED=∠EDF,∵∠EDF=∠C,∴∠C=∠AED,∴DE∥BC,∴∠BED=∠CBE,∵ED平分∠AEB,∴∠AED=∠BED,∴∠C=∠CBE.∵△BCE是“德馨三角形”,∴当7∠C=∠BEC时,∠C+∠C+7∠C=180°,解得∠C=20°;当7∠BEC=∠C时,∠C+∠C+∠C=180°,解得∠C=84°.故答案为20°或84°.
17.解析 ∵AD是BC边上的高,∴∠ADC=90°,在Rt△ACD中,∠C=90°-∠DAC=90°-50°=40°,∵BE平分∠ABC,∴∠EBC=∠ABC=×70°=35°,∴∠AEB=∠EBC+∠C=35°+40°=75°.
18.解析 (1)根据三角形的三边关系,得
解得3(2)因为△ABC的三边长均为整数,且319.解析 如图,由三角形内角和定理得∠1+∠5=∠8+∠9,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠5+∠2+∠3+∠4+∠6+∠7=∠8+∠9+∠2+∠3+∠4+∠6+∠7=180°×(5-2)=540°.
20.解析 方法一:作射线AC,如图,由三角形外角的性质,得∠1=∠B+∠3,∠2=∠4+∠D,
所以∠1+∠2=∠B+∠3+∠4+∠D=∠B+∠D+∠BAD=55°+20°+45°=120°.
方法二:延长BC交AD于点E,如图,
∵∠CED=∠A+∠B,∠BCD=∠CED+∠D,
∴∠BCD=∠A+∠B+∠D=45°+55°+20°=120°.
方法三:连结BD,如图.
由三角形内角和定理,得∠A+∠ABD+∠ADB=180°,因为∠A=45°,∠ABC=55°,∠ADC=20°,所以∠CBD+∠CDB=180°-(45°+55°+20°)=60°,在△BDC中,由三角形内角和定理,得∠BCD=180°-60°=120°.
21.解析 (1)∵BE平分∠ABC,CE平分∠ACD,
∴∠EBC=∠ABC,∠ECD=∠ACD,
∵∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC,
∴∠ACD=∠E+∠EBC,
∴(∠A+∠ABC)=∠E+∠EBC,∴∠A+∠ABC=∠E+∠EBC,∴∠A=∠E,
∵∠A=180°-∠ABC-∠ACB,∠ABC=80°,∠ACB=50°,∴∠A=50°,∴∠E=25°.
(2)∠E=(∠BMN+∠MNC-180°).证明:分别延长BM和CN相交于点A,如图,∵∠A+∠AMN+∠ANM=180°,∠AMN+∠BMN=180°,∠ANM+∠MNC=180°,∴∠A=180°-(∠AMN+∠ANM)=180°-(180°-∠BMN+180°-∠MNC)=∠BMN+∠MNC-180°,
又由(1)知∠E=∠A,∴∠E=(∠BMN+∠MNC-180°).
22.解析 (1)①∵∠A=50°,∠C=100°,∴在四边形ABCD中,∠ABC+∠ADC=360°-∠A-∠C=210°,∴∠CBE+∠CDF=150°.∵∠CBE和∠CDF的平分线分别为BM,DN,∴∠PBC+∠PDC=∠CBE+∠CDF=(∠CBE+∠CDF)=×150°=75°,
∴∠BPD=360°-∠A-(∠ABC+∠ADC)-(∠PBC+∠PDC)=360°-50°-210°-75°=25°.
②当BM∥DN时,∠A=∠C.
证明:如图,连结BD.
∵BM∥DN,∴∠BDN+∠DBM=180°,∴∠FDN+∠ADB+∠ABD+∠MBE=360°-180°=180°,即(∠FDC+∠CBE)+(∠ADB+∠ABD)=180°,
∴(360°-∠ADC-∠CBA)+(180°-∠A)=180°,
∴(360°-360°+∠A+∠C)+(180°-∠A)=180°,∴∠A=∠C.
(2)如图,延长DC交BP于点Q.∵∠A=140°,∠G=100°,∠BCD=120°,∠A+∠ABC+∠BCD+∠CDG+∠G=540°,∴∠ABC+∠CDG=180°,∴∠CBE+∠CDF=360°-180°=180°,∵BP平分∠CBE,DP平分∠CDF,∴∠CBP+∠CDP=(∠CBE+∠CDF)=90°,∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,∴∠BCD=∠CBP+∠QDP+∠BPD,∴∠BPD=∠BCD-(∠CBP+∠QDP)=120°-90°=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024华东师大版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023湖南衡阳中考)下列长度的各组线段能组成一个三角形的是( )
A.1 cm,2 cm,3 cm B.3 cm,8 cm,5 cm
C.4 cm,5 cm,10 cm D.4 cm,5 cm,6 cm
2.(2023福建三明三元期中)下列各三角形中,正确画出△ABC的AC边上的高的是( )
A B C D
3.【新考法】(2023河南周口太康期末)将一副三角板按如图所示的方式摆放,其中有两边互相垂直,则∠1=( )
A.45° B.50° C.60° D.75°
4.(2023河南南阳西峡期末)下列正多边形组合不能铺满地面的是( )
A.正三角形与正方形
B.正方形与正六边形
C.正方形与正八边形
D.正三角形,正方形与正六边形
5.(2023福建南平政和模拟)具备下列条件的△ABC不是直角三角形的是( )
A.∠A=∠B=3∠C
B.∠A+∠B=∠C
C.∠A=∠B=∠C
D.∠A∶∠B∶∠C=1∶2∶3
6.(2023河南信阳淮滨期中)在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )
A.过C作EF∥AB
B.延长AC到F,过C作CE∥AB
C.作CD⊥AB于点D
D.过AB上一点D作DE∥BC,DF∥AC
7.(2023四川眉山东坡模拟)如图,已知∠MON=60°,正五边形的顶点A、B在射线OM上,顶点E在射线ON上,则∠AEO的度数为( )
A.24° B.45° C.48° D.72°
8.(2022重庆七中期中)如图,E是△ABC的BC边上的一点,且BC=3BE,点D是AC边上一点,且AD=AC,S△ABC=36,则S△BEF-S△ADF=( )
A.4.5 B.4 C.3.5 D.3
9.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260° C.270° D.360°
10.【双角平分线模型】(2023四川南充期末)如图,D为△ABC边BC延长线上一点,∠ABC与∠ACD的平分线交于点A1,∠A1BC与∠A1CD的平分线交于点A2,……,∠A2 022BC与∠A2 022CD的平分线交于点A2 023,若∠A2 023=α,则∠A=( )
A.2 022α B.2 023α C.22 022α D.22 023α
二、填空题(每小题3分,共18分)
11.(2023吉林中考)如图,钢架桥的设计中采用了三角形的结构,其数学道理是 .
12.(2023福建龙岩模拟)若三角形的三边的长都是整数,其中两边长分别为2和5,则第三边的长可以是 .(只需写出一个符合条件的整数)
13.【新独家原创】如图,五边形ABCDE中,BC∥DE,则x的值为 .
14.(2023河南鹤壁期末)如图,在△ABC中,AD是∠BAC的平分线,EG∥AD,交BC于E、AB于F、CA的延长线于G,∠B=30°,∠C=70°,则∠G的度数为 °
15.(2023四川成都四十三中期中)如图所示,在△ABC中,已知点D,E,F分别为BC,AD,BE的中点,且S△ABC=15 cm2,则图中△CEF的面积= .
16.(2023四川成都青羊树德实验中学期中)我们定义:在一个三角形中,若一个内角的度数是另一个内角度数的7倍,则这样的三角形被称为“德馨三角形”.如:三个内角分别为100°,70°,10°的三角形是“德馨三角形”.如图,点E在△ABC的边AC上,连结BE,作∠AEB的平分线交AB于点D,在BE上取点F,使∠BFD+∠BEC=180°,∠EDF=∠C.若△BCE是“德馨三角形”,则∠C的度数为 .
三、解答题(共52分)
17.(2023福建福州鼓楼延安中学期末)(6分)如图,在△ABC中,AD是BC边上的高,BE平分∠ABC.若∠ABC=70°,∠DAC=50°,求∠AEB的度数.
18.(2022广东云浮期末)(8分)若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边长均为整数,求△ABC的周长.
19.(2022湖南邵阳武冈期中)(8分)如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
20.(2023山西太原二模)(8分)如图,在凹四边形ABCD中,∠A=45°,∠B=55°,∠D=20°,求∠BCD的度数.
下面是学习小组的同学们交流时得到的解决问题的三种方法:
方法一:作射线AC;方法二:延长BC交AD于点E;方法三:连结BD.
请选择上述一种方法,求∠BCD的度数.
21.【双角平分线模型】(2023天津东丽期末)(10分)如图1,BE平分∠ABC,且与△ABC的外角∠ACD的平分线交于点E.
(1)若∠ABC=80°,∠ACB=50°,求∠E的度数;
(2)若把∠A截去,得到四边形MBCN,如图2,猜想∠E,∠M,∠N的数量关系并证明.
图1 图2
22.(2023山东日照东港泰安路中学期末)(12分)如图,多边形的外角∠CBE和∠CDF的平分线分别为BM,DN.
(1)若多边形为四边形ABCD.
①如图1,∠A=50°,∠C=100°,BM与DN交于点P,求∠BPD的度数;
②如图2,猜测当BM∥DN时,∠A和∠C满足什么数量关系,并证明你的猜想.
(2)如图3,若多边形是五边形ABCDG,已知∠A=140°,∠G=100°,∠BCD=120°,BM与DN交于点P,求∠BPD的度数.
图1 图2
图3
答案全解全析
1.D A.∵1+2=3,∴长度为1 cm,2 cm,3 cm的三条线段不能组成三角形,本选项不符合题意;B.∵3+5=8,∴长度为3 cm,8 cm,5 cm的三条线段不能组成三角形,本选项不符合题意;C.∵4+5<10,∴长度为4 cm,5 cm,10 cm的三条线段不能组成三角形,本选项不符合题意;D.∵4+5>6,∴长度为4 cm,5 cm,6 cm的三条线段能组成三角形,本选项符合题意.故选D.
2.D 过点B作AC所在直线的垂线段,该垂线段即为△ABC的AC边上的高,∴四个选项中只有选项D符合题意.故选D.
3.D 本题以一副三角板组合图为背景,考查对三角形外角的性质的理解与把握.如图,由题意可知,∠2=45°,∠4=30°,
∴∠3=90°-∠2=45°,∴∠1=∠3+∠4=45°+30°=75°,故选D.
4.B A.正三角形的每个内角是60°,正方形的每个内角是90°,∵3×60°+2×90°=360°,∴能铺满地面;B.正方形的每个内角是90°,正六边形的每个内角是120°,令90m+120n=360,得m=4-n,显然n取任何正整数时,m都不能得正整数,故不能铺满;C.正方形的每个内角是90°,正八边形的每个内角是135°,∵90°+2×135°=360°,∴能铺满地面;D.正三角形的每个内角是60°,正方形的每个内角是90°,正六边形的每个内角是120°,∵60°+2×90°+120°=360°,∴能铺满地面.故选B.
5.A A.由∠A=∠B=3∠C及∠A+∠B+∠C=180°可得∠A=∠B=,∠C=,△ABC不是直角三角形,故符合题意;B.由∠A+∠B=∠C及∠A+∠B+∠C=180°可得∠C=90°,△ABC是直角三角形,故不符合题意;C.由∠A=∠B=∠C及∠A+∠B+∠C=180°可得∠C=90°,∠A=∠B=45°,△ABC是直角三角形,故不符合题意;D.由∠A∶∠B∶∠C=1∶2∶3及∠A+∠B+∠C=180°可得∠C=90°,∠A=30°,∠B=60°,△ABC是直角三角形,故不符合题意.故选A.
6.C A.由EF∥AB,得∠ECA=∠A,∠FCB=∠B.由∠ECA+∠ACB+∠FCB=180°,得∠A+∠ACB+∠B=180°,故A不符合题意.B.由CE∥AB,得∠A=∠FCE,∠B=∠BCE.由∠FCE+∠ECB+∠ACB=180°,得∠A+∠B+∠ACB=180°,故B不符合题意.C.由CD⊥AB于D,得∠ADC=∠CDB=90°,无法证得三角形内角和是180°,故C符合题意.D.由DF∥AC,得∠EDF=∠AED,∠A=∠FDB.由ED∥CB,得∠EDA=∠B,∠C=∠AED,那么∠C=∠EDF.由∠ADE+∠EDF+∠FDB=180°,得∠B+∠C+∠A=180°,故D不符合题意.故选C.
7.C ∵五边形ABCDE为正五边形,∴∠BAE=(5-2)×180°÷5=108°,∵∠MON=60°,∴∠AEO=∠BAE-
∠MON=108°-60°=48°,故选C.
8.D ∵BC=3BE,AD=AC,S△ABC=36,∴S△ABE=S△ABC=×36=12,S△ABD=S△ABC=9,∴S△BEF-S△ADF=S△ABE-S△ABD=12-9=3,故选D.
9.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+∠D+∠E+∠C=180°,故选A.
10.D 在△ABC中,∠A=∠ACD-∠ABC,∵∠ABC的平分线与∠ACD的平分线交于点A1,∴∠A1=∠A1CD-∠A1BC=(∠ACD-∠ABC)=∠A,同理可得∠A2=∠A1=∠A,∠A3=∠A2=∠A,……,
∠An=∠A,∵∠A2 023=α,∴∠A=α,即∠A=22 023α.故选D.
11.三角形具有稳定性
12.4(答案不唯一)
解析 设第三边长为x,∵三角形的两边长分别为2和5,∴5-2
解析 ∵BC∥DE,∴∠C+∠D=180°,∵∠A+∠B+∠C+∠D+∠E=(5-2)×180°=540°,∴x+x+10+x-40+180=540,解得x=130.故答案为130.
14.40
解析 ∵∠B=30°,∠C=70°,∴∠BAC=180°-∠B-∠C=80°.∵AD平分∠BAC,∴∠DAC=∠BAC=40°.∵EG∥AD,∴∠G=
∠DAC=40°.故答案为40.
15. cm2
解析 ∵点D,E,F分别为BC,AD,BE的中点,∴S△ABD=2S△BDE,S△ADC=2S△CDE,S△EBC=2S△CEF,∵S△ABC=S△ABD+S△ADC,S△ECB=S△BDE+S△CDE,∴S△ABC=2S△BCE,∴S△ABC=4S△CEF,∵S△ABC=15 cm2,∴S△CEF=×15=(cm2),故答案为 cm2.
16.20°或84°
解析 ∵∠BFD+∠BEC=180°,∠BEC+∠AEB=180°,∴∠BFD=∠AEB,∴AC∥DF,∴∠AED=∠EDF,∵∠EDF=∠C,∴∠C=∠AED,∴DE∥BC,∴∠BED=∠CBE,∵ED平分∠AEB,∴∠AED=∠BED,∴∠C=∠CBE.∵△BCE是“德馨三角形”,∴当7∠C=∠BEC时,∠C+∠C+7∠C=180°,解得∠C=20°;当7∠BEC=∠C时,∠C+∠C+∠C=180°,解得∠C=84°.故答案为20°或84°.
17.解析 ∵AD是BC边上的高,∴∠ADC=90°,在Rt△ACD中,∠C=90°-∠DAC=90°-50°=40°,∵BE平分∠ABC,∴∠EBC=∠ABC=×70°=35°,∴∠AEB=∠EBC+∠C=35°+40°=75°.
18.解析 (1)根据三角形的三边关系,得
解得3
20.解析 方法一:作射线AC,如图,由三角形外角的性质,得∠1=∠B+∠3,∠2=∠4+∠D,
所以∠1+∠2=∠B+∠3+∠4+∠D=∠B+∠D+∠BAD=55°+20°+45°=120°.
方法二:延长BC交AD于点E,如图,
∵∠CED=∠A+∠B,∠BCD=∠CED+∠D,
∴∠BCD=∠A+∠B+∠D=45°+55°+20°=120°.
方法三:连结BD,如图.
由三角形内角和定理,得∠A+∠ABD+∠ADB=180°,因为∠A=45°,∠ABC=55°,∠ADC=20°,所以∠CBD+∠CDB=180°-(45°+55°+20°)=60°,在△BDC中,由三角形内角和定理,得∠BCD=180°-60°=120°.
21.解析 (1)∵BE平分∠ABC,CE平分∠ACD,
∴∠EBC=∠ABC,∠ECD=∠ACD,
∵∠ACD=∠A+∠ABC,∠ECD=∠E+∠EBC,
∴∠ACD=∠E+∠EBC,
∴(∠A+∠ABC)=∠E+∠EBC,∴∠A+∠ABC=∠E+∠EBC,∴∠A=∠E,
∵∠A=180°-∠ABC-∠ACB,∠ABC=80°,∠ACB=50°,∴∠A=50°,∴∠E=25°.
(2)∠E=(∠BMN+∠MNC-180°).证明:分别延长BM和CN相交于点A,如图,∵∠A+∠AMN+∠ANM=180°,∠AMN+∠BMN=180°,∠ANM+∠MNC=180°,∴∠A=180°-(∠AMN+∠ANM)=180°-(180°-∠BMN+180°-∠MNC)=∠BMN+∠MNC-180°,
又由(1)知∠E=∠A,∴∠E=(∠BMN+∠MNC-180°).
22.解析 (1)①∵∠A=50°,∠C=100°,∴在四边形ABCD中,∠ABC+∠ADC=360°-∠A-∠C=210°,∴∠CBE+∠CDF=150°.∵∠CBE和∠CDF的平分线分别为BM,DN,∴∠PBC+∠PDC=∠CBE+∠CDF=(∠CBE+∠CDF)=×150°=75°,
∴∠BPD=360°-∠A-(∠ABC+∠ADC)-(∠PBC+∠PDC)=360°-50°-210°-75°=25°.
②当BM∥DN时,∠A=∠C.
证明:如图,连结BD.
∵BM∥DN,∴∠BDN+∠DBM=180°,∴∠FDN+∠ADB+∠ABD+∠MBE=360°-180°=180°,即(∠FDC+∠CBE)+(∠ADB+∠ABD)=180°,
∴(360°-∠ADC-∠CBA)+(180°-∠A)=180°,
∴(360°-360°+∠A+∠C)+(180°-∠A)=180°,∴∠A=∠C.
(2)如图,延长DC交BP于点Q.∵∠A=140°,∠G=100°,∠BCD=120°,∠A+∠ABC+∠BCD+∠CDG+∠G=540°,∴∠ABC+∠CDG=180°,∴∠CBE+∠CDF=360°-180°=180°,∵BP平分∠CBE,DP平分∠CDF,∴∠CBP+∠CDP=(∠CBE+∠CDF)=90°,∵∠BCD=∠CBP+∠CQB,∠CQB=∠QDP+∠BPD,∴∠BCD=∠CBP+∠QDP+∠BPD,∴∠BPD=∠BCD-(∠CBP+∠QDP)=120°-90°=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
