三角形的三边关系

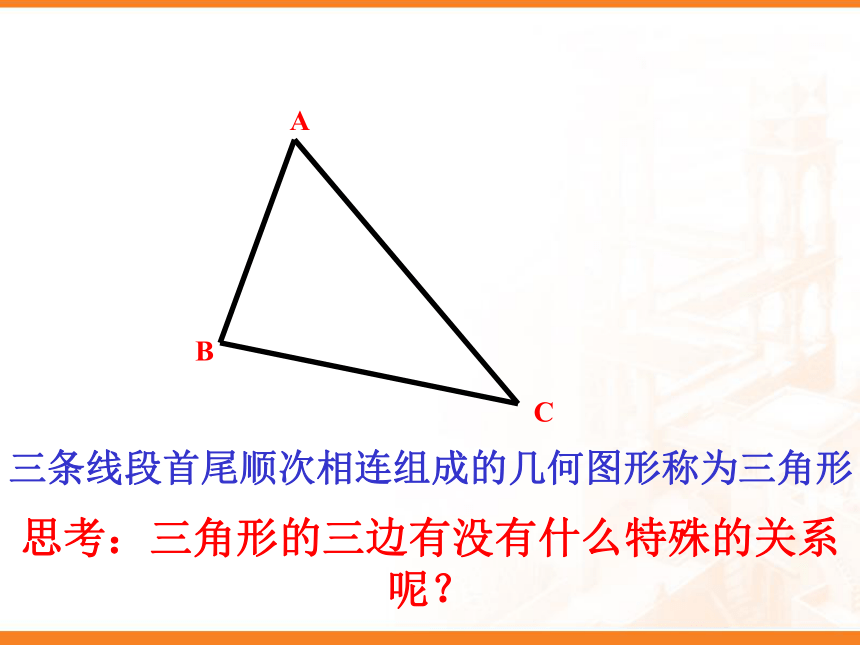
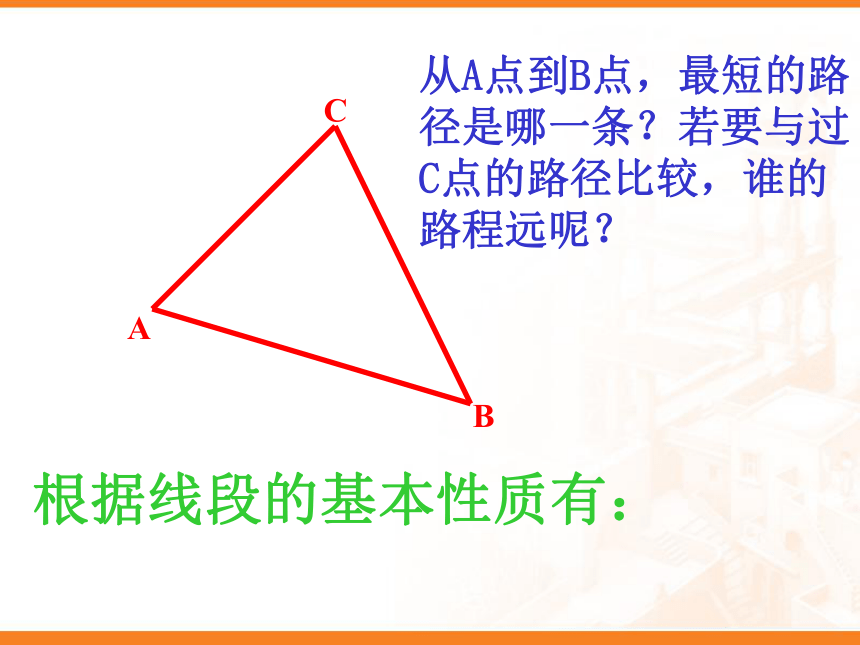
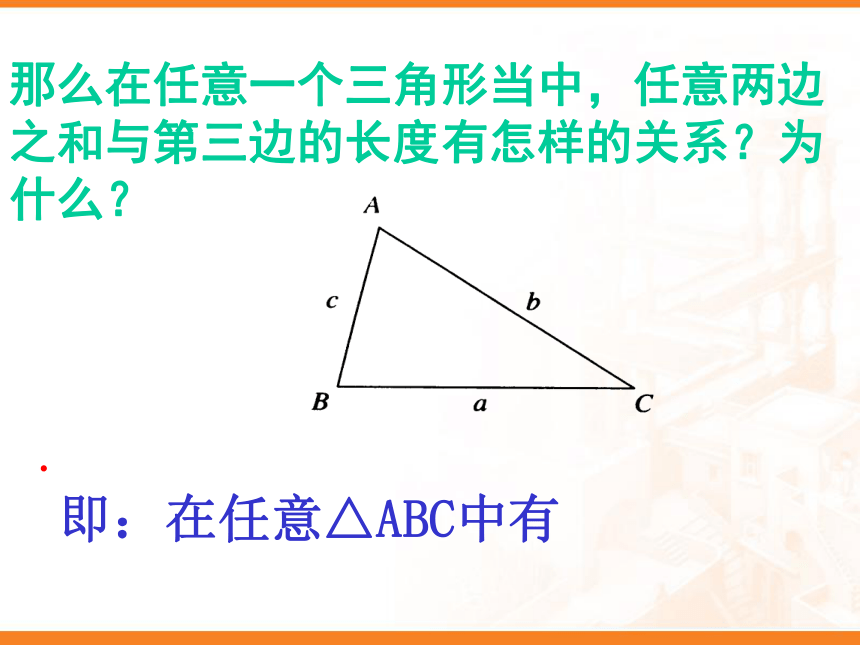
课件18张PPT。欢迎领导和老师们的指导 黔江区冯家中学: 谢代兵 授课班级：七年级BAC 三条线段首尾顺次相连组成的几何图形称为三角形 思考：三角形的三边有没有什么特殊的关系呢？三角形的三边关系 有两根长度分别为4cm和6cm的木棒，用长度为10cm的木棒与它们能摆成三角形吗？为什么？A BC 从A点到B点，最短的路径是哪一条？若要与过C点的路径比较，谁的路程远呢？ 根据线段的基本性质有：那么在任意一个三角形当中，任意两边之和与第三边的长度有怎样的关系？为什么？.即：在任意△ABC中有
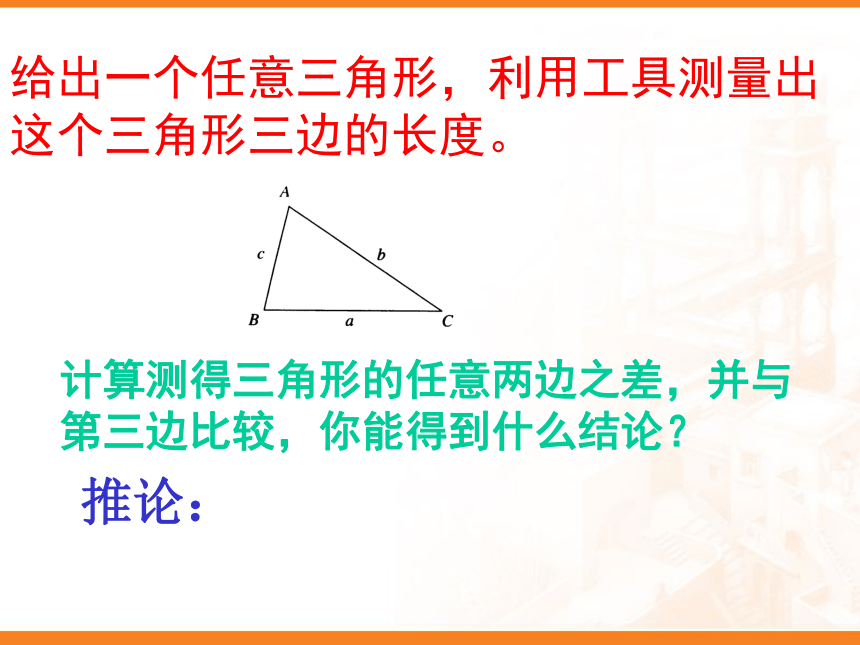
给出一个任意三角形，利用工具测量出这个三角形三边的长度。计算测得三角形的任意两边之差，并与第三边比较，你能得到什么结论？推论：1、判断三条已知线段能否组成三角形：小结：
　若两条较短边的和大于最长边，
则可构成三角形，否则不能. 两边之差＜第三边＜两边之和 2、确定三角形第三边的取值范围：练一练一个三角形两边分别为75㎝、85㎝请问它的第三边应在哪个范围内呢？
有两根长度分别为5㎝、8㎝的木棒，现在再取一根木棒与它们拼成一个 三角形。用3㎝的木棒行吗？14㎝的木棒呢？你认为要多长的木棒才行呢？例1：在△ABC中，AC=5，BC=2，并且AB是奇数。求△ABC的周长。（1）这些建筑物当中都有那些相似之处 ？【思考】请同学们观察下面两幅图片：再观察下面的图形：（2）为什么都用这种几何图形 ？三角形的稳定性：如果三角形的三边固定，那么三角形的形状和大小就完全确定了【原理】例2：
若一个等腰三角形的周长为18cm。
（1）腰比底边的2倍多3cm，求各边的长。
（2）已知其中一边的长为4cm，求各边的长。
（3）若底边长是偶数，求三边的长。
例3：如图，O为 内一点.
求证：谢谢同学们和我的合作