2015年中考数学易错题赏析:(六)三角形(2)
文档属性
| 名称 | 2015年中考数学易错题赏析:(六)三角形(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-12 00:00:00 | ||
图片预览




文档简介
(六)三角形(2)
易错题赏析
易错点8:直角三角形的性质与判定,特别注意的两条性质:直角三角形中30°角所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半.
易错题9:如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,则CH的长为……………………………………………………………( )
A.2.5 B. C. D.2
错解:D
正解:B
赏析:本题由于不能准确找到直角三角形并利用“直角三角形中斜边上的中线等于斜边的一半”的性质而造成错解.21·cn·jy·com
正确的解法是:如图,连接AC、CF,∵在正方形ABCD和正方形CEFG中,BC=1,CE=3,∴由勾股定理或三角函数可得AC=,CF=3,又∵∠ACD=∠FCG=45°,∴∠ACF=90°,在Rt△ACF中,由勾股定理,得AF===2,又∵H是AF的中点,∴CH=AF=×2=.不善于添加辅助线来求解问题也是造成错解的主要原因之一.2·1·c·n·j·y
易错点9:勾股定理及其逆定理的综合应用,在运用勾股定理及其逆定理计算或证明有关问题时面积法的运用.
易错题10:如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_______________.【来源:21·世纪·教育·网】
错解:3
正解:3或
赏析:本题只考虑了∠B′EC=90°的一种情况而造成错解.
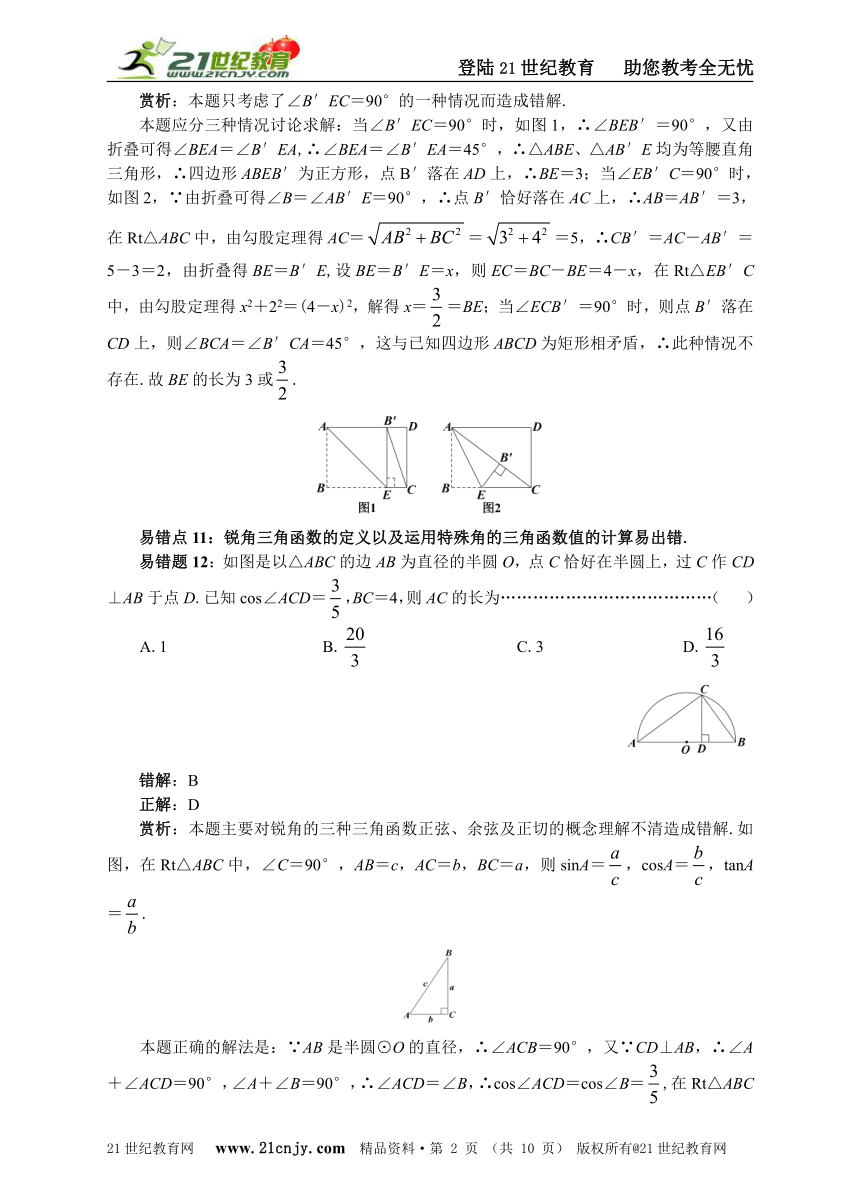
本题应分三种情况讨论求解:当∠B′EC=90°时,如图1,∴∠BEB′=90°,又由折叠可得∠BEA=∠B′EA,∴∠BEA=∠B′EA=45°,∴△ABE、△AB′E均为等腰直角三角形,∴四边形ABEB′为正方形,点B′落在AD上,∴BE=3;当∠EB′C=90°时,如图2,∵由折叠可得∠B=∠AB′E=90°,∴点B′恰好落在AC上,∴AB=AB′=3,在Rt△ABC中,由勾股定理得AC===5,∴CB′=AC-AB′=5-3=2,由折叠得BE=B′E,设BE=B′E=x,则EC=BC-BE=4-x,在Rt△EB′C中,由勾股定理得x2+22=(4-x)2,解得x==BE;当∠ECB′=90°时,则点B′落在CD上,则∠BCA=∠B′CA=45°,这与已知四边形ABCD为矩形相矛盾,∴此种情况不存在.故BE的长为3或.21·世纪*教育网
易错点11:锐角三角函数的定义以及运用特殊角的三角函数值的计算易出错.
易错题12:如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于点D.已知cos∠ACD=,BC=4,则AC的长为…………………………………( )
A.1 B. C.3 D.
错解:B
正解:D
赏析:本题主要对锐角的三种三角函数正弦、余弦及正切的概念理解不清造成错解.如图,在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,则sinA=,cosA=,tanA=.www-2-1-cnjy-com
本题正确的解法是:∵AB是半圆⊙O的直径,∴∠ACB=90°,又∵CD⊥AB,∴∠A+∠ACD=90°,∠A+∠B=90°,∴∠ACD=∠B,∴cos∠ACD=cos∠B=,在Rt△ABC中,cos∠B=,∴=,解得AB=,在Rt△ABC中,由勾股定理得AC===.(也可用∠B的正弦或正切求解)
易错点12:解直角三角形的应用,特别要注意通过作辅助线将图形转化为直角三角形的方法.
易错题13:为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出_______个这样的停车位.(=1.4)2-1-c-n-j-y
错解:18
正解:17
赏析:本题可能对题意没有理解清楚,不知怎样求每个车位所占路段长而导致错解,也可能是计算出错导致错解. 21*cnjy*com
正确的解法是:首先计算右侧第一个车位所占路段长:如图1,由题意,得△ACB、△EDB均为等腰直角三角形,在△EDB中,cos∠EBD=,∴BD=BE cos∠EBD=2.2×=1.1×1.4=1.54,同理,CB=AB cos∠ABC=5×=2.5×1.4=3.5,∴CD=CB+BD=1.54+3.5=5.04(米),即第一个车位所占路段长;再计算每增加一个车位所需路段长:如图2,由题意,得△ABC为等腰直角三角形,∵cos∠CAB=,∴AB==2.2×=2.2×1.4=3.08(米),即每增加一个车位所需路段长;接下来,可设可以划出x个车位,由题意,得5.04+3.08(x-1)≤56,解得x≤≈17.5,∵x取最大整数,∴x=17.注意:本题结果取近似值时应采用去尾法,只舍不入,这也是造成本题错解的可能原因之一.【来源:21cnj*y.co*m】
易错点13:相似三角形的性质,三角形相似的判定.
易错题14:如图,在直角三角形ABC中,∠C=90°,其内部放置边长分别为3,4,x的三个正方形,则x的值为…………………………………………………………………( )
A.5 B.6 C.7 D.8
错解:A
正解:C
赏析:本题图形中,相似三角形比较多,由于不能准确找出哪两个相似三角形来求解,从而造成错解.
本题应找出能够用3,4,x或含x的式子表示出三边的两个相似三角形,然后利用相似三角形的性质来求解,如图,∵∠C=90°,∴∠CFG+∠CGF=90°,又∵∠EFG=90°,∴∠DFE+∠CFG=90°,∴∠DFE=∠CGF,又∵FG∥HM,∴∠CGF=∠GMH,∴∠DFE=∠GMH,又∵∠DEG=∠GHM=90°,∴△DFE∽△GMH,∴,∵DE=3,GH=x-4,FE=x-3,MH=4,∴,化简得x2-7x=0,∴x1=0,x2=7,∵x>0,∴x=7.21世纪教育网版权所有
易错点14:相似三角形面积之比等于相似比的平方.
易错题15:如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=_______.
错解:
正解:
赏析:本题可能以为相似三角形的面积之比等于相似比而造成错解,相似三角形的面积之比等于相似比的平方.
正确的解法应是:∵S△ADE=S四边形DBCE,∴设S△ADE=x,则S四边形DBCE=x,∴S△ABC=x+x=2x,∴,又∵DE∥BC,∴△ADE∽△ABC,∴,∴,∴.【出处:21教育名师】
易错点15:相似与全等的综合运用;相似与锐角三角函数的综合运用.
易错题16:如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于点G.【版权所有:21教育】
(1)若M为边AD的中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
错解:(1)证明:如图1,∵四边形ABCD是矩形,∴∠A=∠MDF=90°,∵M为边AD的中点,∴MA=MD,在△MAE和△MDF中,∵,∴△MAE≌△MDF(AAS),∴EM=FM,又∵MG⊥EM,∴EG=FG,∴△EFG是等腰三角形;
(2)解:如图2,∵AB=3,AD=4,AE=1,AM=a,∴BE=AB-AE=3-1=2,BC=AD=4,在Rt△EAM中,∵EM2=AE2+AM2,∴EM2=1+a2,在Rt△EBC中,∵EC2=BE2+BC2,∴EC2=22+42=4+16=20. 在Rt△EMC中,∵EM2=EC2+EM2,∴CM2=20+(1+a2)=20+1+a2=21+a2,∴CM=.∵点G与点C重合,∴GM=.
(3)如图3,∵AB=3,AD=4,AE=1,AM=a,∴MD=AD-AM=4-a,在Rt△EAM中,∵EM2=AE2+AM2,∴EM=.∵∠A=∠MDF=90°,∠AME=∠DMF,∴△MAE∽△MDF,∴,∴,∴FM=,∴EF=EM+FM=+=.由(2)得,MG=,∴△EFG的面积S=×EF×MG=××=,∴当a=2时,S最小,为S==. 21教育名师原创作品
正解:(1)证明:如图1,∵四边形ABCD是矩形,
∴∠A=∠MDF=90°,
∵M为边AD的中点,
∴MA=MD,
在△MAE和△MDF中,∵,
∴△MAE≌△MDF(ASA),
∴EM=FM,
又∵MG⊥EM,
∴EG=FG,
∴△EFG是等腰三角形;
(2)解:如图2,∵AB=3,AD=4,AE=1,AM=a,
∴BE=AB-AE=3-1=2,BC=AD=4,
在Rt△EAM中,∵EM2=AE2+AM2,
∴EM2=1+a2,
在Rt△EBC中,∵EC2=BE2+BC2,
∴EC2=22+42=4+16=20.
在Rt△EMC中,∵EM2=EC2-EM2,
∴CM2=20-(1+a2)=20-1-a2=19-a2,
∴CM=.
∵点G与点C重合,
∴GM=.
(3)如图4,过点M作MN⊥BC于点N,
∵AB=3,AD=4,AE=1,AM=a,
∴MD=AD-AM=4-a,
在Rt△EAM中,∵EM2=AE2+AM2,
∴EM=.
∵∠A=∠MDF=90°,∠AME=∠DMF,
∴△MAE∽△MDF,
∴,
∴,
∴FM=,
∴EF=EM+FM=+=.
∵AD∥BC,
∴∠MGN=∠DMG,
∵∠AME+∠AEM=90°,∠AME+∠DMG=90°,
∴∠AEM=∠DMG,
∴∠MGN=∠AEM,
∵∠MNG=∠MAE=90°,
∴△MNG∽△MAE,
∴,
∴,
∴MG=,
∴△EFG的面积S=×EF×MG=××=,
∵a2越大,S就越小,且S为最小整数值,
∴当a2=6,即a=时,S有最小整数值,为S=1+6=7.
赏析:第一小题错在对全等的两种判定方法ASA和AAS没有分清楚,第二小题错在第三次运用勾股定理时出现了错误,第三小题错在把第二小题的结论拿到这里来用,因为条件变了,不能拿来用,应另求高MG的值.本题综合了全等三角形,等腰三角形,直角三角形和相似三角形的有关内容,且涉及函数的最值问题,是一道非常好的三角形综合题,需要同学们具有较高的分析问题、解决问题的能力.www.21-cn-jy.com
易错练
1. 如图,四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB,若DG=3,EC=1,则DE的长为……………………( )
A.2 B.2 C. D.
2.如图是拦水坝的横断面,斜坡AB的水平宽度为15米,斜面坡度为1︰3,则斜坡AB的长为…………………………………………………………………………………………( )
A.5米 B.5米 C.10米 D.30米
3.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=1,则S四边形ABFE=________________.21cnjy.com
4.小明坐于堤边垂钓,河堤AC的坡角为30°,AC长米.钓竿AO的倾斜角是60°,其长度为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
5.在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.21教育网
(1)如图1,AC︰AB=1︰2,EF⊥CB于点F.求证:EF=CD.
(2)如图2,AC︰AB=1︰,EF⊥CE于点E.求EF︰EG的值.
参考答案
2.C 解析:过点B作BE⊥AD于点E,
由题意得AE=15,,解得BE=5,
∴在Rt△AEB中,由勾股定理得AB=(米).
∵S△DEF=1,
∴S△CBF=4,
又∵,
∴S△CDF=2,
∴S△BCD=S△CBF+S△CDF=2+4=6,
∴S△ADB=S△BCD=6,
∴S四边形ABFE=S△ADB-S△DEF=6-1=5.
4.解:延长OA交BC于点D,
∵AO的倾斜角是60°,
∴∠ODB=60°,
∵∠ACD=30°,
∴∠CAD=180°-∠ODB-∠ACD=90°.
5.解:(1)证明:∵AC︰AB=1︰2,点E为AB的中点,
∴AC=BE.
∵∠CAB=90°,AD⊥BC,
∴∠B=∠DAC.
∵AD⊥BC,EF⊥CB,
∴∠ADC=∠EFB=90°,
∴△EFB≌△CDA,
∴EF=CD.
(2)解:如图3,过点E作EM⊥BD于点M,EN⊥AD于点N.
∵AD⊥BC,
∴四边形DNEM为矩形,∴∠NEM=90°.
又EF⊥CE,∴∠NEG=∠MEF,∵∠ENG=∠EMF=90°,
∴△EMF∽△ENG,∴.
∵AD⊥BC,∴tan∠B=,∵AC︰AB=1︰,
∴tan∠B=1︰=,∴∠B=30°,∴∠NAE=60°,
∴sin∠NAE=,∴EN=AE,
易错题赏析
易错点8:直角三角形的性质与判定,特别注意的两条性质:直角三角形中30°角所对的直角边等于斜边的一半;直角三角形斜边上的中线等于斜边的一半.
易错题9:如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,则CH的长为……………………………………………………………( )
A.2.5 B. C. D.2
错解:D
正解:B
赏析:本题由于不能准确找到直角三角形并利用“直角三角形中斜边上的中线等于斜边的一半”的性质而造成错解.21·cn·jy·com
正确的解法是:如图,连接AC、CF,∵在正方形ABCD和正方形CEFG中,BC=1,CE=3,∴由勾股定理或三角函数可得AC=,CF=3,又∵∠ACD=∠FCG=45°,∴∠ACF=90°,在Rt△ACF中,由勾股定理,得AF===2,又∵H是AF的中点,∴CH=AF=×2=.不善于添加辅助线来求解问题也是造成错解的主要原因之一.2·1·c·n·j·y
易错点9:勾股定理及其逆定理的综合应用,在运用勾股定理及其逆定理计算或证明有关问题时面积法的运用.
易错题10:如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_______________.【来源:21·世纪·教育·网】
错解:3
正解:3或
赏析:本题只考虑了∠B′EC=90°的一种情况而造成错解.
本题应分三种情况讨论求解:当∠B′EC=90°时,如图1,∴∠BEB′=90°,又由折叠可得∠BEA=∠B′EA,∴∠BEA=∠B′EA=45°,∴△ABE、△AB′E均为等腰直角三角形,∴四边形ABEB′为正方形,点B′落在AD上,∴BE=3;当∠EB′C=90°时,如图2,∵由折叠可得∠B=∠AB′E=90°,∴点B′恰好落在AC上,∴AB=AB′=3,在Rt△ABC中,由勾股定理得AC===5,∴CB′=AC-AB′=5-3=2,由折叠得BE=B′E,设BE=B′E=x,则EC=BC-BE=4-x,在Rt△EB′C中,由勾股定理得x2+22=(4-x)2,解得x==BE;当∠ECB′=90°时,则点B′落在CD上,则∠BCA=∠B′CA=45°,这与已知四边形ABCD为矩形相矛盾,∴此种情况不存在.故BE的长为3或.21·世纪*教育网
易错点11:锐角三角函数的定义以及运用特殊角的三角函数值的计算易出错.
易错题12:如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CD⊥AB于点D.已知cos∠ACD=,BC=4,则AC的长为…………………………………( )
A.1 B. C.3 D.
错解:B
正解:D
赏析:本题主要对锐角的三种三角函数正弦、余弦及正切的概念理解不清造成错解.如图,在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,则sinA=,cosA=,tanA=.www-2-1-cnjy-com
本题正确的解法是:∵AB是半圆⊙O的直径,∴∠ACB=90°,又∵CD⊥AB,∴∠A+∠ACD=90°,∠A+∠B=90°,∴∠ACD=∠B,∴cos∠ACD=cos∠B=,在Rt△ABC中,cos∠B=,∴=,解得AB=,在Rt△ABC中,由勾股定理得AC===.(也可用∠B的正弦或正切求解)
易错点12:解直角三角形的应用,特别要注意通过作辅助线将图形转化为直角三角形的方法.
易错题13:为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米,宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出_______个这样的停车位.(=1.4)2-1-c-n-j-y
错解:18
正解:17
赏析:本题可能对题意没有理解清楚,不知怎样求每个车位所占路段长而导致错解,也可能是计算出错导致错解. 21*cnjy*com
正确的解法是:首先计算右侧第一个车位所占路段长:如图1,由题意,得△ACB、△EDB均为等腰直角三角形,在△EDB中,cos∠EBD=,∴BD=BE cos∠EBD=2.2×=1.1×1.4=1.54,同理,CB=AB cos∠ABC=5×=2.5×1.4=3.5,∴CD=CB+BD=1.54+3.5=5.04(米),即第一个车位所占路段长;再计算每增加一个车位所需路段长:如图2,由题意,得△ABC为等腰直角三角形,∵cos∠CAB=,∴AB==2.2×=2.2×1.4=3.08(米),即每增加一个车位所需路段长;接下来,可设可以划出x个车位,由题意,得5.04+3.08(x-1)≤56,解得x≤≈17.5,∵x取最大整数,∴x=17.注意:本题结果取近似值时应采用去尾法,只舍不入,这也是造成本题错解的可能原因之一.【来源:21cnj*y.co*m】
易错点13:相似三角形的性质,三角形相似的判定.
易错题14:如图,在直角三角形ABC中,∠C=90°,其内部放置边长分别为3,4,x的三个正方形,则x的值为…………………………………………………………………( )
A.5 B.6 C.7 D.8
错解:A
正解:C
赏析:本题图形中,相似三角形比较多,由于不能准确找出哪两个相似三角形来求解,从而造成错解.
本题应找出能够用3,4,x或含x的式子表示出三边的两个相似三角形,然后利用相似三角形的性质来求解,如图,∵∠C=90°,∴∠CFG+∠CGF=90°,又∵∠EFG=90°,∴∠DFE+∠CFG=90°,∴∠DFE=∠CGF,又∵FG∥HM,∴∠CGF=∠GMH,∴∠DFE=∠GMH,又∵∠DEG=∠GHM=90°,∴△DFE∽△GMH,∴,∵DE=3,GH=x-4,FE=x-3,MH=4,∴,化简得x2-7x=0,∴x1=0,x2=7,∵x>0,∴x=7.21世纪教育网版权所有
易错点14:相似三角形面积之比等于相似比的平方.
易错题15:如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=_______.
错解:
正解:
赏析:本题可能以为相似三角形的面积之比等于相似比而造成错解,相似三角形的面积之比等于相似比的平方.
正确的解法应是:∵S△ADE=S四边形DBCE,∴设S△ADE=x,则S四边形DBCE=x,∴S△ABC=x+x=2x,∴,又∵DE∥BC,∴△ADE∽△ABC,∴,∴,∴.【出处:21教育名师】
易错点15:相似与全等的综合运用;相似与锐角三角函数的综合运用.
易错题16:如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于点G.【版权所有:21教育】
(1)若M为边AD的中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
错解:(1)证明:如图1,∵四边形ABCD是矩形,∴∠A=∠MDF=90°,∵M为边AD的中点,∴MA=MD,在△MAE和△MDF中,∵,∴△MAE≌△MDF(AAS),∴EM=FM,又∵MG⊥EM,∴EG=FG,∴△EFG是等腰三角形;
(2)解:如图2,∵AB=3,AD=4,AE=1,AM=a,∴BE=AB-AE=3-1=2,BC=AD=4,在Rt△EAM中,∵EM2=AE2+AM2,∴EM2=1+a2,在Rt△EBC中,∵EC2=BE2+BC2,∴EC2=22+42=4+16=20. 在Rt△EMC中,∵EM2=EC2+EM2,∴CM2=20+(1+a2)=20+1+a2=21+a2,∴CM=.∵点G与点C重合,∴GM=.
(3)如图3,∵AB=3,AD=4,AE=1,AM=a,∴MD=AD-AM=4-a,在Rt△EAM中,∵EM2=AE2+AM2,∴EM=.∵∠A=∠MDF=90°,∠AME=∠DMF,∴△MAE∽△MDF,∴,∴,∴FM=,∴EF=EM+FM=+=.由(2)得,MG=,∴△EFG的面积S=×EF×MG=××=,∴当a=2时,S最小,为S==. 21教育名师原创作品
正解:(1)证明:如图1,∵四边形ABCD是矩形,
∴∠A=∠MDF=90°,
∵M为边AD的中点,
∴MA=MD,
在△MAE和△MDF中,∵,
∴△MAE≌△MDF(ASA),
∴EM=FM,
又∵MG⊥EM,
∴EG=FG,
∴△EFG是等腰三角形;
(2)解:如图2,∵AB=3,AD=4,AE=1,AM=a,
∴BE=AB-AE=3-1=2,BC=AD=4,
在Rt△EAM中,∵EM2=AE2+AM2,
∴EM2=1+a2,
在Rt△EBC中,∵EC2=BE2+BC2,
∴EC2=22+42=4+16=20.
在Rt△EMC中,∵EM2=EC2-EM2,
∴CM2=20-(1+a2)=20-1-a2=19-a2,
∴CM=.
∵点G与点C重合,
∴GM=.
(3)如图4,过点M作MN⊥BC于点N,
∵AB=3,AD=4,AE=1,AM=a,
∴MD=AD-AM=4-a,
在Rt△EAM中,∵EM2=AE2+AM2,
∴EM=.
∵∠A=∠MDF=90°,∠AME=∠DMF,
∴△MAE∽△MDF,
∴,
∴,
∴FM=,
∴EF=EM+FM=+=.
∵AD∥BC,
∴∠MGN=∠DMG,
∵∠AME+∠AEM=90°,∠AME+∠DMG=90°,
∴∠AEM=∠DMG,
∴∠MGN=∠AEM,
∵∠MNG=∠MAE=90°,
∴△MNG∽△MAE,
∴,
∴,
∴MG=,
∴△EFG的面积S=×EF×MG=××=,
∵a2越大,S就越小,且S为最小整数值,
∴当a2=6,即a=时,S有最小整数值,为S=1+6=7.
赏析:第一小题错在对全等的两种判定方法ASA和AAS没有分清楚,第二小题错在第三次运用勾股定理时出现了错误,第三小题错在把第二小题的结论拿到这里来用,因为条件变了,不能拿来用,应另求高MG的值.本题综合了全等三角形,等腰三角形,直角三角形和相似三角形的有关内容,且涉及函数的最值问题,是一道非常好的三角形综合题,需要同学们具有较高的分析问题、解决问题的能力.www.21-cn-jy.com
易错练
1. 如图,四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB,若DG=3,EC=1,则DE的长为……………………( )
A.2 B.2 C. D.
2.如图是拦水坝的横断面,斜坡AB的水平宽度为15米,斜面坡度为1︰3,则斜坡AB的长为…………………………………………………………………………………………( )
A.5米 B.5米 C.10米 D.30米
3.如图,在□ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEF=1,则S四边形ABFE=________________.21cnjy.com
4.小明坐于堤边垂钓,河堤AC的坡角为30°,AC长米.钓竿AO的倾斜角是60°,其长度为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
5.在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.21教育网
(1)如图1,AC︰AB=1︰2,EF⊥CB于点F.求证:EF=CD.
(2)如图2,AC︰AB=1︰,EF⊥CE于点E.求EF︰EG的值.
参考答案
2.C 解析:过点B作BE⊥AD于点E,
由题意得AE=15,,解得BE=5,
∴在Rt△AEB中,由勾股定理得AB=(米).
∵S△DEF=1,
∴S△CBF=4,
又∵,
∴S△CDF=2,
∴S△BCD=S△CBF+S△CDF=2+4=6,
∴S△ADB=S△BCD=6,
∴S四边形ABFE=S△ADB-S△DEF=6-1=5.
4.解:延长OA交BC于点D,
∵AO的倾斜角是60°,
∴∠ODB=60°,
∵∠ACD=30°,
∴∠CAD=180°-∠ODB-∠ACD=90°.
5.解:(1)证明:∵AC︰AB=1︰2,点E为AB的中点,
∴AC=BE.
∵∠CAB=90°,AD⊥BC,
∴∠B=∠DAC.
∵AD⊥BC,EF⊥CB,
∴∠ADC=∠EFB=90°,
∴△EFB≌△CDA,
∴EF=CD.
(2)解:如图3,过点E作EM⊥BD于点M,EN⊥AD于点N.
∵AD⊥BC,
∴四边形DNEM为矩形,∴∠NEM=90°.
又EF⊥CE,∴∠NEG=∠MEF,∵∠ENG=∠EMF=90°,
∴△EMF∽△ENG,∴.
∵AD⊥BC,∴tan∠B=,∵AC︰AB=1︰,
∴tan∠B=1︰=,∴∠B=30°,∴∠NAE=60°,
∴sin∠NAE=,∴EN=AE,
同课章节目录
