第23章旋转 解答题题型分类专题训练(含答案) 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第23章旋转 解答题题型分类专题训练(含答案) 2023-2024学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 17:17:27 | ||
图片预览


文档简介
2023-2024学年人教版九年级数学上册《第23章旋转》
解答题题型分类专题训练(附答案)
一、作图题
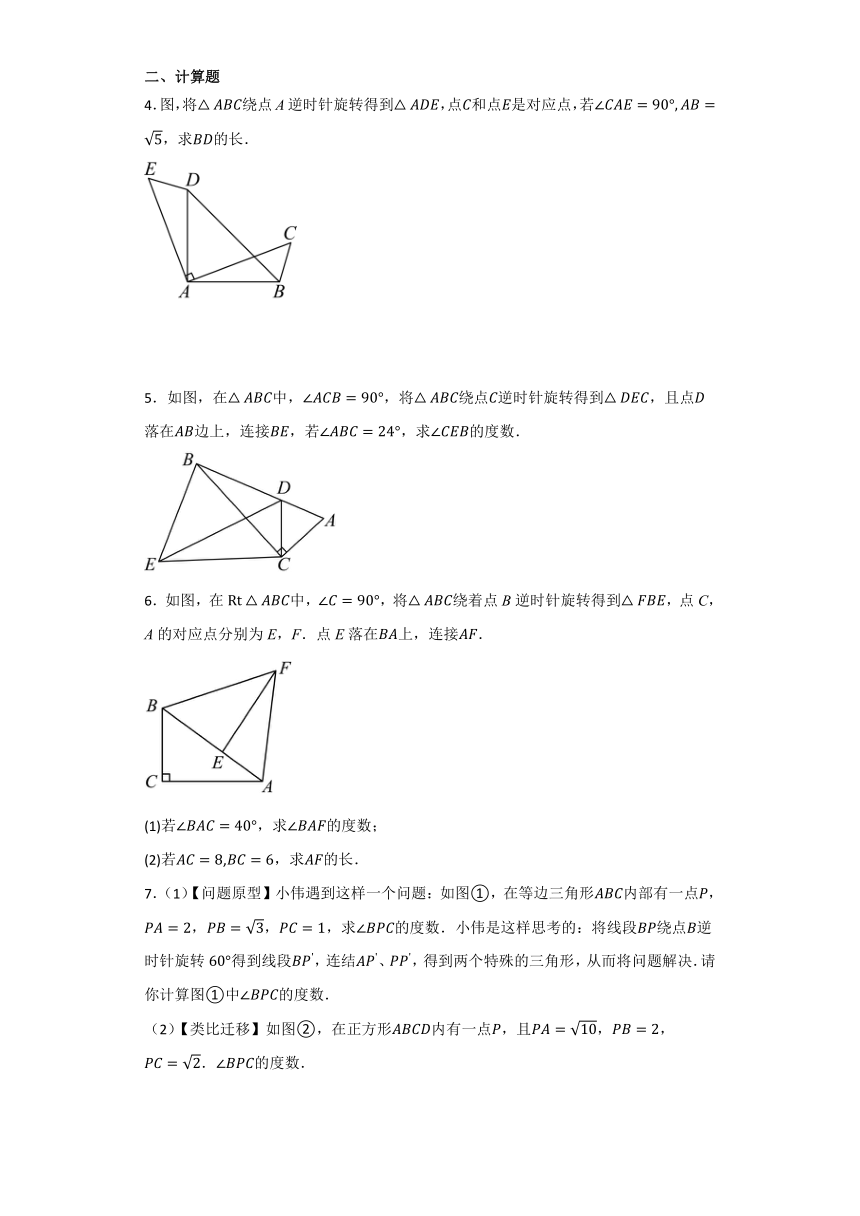
1.如图,三个顶点的坐标分别为,,.画出关于原点成中心对称的,并写出点、的坐标.
2.如图,在边长为1的正方形网格中建立平面直角坐标系,的三个顶点均在格点上.
(1)画出关于原点对称的;
(2)画出绕点逆时针旋转得到的,并写出点的坐标;
(3)若点为轴上一点,则的最小值为____________.
3.如图,是等边三角形,点E是边上的动点,将线段绕点E顺时针方向旋转得到线段,连接.
【问题解决】
(1)在图中画出线段、;
【问题探究】
(2)试探究的大小;
【拓展延伸】
(3)若等边三角形的边长为1,在点E从点B到点C的运动过程中,试探究点F的运动路径并求出其长度.
二、计算题
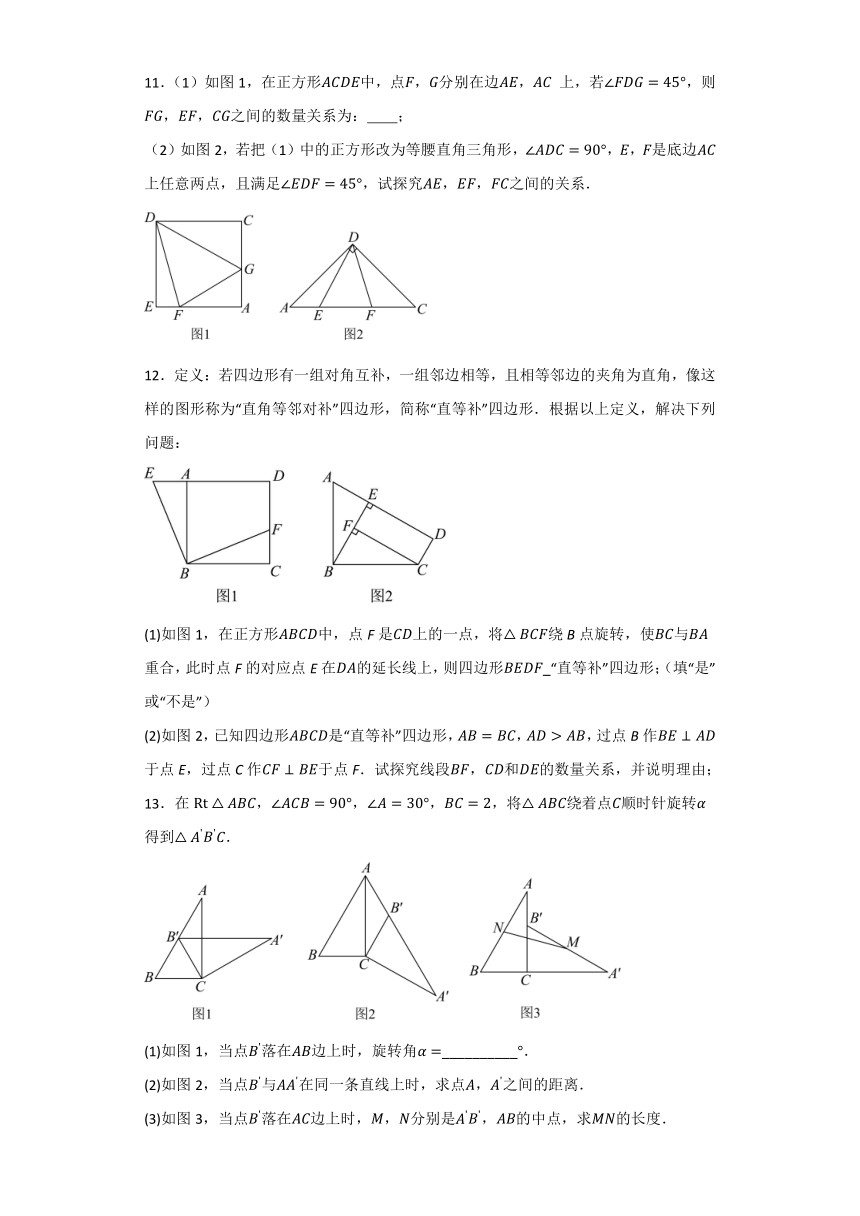
4.图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
5.如图,在中,,将绕点逆时针旋转得到,且点落在边上,连接,若,求的度数.
6.如图,在中,,将绕着点B逆时针旋转得到,点C,A的对应点分别为E,F.点E落在上,连接.
(1)若,求的度数;
(2)若,,求的长.
7.(1)【问题原型】小伟遇到这样一个问题:如图①,在等边三角形内部有一点,,,,求的度数.小伟是这样思考的:将线段绕点逆时针旋转得到线段,连结、,得到两个特殊的三角形,从而将问题解决.请你计算图①中的度数.
(2)【类比迁移】如图②,在正方形内有一点,且,,.的度数.
8.(1)数学兴趣小组同学将制作的和摆放成如图①所示的位置,且,,则AD和BE的数量关系为______;
(2)如图②,在中,,将线段CA绕点C顺时针旋转(),得到线段CD,连接AD、BD.小组同学发现无论为何值,的大小不变,请你计算这个定值,并写出计算过程;
(3)在第(2)问的基础上,在图③中作的平分线CE交BD于点F,交DA的延长线于点E,连接BE.用等式表示线段AD、CE、BE之间的数量关系;并证明.
三、问答题
9.如图,中,,,,逆时针旋转一定角度后与重合,且点恰好成为的中点.求出的度数和的长.
10.如图,在中,,以为边作等边三角形,把绕着点按顺时针方向旋转后得到,若,.求:
(1)的度数;
(2)的长.
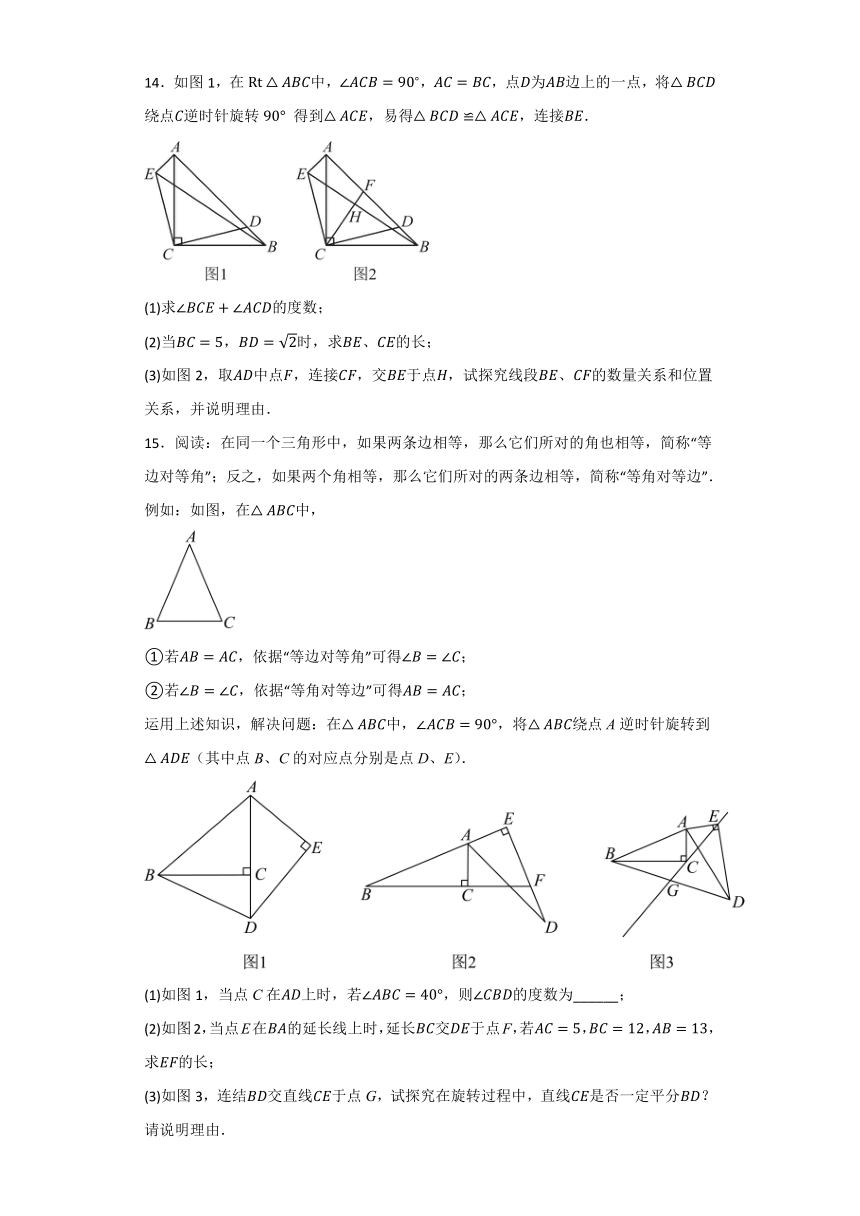
11.(1)如图1,在正方形中,点,分别在边, 上,若,则,,之间的数量关系为: ;
(2)如图2,若把(1)中的正方形改为等腰直角三角形,,,是底边上任意两点,且满足,试探究,,之间的关系.
12.定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:
(1)如图1,在正方形中,点F是上的一点,将绕B点旋转,使与重合,此时点F的对应点E在的延长线上,则四边形 “直等补”四边形;(填“是”或“不是”)
(2)如图2,已知四边形是“直等补”四边形,,,过点B作于点E,过点C作于点F.试探究线段,和的数量关系,并说明理由;
13.在,,,,将绕着点顺时针旋转得到.
(1)如图1,当点落在边上时,旋转角__________.
(2)如图2,当点与在同一条直线上时,求点,之间的距离.
(3)如图3,当点落在边上时,,分别是,的中点,求的长度.
14.如图1,在中,,,点为边上的一点,将绕点逆时针旋转 得到,易得,连接.
(1)求的度数;
(2)当,时,求、的长;
(3)如图2,取中点,连接,交于点,试探究线段、的数量关系和位置关系,并说明理由.
15.阅读:在同一个三角形中,如果两条边相等,那么它们所对的角也相等,简称“等边对等角”;反之,如果两个角相等,那么它们所对的两条边相等,简称“等角对等边”.
例如:如图,在中,
①若,依据“等边对等角”可得;
②若,依据“等角对等边”可得;
运用上述知识,解决问题:在中,,将绕点A逆时针旋转到(其中点B、C的对应点分别是点D、E).
(1)如图1,当点C在上时,若,则的度数为______;
(2)如图2,当点E在的延长线上时,延长交于点F,若,,,求的长;
(3)如图3,连结交直线于点G,试探究在旋转过程中,直线是否一定平分?请说明理由.
四、证明题
16.如图,过等边的顶点A作的垂线l,点P为l上点(不与点A重合),连接,将线段绕点C逆时针方向旋转得到线段,连接.
(1)求证:;
(2)连接并延长交直线于点D,若.
①试猜想和的数量关系,并证明;
②若,求的长.
17.如图1,在中,,D、E是边上的两点,且满足,以点B为旋转中心,将按逆时针方向旋转得到,连接.
(1)求证:;
(2)如图2,若,其他条件不变,探究之间的关系,并证明.
18.点分别是等边三角形的边和上的点,且,连接.
(1)如图1,若,将绕着点顺时针旋转,得到,连接和.求证:
①为等边三角形;
②.
(2)如图2,若,设为的中点,连接,求.
19.(1)【探究】如图1,正方形中,、分别在边上,且.我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图1,将绕点A顺时针旋转,点与点重合,得到,连接.
求证:.
(2)【拓展】如图2,在四边形中,cm,,, 以为顶点的,、与、边分别交于、两点且,求五边形的周长.
20.我们定义:如图1,在中,把绕点A顺时针旋转得到,把绕点A逆时针旋转得到,连接,当时,我们称是的“旋补三角形”,边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.
【阅读材料】(1)如图2,在中,若,.求边上的中线的取值范围.是这样思考的:延长至E.使,连结,利用全等将边转化到,在△中利用三角形三边关系即可求出中线的取值范围,则中线的取值范围是______;
【问题探索】(2)如图1,是的“旋补三角形”,是的“旋补中线”,请仿照上面材料中的方法,探索图1中与的数量关系,并给予证明;
【拓展运用】(3)如图3,当时,是的“旋补三角形”,,垂足为点E,的反向延长线交于点D,若,,试求解的取值范围.
参考答案
1.解:如图所示,即为所求,
点,的坐标分别为,.
2.解:(1)如图,即为所求;
(2)如图,即为所求, .
(3)作点关于轴的对称点',连接,交轴于点,连接,
则的最小值为
故答案为:.
3.(1)解:根据旋转的性质得,
如图,线段、即为所求.
(2)在上截取,连接,
∵是等边三角形,线段绕点E顺时针方向旋转得到线段,
,,
,,
,
,,
,
,
是等边三角形,
,
,
,
,
为等边三角形,
,
.
(3)是等边三角形,
,
,
延长至H,
,
,
∴点F在的平分线上,
∴点F运动路径在外角的平分线上,起点为点C,运动路径长度为.
4.解:∵将绕点A逆时针旋转得到,点和点是对应点,
∴,,
.
5.解:∵,,
∴.
由旋转得,
∴,
∴,
∴,
∵,
∴.
6.解:(1)在中,,,
∴,
∵将绕着点B逆时针旋转得到,
∴,,
∴;
(2)∵,,,
∴,
∵将绕着点B逆时针旋转得到,
∴,,,
∴,
∵,
∴在中,.
7.解:(1)【问题原型】将线段绕点逆时针旋转得到线段,连结、,
∴,
∴,,,,
∴是等边三角形,
∴,,
∵,
∴是直角三角形,,
∴,
∴;
(2)【类比迁移】如图,将绕点逆时针旋转,得到,
∴,
∴,,,,
∴是等腰直角三角形,
∴,,
∵,
∴是直角三角形,,
∴,
∴;
8.解:(1)AD=BE,理由如下:
∵在和中,,
∴∠ACB=∠DCE=90°,
∴∠DCE-∠DCB=∠ACB-∠DCB,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2),过程如下:
由旋转的性质可得,
∵AC=BC,
∴AC=BC=CD,
∴,
∵在中,,
∴,
∴,
∴;
(3),理由如下:
如图所示,将△ACE绕点C旋转90度得到△BCM,设,
由(2)得BC=CD,
∴∠EAC=∠MBC,∠ECM=90°,EC=CM,AE=BM,
∵CE平分∠BCD,
∴CE垂直平分BD,
∴BE=DE,∠EFD=∠EFB=90°,BF=DF,
∵EF=EF,
∴△BFE≌△DFE(SAS)
∵∠ADB=45°,
∴∠EBF=∠EDF=∠BEF=∠DEF=45°,
∴EF=BF=DF,∠BED=90°,
∵∠BEA+∠EAC+∠ACB+∠EBC=360°,
∴∠EAC+∠EBC=180°,
∴∠EBC+∠MBC=180°,即E、B、M三点共线,
在中,由勾股定理得:,
在中,由勾股定理得:,
∴,
∴,
∴,
∴;
9.解:由图可知,旋转中心为点A,
∵,,
∴,
∵逆时针旋转一定角度后与重合,
∴,,,
∴,
∵点C恰好成为的中点,
∴,
∴.
10.(1)解:由题知:,
∴,,
∴,,
∵,,
∴,
∴,
∴,
∴、、在一条直线上,
∴是等边三角形,
∴.
(2)解:∵、、在一条直线上,
∴,
∵绕着点按顺时针方向旋转后得到,
∴,
∴.
11.解:(1),理由如下:
如图,以点为旋转中心,将顺时针旋转得,
,
,,,
四边形是正方形,
,,
,
,
,
在和中,
,
,
,
;
;
故答案为:;
(2),理由如下:
是等腰直角三角形,,
,
如图,以点为旋转中心,将顺时针旋转得,
,
,,,,
,
,
,
在和中,
,
,
,
,
,
.
12.解:(1)∵将绕B点旋转,使与重合,此时点F的对应点E在的延长线上,
∴,,
∵四边形是正方形,
∴,
∴,
∴,即,
∴,
∵,,
∴四边形是“直等补”四边形.
故答案为:是
(2)∵四边形是“直等补”四边形,,,
∴,,
∴,
∵,,
∴,
∴四边形是矩形,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴.
13.(1)解:∵,,
∴,
∵将绕着点顺时针旋转得到,
∴,
∴为等边三角形,
∴,
∴,
故答案为:;
(2)由旋转可知,,,,,
∴,
∴,
∴,
∴,
∴,
∵,,,
∴,,
∴,
∴,
即点,之间的距离为;
(3)连接,
∵,分别是,的中点,
∴,,
∵,
∴,
∵,,
∴,,
∴,
∴.
14.(1)证明:由旋转可知,
∵,
∴;
(2)∵,,
∴,.
由旋转,可知,,
∴,
∴.
过作于,
∴,
∵,
∴,
∴,
在中:,
∴,
∴,
∴,
∴,
∴;
(3)与有如下关系:,.理由如下:
如图,延长到点,使,
∵点为的中点,
∴.
∵,
∴.
∴,,
∴,
∴.
由(1)知,
∴.
又由旋转知,
∴,
∴,,
∴,
∴.
15.解:(1)∵,,
∴.
∵由旋转的性质得,
∴.
∴,
∴.
故答案为:;
(2)如图2,连接,由旋转性质得,,
∴,
∴和是直角三角形,
在和中,,(公共边)
∴,
∴,
设,
∵,,,
∴,
在中,,得
解得,即
(3)如图3,直线一定平分,
理由如下:
过点B作与直线交于点H,
∴
由旋转性质得,,,
∴,,,
∴,
∴,
∴,
∴.
在和中,,,,
∴,
∴,
∴直线一定平分.
16.(1)证明:在等边中,,,
由旋转可得,,
∴,
∴
即,
∴
∴
(2)①猜想:.
证明:连接,如图:
由旋转,得,,
∴是等边三角形
∵,
∴,
∴是的垂直平分线
∵点B在上,
∴;
②解:由(1)得
∴,,
∴
∵,
∴,
∴
∴.
在中,
∴,
∴.
∵,,
∴,
∵,
∴,
∴
∴,
答:的长为
17.(1)证明:∵,
∴,
由旋转得,
∴,,
∴,
∴,
∵,
∴,
∴;
(2)解:,证明如下:
∵,
∴,
∵,
∴,
由旋转,得,,
∴,
∴,
由(1)得,
∴.
18.(1)①证明:绕着点顺时针旋转,
.
为等边三角形.
②∵等边三角形,
∴,
如图,过作,则,
∴为等边三角形,
∴,
∴.
∵为等边三角形,
∴,
∴,
又,
∴,
.
即.
(2)解:延长至,使得,连接和,
∵是的中点,
∴,
又,
∴,
∴.
,
为等边三角形.
.
过点作,则:,
∴,
19.解:(1)【探究】证明:∵将绕点顺时针旋转,点与点重合,得到,连接.
∴,,,,
∵四边形.是正方形,
∴,,
∴,
∴点、、三点共线,
∴,
∵,
∴,
在和中,
,
∴,
∴,
;
(2)【拓展】将绕点顺时针旋转,使点与点重合,得到,
,,,,,
,
,
,
,
,
,
,
∴五边形的周长 ,
∴五边形的周长.
20.解:(1)∵是中线,
∴,
∵,,
∴,
∴,而,
∴,,,
由三角形三边关系可得:,即,
∴,
(2);理由如下:
如图1,延长至点E使,连接,
∵是的“旋补中线”,
∴是的中线,即,
又∵,
∴,
∴,,
∵,
∴,
∵是的“旋补中线”,
∴,
∵,,
∴,
∵,,
∴,
∴.
(3)如图,作于H,作交延长线于F,
∵,
∴,
∴,
∵,即,
∴,
∴,
又∵,
∴,
∴,
又∵,,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴是的中线,
∵,,
结合(1)的结论可得:,即.
解答题题型分类专题训练(附答案)
一、作图题
1.如图,三个顶点的坐标分别为,,.画出关于原点成中心对称的,并写出点、的坐标.
2.如图,在边长为1的正方形网格中建立平面直角坐标系,的三个顶点均在格点上.
(1)画出关于原点对称的;
(2)画出绕点逆时针旋转得到的,并写出点的坐标;
(3)若点为轴上一点,则的最小值为____________.
3.如图,是等边三角形,点E是边上的动点,将线段绕点E顺时针方向旋转得到线段,连接.
【问题解决】
(1)在图中画出线段、;
【问题探究】
(2)试探究的大小;
【拓展延伸】
(3)若等边三角形的边长为1,在点E从点B到点C的运动过程中,试探究点F的运动路径并求出其长度.
二、计算题
4.图,将绕点A逆时针旋转得到,点和点是对应点,若,求的长.
5.如图,在中,,将绕点逆时针旋转得到,且点落在边上,连接,若,求的度数.
6.如图,在中,,将绕着点B逆时针旋转得到,点C,A的对应点分别为E,F.点E落在上,连接.
(1)若,求的度数;
(2)若,,求的长.
7.(1)【问题原型】小伟遇到这样一个问题:如图①,在等边三角形内部有一点,,,,求的度数.小伟是这样思考的:将线段绕点逆时针旋转得到线段,连结、,得到两个特殊的三角形,从而将问题解决.请你计算图①中的度数.
(2)【类比迁移】如图②,在正方形内有一点,且,,.的度数.
8.(1)数学兴趣小组同学将制作的和摆放成如图①所示的位置,且,,则AD和BE的数量关系为______;
(2)如图②,在中,,将线段CA绕点C顺时针旋转(),得到线段CD,连接AD、BD.小组同学发现无论为何值,的大小不变,请你计算这个定值,并写出计算过程;
(3)在第(2)问的基础上,在图③中作的平分线CE交BD于点F,交DA的延长线于点E,连接BE.用等式表示线段AD、CE、BE之间的数量关系;并证明.
三、问答题
9.如图,中,,,,逆时针旋转一定角度后与重合,且点恰好成为的中点.求出的度数和的长.
10.如图,在中,,以为边作等边三角形,把绕着点按顺时针方向旋转后得到,若,.求:
(1)的度数;
(2)的长.
11.(1)如图1,在正方形中,点,分别在边, 上,若,则,,之间的数量关系为: ;
(2)如图2,若把(1)中的正方形改为等腰直角三角形,,,是底边上任意两点,且满足,试探究,,之间的关系.
12.定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:
(1)如图1,在正方形中,点F是上的一点,将绕B点旋转,使与重合,此时点F的对应点E在的延长线上,则四边形 “直等补”四边形;(填“是”或“不是”)
(2)如图2,已知四边形是“直等补”四边形,,,过点B作于点E,过点C作于点F.试探究线段,和的数量关系,并说明理由;
13.在,,,,将绕着点顺时针旋转得到.
(1)如图1,当点落在边上时,旋转角__________.
(2)如图2,当点与在同一条直线上时,求点,之间的距离.
(3)如图3,当点落在边上时,,分别是,的中点,求的长度.
14.如图1,在中,,,点为边上的一点,将绕点逆时针旋转 得到,易得,连接.
(1)求的度数;
(2)当,时,求、的长;
(3)如图2,取中点,连接,交于点,试探究线段、的数量关系和位置关系,并说明理由.
15.阅读:在同一个三角形中,如果两条边相等,那么它们所对的角也相等,简称“等边对等角”;反之,如果两个角相等,那么它们所对的两条边相等,简称“等角对等边”.
例如:如图,在中,
①若,依据“等边对等角”可得;
②若,依据“等角对等边”可得;
运用上述知识,解决问题:在中,,将绕点A逆时针旋转到(其中点B、C的对应点分别是点D、E).
(1)如图1,当点C在上时,若,则的度数为______;
(2)如图2,当点E在的延长线上时,延长交于点F,若,,,求的长;
(3)如图3,连结交直线于点G,试探究在旋转过程中,直线是否一定平分?请说明理由.
四、证明题
16.如图,过等边的顶点A作的垂线l,点P为l上点(不与点A重合),连接,将线段绕点C逆时针方向旋转得到线段,连接.
(1)求证:;
(2)连接并延长交直线于点D,若.
①试猜想和的数量关系,并证明;
②若,求的长.
17.如图1,在中,,D、E是边上的两点,且满足,以点B为旋转中心,将按逆时针方向旋转得到,连接.
(1)求证:;
(2)如图2,若,其他条件不变,探究之间的关系,并证明.
18.点分别是等边三角形的边和上的点,且,连接.
(1)如图1,若,将绕着点顺时针旋转,得到,连接和.求证:
①为等边三角形;
②.
(2)如图2,若,设为的中点,连接,求.
19.(1)【探究】如图1,正方形中,、分别在边上,且.我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法.如图1,将绕点A顺时针旋转,点与点重合,得到,连接.
求证:.
(2)【拓展】如图2,在四边形中,cm,,, 以为顶点的,、与、边分别交于、两点且,求五边形的周长.
20.我们定义:如图1,在中,把绕点A顺时针旋转得到,把绕点A逆时针旋转得到,连接,当时,我们称是的“旋补三角形”,边上的中线叫做的“旋补中线”,点A叫做“旋补中心”.
【阅读材料】(1)如图2,在中,若,.求边上的中线的取值范围.是这样思考的:延长至E.使,连结,利用全等将边转化到,在△中利用三角形三边关系即可求出中线的取值范围,则中线的取值范围是______;
【问题探索】(2)如图1,是的“旋补三角形”,是的“旋补中线”,请仿照上面材料中的方法,探索图1中与的数量关系,并给予证明;
【拓展运用】(3)如图3,当时,是的“旋补三角形”,,垂足为点E,的反向延长线交于点D,若,,试求解的取值范围.
参考答案
1.解:如图所示,即为所求,
点,的坐标分别为,.
2.解:(1)如图,即为所求;
(2)如图,即为所求, .
(3)作点关于轴的对称点',连接,交轴于点,连接,
则的最小值为
故答案为:.
3.(1)解:根据旋转的性质得,
如图,线段、即为所求.
(2)在上截取,连接,
∵是等边三角形,线段绕点E顺时针方向旋转得到线段,
,,
,,
,
,,
,
,
是等边三角形,
,
,
,
,
为等边三角形,
,
.
(3)是等边三角形,
,
,
延长至H,
,
,
∴点F在的平分线上,
∴点F运动路径在外角的平分线上,起点为点C,运动路径长度为.
4.解:∵将绕点A逆时针旋转得到,点和点是对应点,
∴,,
.
5.解:∵,,
∴.
由旋转得,
∴,
∴,
∴,
∵,
∴.
6.解:(1)在中,,,
∴,
∵将绕着点B逆时针旋转得到,
∴,,
∴;
(2)∵,,,
∴,
∵将绕着点B逆时针旋转得到,
∴,,,
∴,
∵,
∴在中,.
7.解:(1)【问题原型】将线段绕点逆时针旋转得到线段,连结、,
∴,
∴,,,,
∴是等边三角形,
∴,,
∵,
∴是直角三角形,,
∴,
∴;
(2)【类比迁移】如图,将绕点逆时针旋转,得到,
∴,
∴,,,,
∴是等腰直角三角形,
∴,,
∵,
∴是直角三角形,,
∴,
∴;
8.解:(1)AD=BE,理由如下:
∵在和中,,
∴∠ACB=∠DCE=90°,
∴∠DCE-∠DCB=∠ACB-∠DCB,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE;
(2),过程如下:
由旋转的性质可得,
∵AC=BC,
∴AC=BC=CD,
∴,
∵在中,,
∴,
∴,
∴;
(3),理由如下:
如图所示,将△ACE绕点C旋转90度得到△BCM,设,
由(2)得BC=CD,
∴∠EAC=∠MBC,∠ECM=90°,EC=CM,AE=BM,
∵CE平分∠BCD,
∴CE垂直平分BD,
∴BE=DE,∠EFD=∠EFB=90°,BF=DF,
∵EF=EF,
∴△BFE≌△DFE(SAS)
∵∠ADB=45°,
∴∠EBF=∠EDF=∠BEF=∠DEF=45°,
∴EF=BF=DF,∠BED=90°,
∵∠BEA+∠EAC+∠ACB+∠EBC=360°,
∴∠EAC+∠EBC=180°,
∴∠EBC+∠MBC=180°,即E、B、M三点共线,
在中,由勾股定理得:,
在中,由勾股定理得:,
∴,
∴,
∴,
∴;
9.解:由图可知,旋转中心为点A,
∵,,
∴,
∵逆时针旋转一定角度后与重合,
∴,,,
∴,
∵点C恰好成为的中点,
∴,
∴.
10.(1)解:由题知:,
∴,,
∴,,
∵,,
∴,
∴,
∴,
∴、、在一条直线上,
∴是等边三角形,
∴.
(2)解:∵、、在一条直线上,
∴,
∵绕着点按顺时针方向旋转后得到,
∴,
∴.
11.解:(1),理由如下:
如图,以点为旋转中心,将顺时针旋转得,
,
,,,
四边形是正方形,
,,
,
,
,
在和中,
,
,
,
;
;
故答案为:;
(2),理由如下:
是等腰直角三角形,,
,
如图,以点为旋转中心,将顺时针旋转得,
,
,,,,
,
,
,
在和中,
,
,
,
,
,
.
12.解:(1)∵将绕B点旋转,使与重合,此时点F的对应点E在的延长线上,
∴,,
∵四边形是正方形,
∴,
∴,
∴,即,
∴,
∵,,
∴四边形是“直等补”四边形.
故答案为:是
(2)∵四边形是“直等补”四边形,,,
∴,,
∴,
∵,,
∴,
∴四边形是矩形,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴.
13.(1)解:∵,,
∴,
∵将绕着点顺时针旋转得到,
∴,
∴为等边三角形,
∴,
∴,
故答案为:;
(2)由旋转可知,,,,,
∴,
∴,
∴,
∴,
∴,
∵,,,
∴,,
∴,
∴,
即点,之间的距离为;
(3)连接,
∵,分别是,的中点,
∴,,
∵,
∴,
∵,,
∴,,
∴,
∴.
14.(1)证明:由旋转可知,
∵,
∴;
(2)∵,,
∴,.
由旋转,可知,,
∴,
∴.
过作于,
∴,
∵,
∴,
∴,
在中:,
∴,
∴,
∴,
∴,
∴;
(3)与有如下关系:,.理由如下:
如图,延长到点,使,
∵点为的中点,
∴.
∵,
∴.
∴,,
∴,
∴.
由(1)知,
∴.
又由旋转知,
∴,
∴,,
∴,
∴.
15.解:(1)∵,,
∴.
∵由旋转的性质得,
∴.
∴,
∴.
故答案为:;
(2)如图2,连接,由旋转性质得,,
∴,
∴和是直角三角形,
在和中,,(公共边)
∴,
∴,
设,
∵,,,
∴,
在中,,得
解得,即
(3)如图3,直线一定平分,
理由如下:
过点B作与直线交于点H,
∴
由旋转性质得,,,
∴,,,
∴,
∴,
∴,
∴.
在和中,,,,
∴,
∴,
∴直线一定平分.
16.(1)证明:在等边中,,,
由旋转可得,,
∴,
∴
即,
∴
∴
(2)①猜想:.
证明:连接,如图:
由旋转,得,,
∴是等边三角形
∵,
∴,
∴是的垂直平分线
∵点B在上,
∴;
②解:由(1)得
∴,,
∴
∵,
∴,
∴
∴.
在中,
∴,
∴.
∵,,
∴,
∵,
∴,
∴
∴,
答:的长为
17.(1)证明:∵,
∴,
由旋转得,
∴,,
∴,
∴,
∵,
∴,
∴;
(2)解:,证明如下:
∵,
∴,
∵,
∴,
由旋转,得,,
∴,
∴,
由(1)得,
∴.
18.(1)①证明:绕着点顺时针旋转,
.
为等边三角形.
②∵等边三角形,
∴,
如图,过作,则,
∴为等边三角形,
∴,
∴.
∵为等边三角形,
∴,
∴,
又,
∴,
.
即.
(2)解:延长至,使得,连接和,
∵是的中点,
∴,
又,
∴,
∴.
,
为等边三角形.
.
过点作,则:,
∴,
19.解:(1)【探究】证明:∵将绕点顺时针旋转,点与点重合,得到,连接.
∴,,,,
∵四边形.是正方形,
∴,,
∴,
∴点、、三点共线,
∴,
∵,
∴,
在和中,
,
∴,
∴,
;
(2)【拓展】将绕点顺时针旋转,使点与点重合,得到,
,,,,,
,
,
,
,
,
,
,
∴五边形的周长 ,
∴五边形的周长.
20.解:(1)∵是中线,
∴,
∵,,
∴,
∴,而,
∴,,,
由三角形三边关系可得:,即,
∴,
(2);理由如下:
如图1,延长至点E使,连接,
∵是的“旋补中线”,
∴是的中线,即,
又∵,
∴,
∴,,
∵,
∴,
∵是的“旋补中线”,
∴,
∵,,
∴,
∵,,
∴,
∴.
(3)如图,作于H,作交延长线于F,
∵,
∴,
∴,
∵,即,
∴,
∴,
又∵,
∴,
∴,
又∵,,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴是的中线,
∵,,
结合(1)的结论可得:,即.
同课章节目录
