2.2 探索直线平行的条件(第2课时)同步课件(共34张PPT)
文档属性
| 名称 | 2.2 探索直线平行的条件(第2课时)同步课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览





文档简介
(共34张PPT)
2.2 探索直线平行的条件
第2课时
学习目标
1)理解并掌握内错角、同旁内角的概念,能够判定内错角、同旁内角。
2)能够运用内错角相等、同旁内角互补判定两直线平行。
重点
理解并掌握内错角、同旁内角的概念,能够判定内错角、同旁内角。
难点
能够运用内错角相等、同旁内角互补判定两直线平行。
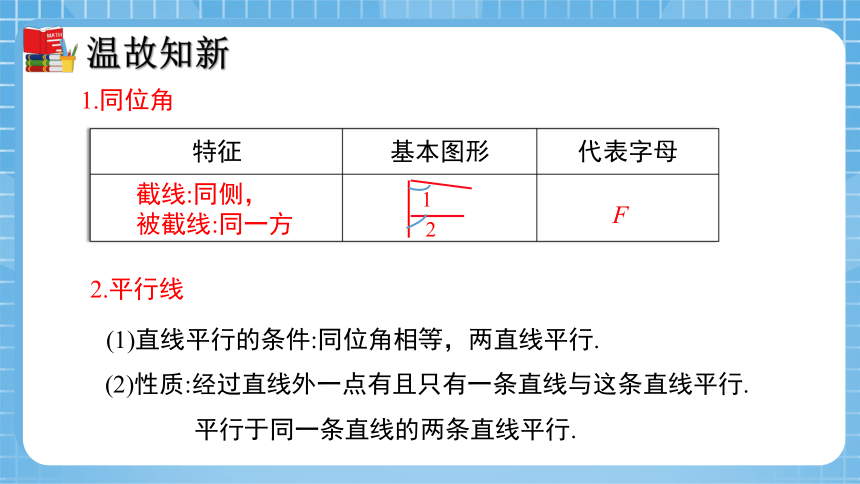
特征 基本图形 代表字母
F
截线:同侧,
被截线:同一方
1
2
1.同位角
2.平行线
(1)直线平行的条件:同位角相等,两直线平行.
平行于同一条直线的两条直线平行.
(2)性质:经过直线外一点有且只有一条直线与这条直线平行.
还有其他的判定方法吗?
3.判断两直线平行的方法:
方法1:定义(很少用)
方法2:同位角相等,两直线平行(经常用);
方法3:平行于同一条直线的两直线平行(偶尔用)
小明身边只有一个量角器, 他通过测量某些角的大小就能知道这个画板的上、 下边缘是否平行, 你知道他是怎样做的吗?
A
C
B
D
E
F
1
2
3
4
5
6
7
8
问题1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
两条直线被第三条直线所截,位于截线两侧,被截线之间的两个角,叫做内错角.
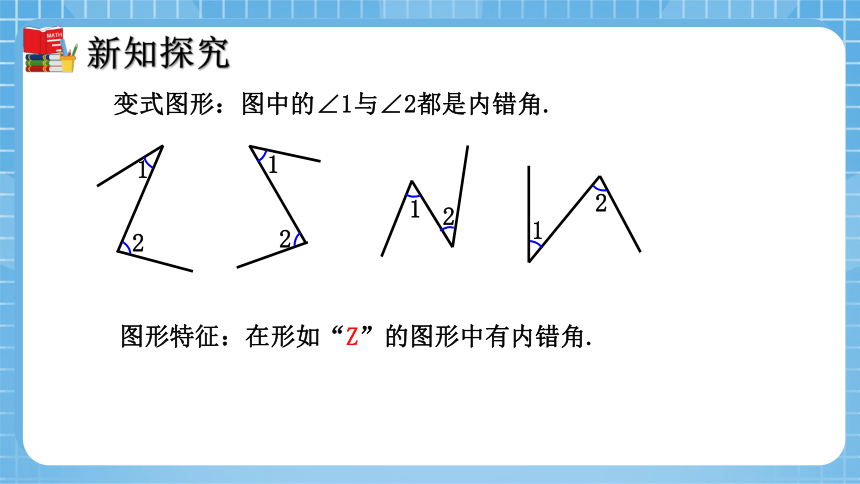
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
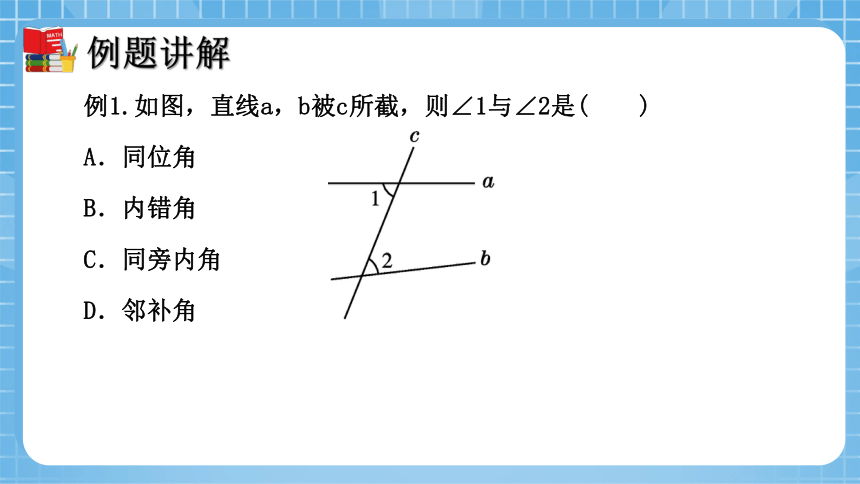
例1.如图,直线a,b被c所截,则∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
C
A
D
B
l
1
2
3
4
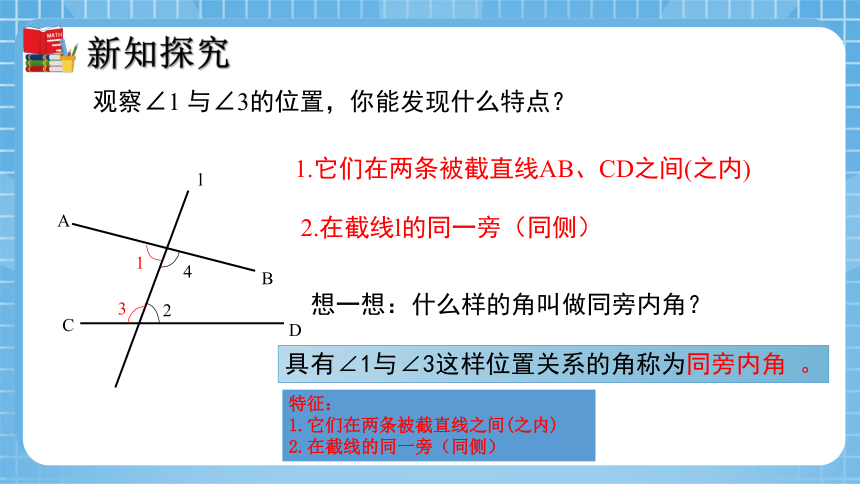
观察∠1 与∠3的位置,你能发现什么特点?
1.它们在两条被截直线AB、CD之间(之内)
2.在截线l的同一旁(同侧)
具有∠1与∠3这样位置关系的角称为同旁内角 。
想一想:什么样的角叫做同旁内角?
特征:
1.它们在两条被截直线之间(之内)
2.在截线的同一旁(同侧)
C
A
D
B
l
1
2
3
4
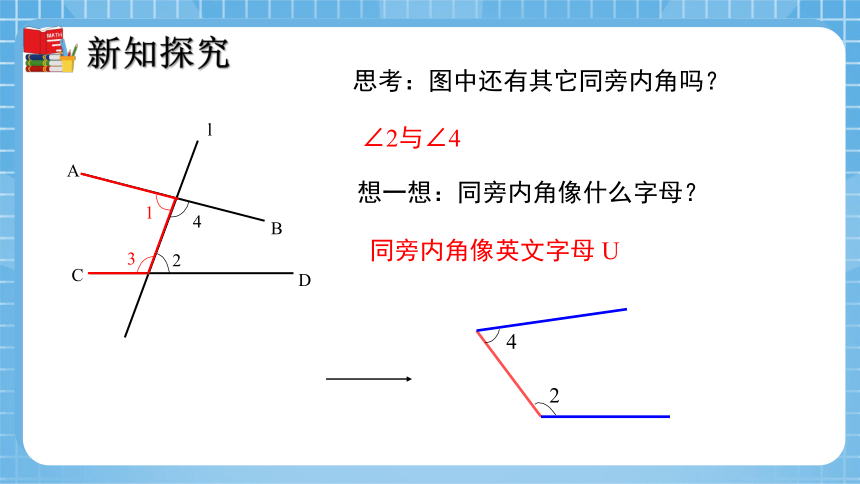
想一想:同旁内角像什么字母?
同旁内角像英文字母 U
思考:图中还有其它同旁内角吗?
∠2与∠4
4
2
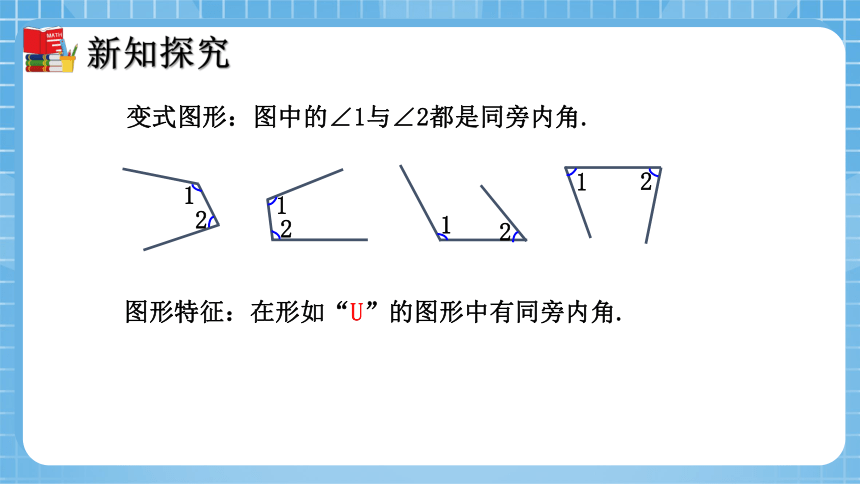
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
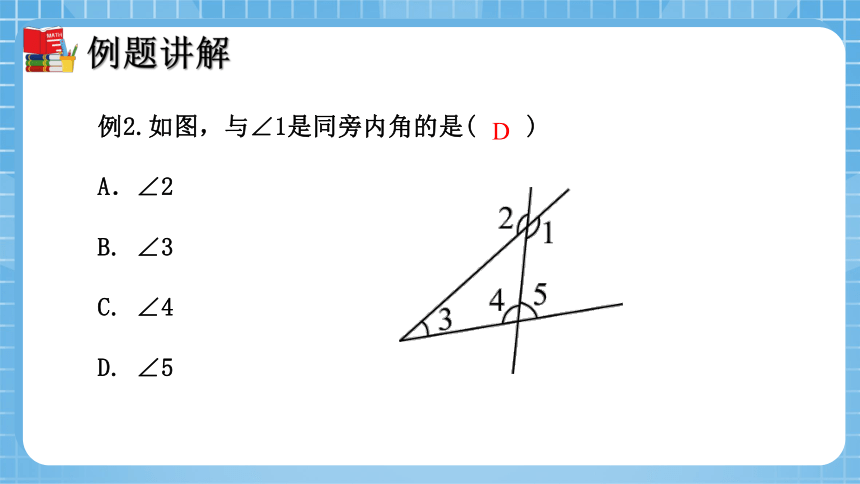
例2.如图,与∠1是同旁内角的是( )
A.∠2
B. ∠3
C. ∠4
D. ∠5
D
(1)内错角满足什么关系时,两直线平行?为什么?
(2)同旁内角满足什么关系时,两直线平行?为什么?
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a∥b.
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b.(内错角相等,两直线平行)
几何语言:
2
b
a
1
c
平行线判定方法2:
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
平行线判定方法3:
简单说成:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°,(已知)
∴a∥b.(同旁内角互补,两直线平行)
2
b
a
1
c
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简称为: 内错角相等, 两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简称为: 同旁内角互补, 两直线平行.
如图,三个相同的三角尺拼接成一个图形,请找出图中的一组平行线,并说明你的理由.
B
C
A
E
D
BC与AE是平行的.因为∠BCA与∠EAC是内错角,而且又相等.
B
C
A
E
D
你能看懂她的意思吗?
再找到另一组平行线,说说你的理由.
B
C
A
E
D
能.她由∠BCA=∠EAC,推出BC∥AE,理由是“内错角相等,两直线平行”.
AB∥EC.理由:因为∠BAC=∠ECA=90°,根据“内错角相等,两直线平行”,可知AB∥EC.
例3.如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
解:因为∠1=∠AOD(对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
1. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
2.如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出的是( )
A.①② B.①③
C.②③ D.②④
【详解】①∵∠1=∠2,∴AB∥CD;
②∵∠3=∠4,∴AD∥BC;
③∵∠B=∠DCE,∴AB∥CD;
④∵∠B+∠BAD=180°,∴AD∥BC;∴能得到AB∥CD的条件是①③.故选择:B
4.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
5.如图,直线DE,BC被直线AB所截.
∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.
6.如图,已知CB平分∠ACD,且∠1=∠2,试说明:AB∥CD.
证明:∵CB平分∠ACD(已知)
∴∠1=∠BCD(平分定义)
又∠1=∠2(已知)
∴∠2=∠BCD(等量代换)
∴AB∥CD(内错角相等,两直线平行)
7.如图所示,点E在BC的延长线上,下列条件中,①∠2=∠5;②∠3=∠4;③∠ACE+∠E=180°;④∠B=∠3,能判断AC//DE的有_________________.
【详解】解:①根据∠2=∠5,可得AC∥DE;
②根据∠3=∠4,可得AD∥CE;
③根据∠ACE+∠E=180°,可得AC∥DE;
④根据∠B=∠3,可得AB∥DC.
∴能判断AC∥DE的有①③,
故选:C.
8. 如图,若∠1=∠2,∠3+∠4=180°,则直线a与c平行吗?为什么?
解:a∥c.理由如下:
∵∠1=∠2(已知)
∴a∥b(内错角相等,两直线平行)
∵∠3+∠4=180°(已知)
∴b∥c(同旁内角互补,两直线平行)
∴a∥c(平行于同一直线的两直线平行)
9.已知:如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1)如果∠2=∠3,那么____________.(____________,____________)
(2)如果∠2=∠5,那么____________.(____________,____________)
(3)如果∠2+∠1=180°,那么____________.(____________,____________)
(4)如果∠5=∠3,那么____________.(____________,____________)
【详解】(1)如果∠2=∠3,那么EF∥DC.(内错角相等,两直线平行);
(2)如果∠2=∠5,那么EF∥AB.(同位角相等,两直线平行);
(3)如果∠2+∠1=180°,那么AD∥BC.(同旁内角互补,两直线平行);
(4)如果∠5=∠3,那么AB∥CD.(内错角相等,两直线平行.
文字叙述 符号语言 图形
相等 两直线平行 因为 (已知) 所以a∥b
________相等 两直线平行 因为 (已知) 所以a∥b _________互补 两直线平行 因为 (已知) 所以a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
习题2.4
第1、2题
2.2 探索直线平行的条件
第2课时
学习目标
1)理解并掌握内错角、同旁内角的概念,能够判定内错角、同旁内角。
2)能够运用内错角相等、同旁内角互补判定两直线平行。
重点
理解并掌握内错角、同旁内角的概念,能够判定内错角、同旁内角。
难点
能够运用内错角相等、同旁内角互补判定两直线平行。
特征 基本图形 代表字母
F
截线:同侧,
被截线:同一方
1
2
1.同位角
2.平行线
(1)直线平行的条件:同位角相等,两直线平行.
平行于同一条直线的两条直线平行.
(2)性质:经过直线外一点有且只有一条直线与这条直线平行.
还有其他的判定方法吗?
3.判断两直线平行的方法:
方法1:定义(很少用)
方法2:同位角相等,两直线平行(经常用);
方法3:平行于同一条直线的两直线平行(偶尔用)
小明身边只有一个量角器, 他通过测量某些角的大小就能知道这个画板的上、 下边缘是否平行, 你知道他是怎样做的吗?
A
C
B
D
E
F
1
2
3
4
5
6
7
8
问题1 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB、CD的之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
两条直线被第三条直线所截,位于截线两侧,被截线之间的两个角,叫做内错角.
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
例1.如图,直线a,b被c所截,则∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
C
A
D
B
l
1
2
3
4
观察∠1 与∠3的位置,你能发现什么特点?
1.它们在两条被截直线AB、CD之间(之内)
2.在截线l的同一旁(同侧)
具有∠1与∠3这样位置关系的角称为同旁内角 。
想一想:什么样的角叫做同旁内角?
特征:
1.它们在两条被截直线之间(之内)
2.在截线的同一旁(同侧)
C
A
D
B
l
1
2
3
4
想一想:同旁内角像什么字母?
同旁内角像英文字母 U
思考:图中还有其它同旁内角吗?
∠2与∠4
4
2
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
例2.如图,与∠1是同旁内角的是( )
A.∠2
B. ∠3
C. ∠4
D. ∠5
D
(1)内错角满足什么关系时,两直线平行?为什么?
(2)同旁内角满足什么关系时,两直线平行?为什么?
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
∵ ∠1=∠3
而∠2=∠3 (对顶角相等)
∴ ∠2=∠1(等量代换)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1=∠3,试说明a∥b.
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b.(内错角相等,两直线平行)
几何语言:
2
b
a
1
c
平行线判定方法2:
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢
∵ ∠1+∠3 =180°, ∠2+∠3 =180°
∴ ∠2=∠1(同角的补角相等)
∴ a∥b(同位角相等,两直线平行)
如图,已知∠1+∠3=180°,试说明a∥b.
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
平行线判定方法3:
简单说成:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°,(已知)
∴a∥b.(同旁内角互补,两直线平行)
2
b
a
1
c
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简称为: 内错角相等, 两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简称为: 同旁内角互补, 两直线平行.
如图,三个相同的三角尺拼接成一个图形,请找出图中的一组平行线,并说明你的理由.
B
C
A
E
D
BC与AE是平行的.因为∠BCA与∠EAC是内错角,而且又相等.
B
C
A
E
D
你能看懂她的意思吗?
再找到另一组平行线,说说你的理由.
B
C
A
E
D
能.她由∠BCA=∠EAC,推出BC∥AE,理由是“内错角相等,两直线平行”.
AB∥EC.理由:因为∠BAC=∠ECA=90°,根据“内错角相等,两直线平行”,可知AB∥EC.
例3.如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
解:因为∠1=∠AOD(对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD(同旁内角互补,两直线平行).
1. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
2.如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
3.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出的是( )
A.①② B.①③
C.②③ D.②④
【详解】①∵∠1=∠2,∴AB∥CD;
②∵∠3=∠4,∴AD∥BC;
③∵∠B=∠DCE,∴AB∥CD;
④∵∠B+∠BAD=180°,∴AD∥BC;∴能得到AB∥CD的条件是①③.故选择:B
4.如图,已知∠1= ∠3,AC平分∠DAB你能判断那两条直线平行?请说明理由?
2
3
A
B
C
D
)
)
1
(
5.如图,直线DE,BC被直线AB所截.
∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:∠1与∠2是内错角,∠1和∠3同旁内角,∠1和∠4是同旁内角.
6.如图,已知CB平分∠ACD,且∠1=∠2,试说明:AB∥CD.
证明:∵CB平分∠ACD(已知)
∴∠1=∠BCD(平分定义)
又∠1=∠2(已知)
∴∠2=∠BCD(等量代换)
∴AB∥CD(内错角相等,两直线平行)
7.如图所示,点E在BC的延长线上,下列条件中,①∠2=∠5;②∠3=∠4;③∠ACE+∠E=180°;④∠B=∠3,能判断AC//DE的有_________________.
【详解】解:①根据∠2=∠5,可得AC∥DE;
②根据∠3=∠4,可得AD∥CE;
③根据∠ACE+∠E=180°,可得AC∥DE;
④根据∠B=∠3,可得AB∥DC.
∴能判断AC∥DE的有①③,
故选:C.
8. 如图,若∠1=∠2,∠3+∠4=180°,则直线a与c平行吗?为什么?
解:a∥c.理由如下:
∵∠1=∠2(已知)
∴a∥b(内错角相等,两直线平行)
∵∠3+∠4=180°(已知)
∴b∥c(同旁内角互补,两直线平行)
∴a∥c(平行于同一直线的两直线平行)
9.已知:如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.
(1)如果∠2=∠3,那么____________.(____________,____________)
(2)如果∠2=∠5,那么____________.(____________,____________)
(3)如果∠2+∠1=180°,那么____________.(____________,____________)
(4)如果∠5=∠3,那么____________.(____________,____________)
【详解】(1)如果∠2=∠3,那么EF∥DC.(内错角相等,两直线平行);
(2)如果∠2=∠5,那么EF∥AB.(同位角相等,两直线平行);
(3)如果∠2+∠1=180°,那么AD∥BC.(同旁内角互补,两直线平行);
(4)如果∠5=∠3,那么AB∥CD.(内错角相等,两直线平行.
文字叙述 符号语言 图形
相等 两直线平行 因为 (已知) 所以a∥b
________相等 两直线平行 因为 (已知) 所以a∥b _________互补 两直线平行 因为 (已知) 所以a∥b 判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
习题2.4
第1、2题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
