华师大版七年级数学上3.1. 1《字母表示数》说课课件(共33张PPT)
文档属性
| 名称 | 华师大版七年级数学上3.1. 1《字母表示数》说课课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
§3.1 字母表示数
教材分析
教学过程
板书设计
——说 课 环 节——
教法学法
教材分析
所处的地位与作用:
本节课是在学生掌握了常见的数量关系、周长、面积计算等知识的基础上安排的,这些都是理解本单元所学知识的重要基础。本课内容看似浅显、平淡,但它是由具体的数和运算符号组成的式子过渡到含有字母的式子,使学生建立初步的符号感,是学生学习数学的一个转折点,也是认识过程上的一次飞跃。对提高学生的数学认知水平有着非常重要的作用。同时本单元知识又是学生进入代数知识学习的入门知识,是学习方程的基础。
知识与技能:
过程与方法:
情感态度与
价值观:
教学目标
结合具体情境,体会用字母表示数的意义,学会用字母表示数、数量关系和计算公式,体会字母表示数的意义,形成初步的符号感。
使学生完整地经历用含有字母的式子表示简单的数量、数量关系和计算公式探索规律的过程,培养学生分析、归纳、概括的能力。
培养学生用字母表示数的意识和兴趣,使学生进一步产生对数学学习的好奇心。
教学重点
教学难点
让学生经历和体验用字母表示数的抽象过程,理解用字母表示数的意义,会用字母表示数和简单的数量关系。
从具体问题情境抽象概括出用字母表示数和数量关系,掌握含有字母的乘法算式的简写方法。
创设学习氛围
激发学习欲望
增强学习兴趣
角色扮演法
小组合作法
情境设置法
说教法
创设问题情境
培养问题意识
促进思维发展
组织探究活动
提高实践能力
培养创新精神
合作交流法
自主探究法
动手操作
回顾总结
说学法
归纳小结
巩固新知
——教学过程——
探索新知
创设情境
一、创设情境
一首永远唱不完的儿歌
1只青蛙,1张嘴,2只眼睛,4条腿,
扑通一声跳下水 2只青蛙,2张嘴,4只眼睛,8条腿,
扑通扑通跳下水
3只青蛙,3张嘴,6只眼睛,12条
腿, 扑通扑通扑通跳下水
…
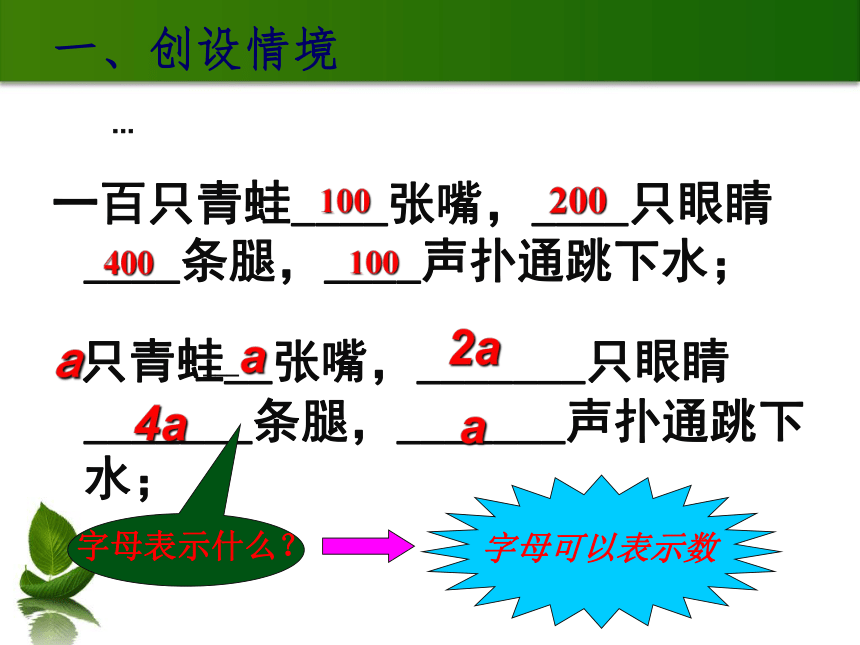
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
a只青蛙__张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
___a
2a
4a
a
100
200
400
100
字母表示什么?
字母可以表示数
一、创设情境
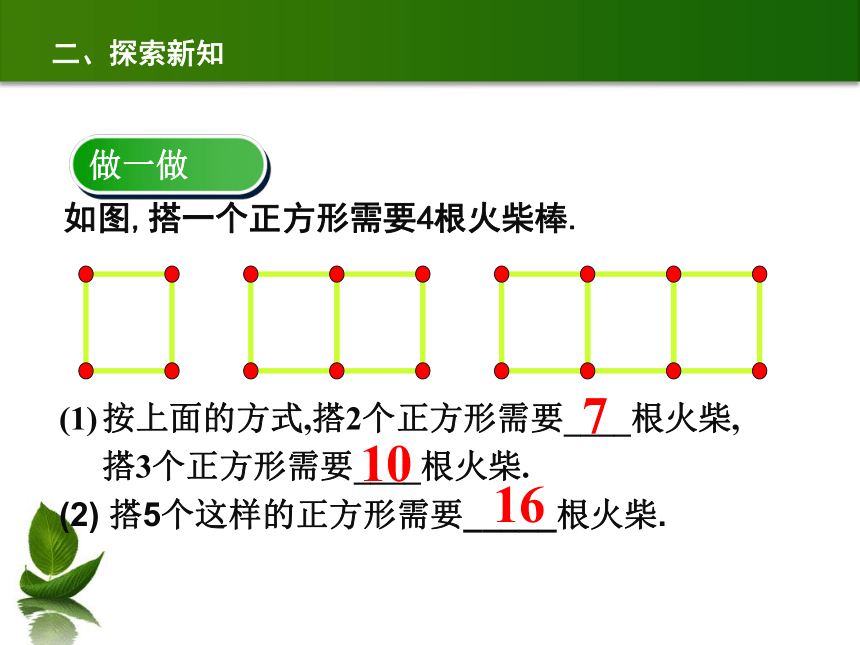
如图,搭一个正方形需要4根火柴棒.
二、探索新知
按上面的方式,搭2个正方形需要____根火柴, 搭3个正方形需要____根火柴.
(2) 搭5个这样的正方形需要_____根火柴.
7
10
16
做一做
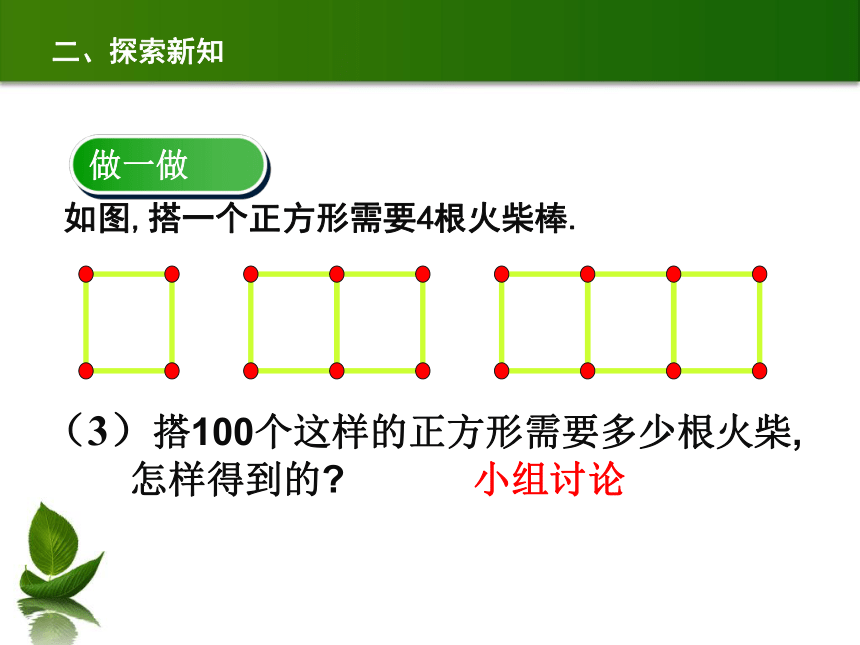
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
(3)搭100个这样的正方形需要多少根火柴,
怎样得到的 小组讨论
第1个
4根
第2个
第100个
3根
3根
…
二、探索新知
…
先摆 1根
第1个
3根
第100个
3根
二、探索新知
…
第1个
2根
第2个
2根
第100个
2根
二、探索新知
第1个
4根
第100个
4根
…
二、探索新知
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
(4) 如果用a表示所搭正方形的个数, 那么搭a个
这样的正方形需要多少根火柴
…
第1个
4根
第2个
第100个
3根
3根
二、探索新知
问:如果用a表示所搭正方形的个数,那么搭a个这样的正方形需要多少火柴棒?
4+3(a-1)
a+a+(a+1)
1+3a
4a -(a -1)
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
根据你的计算方法,搭200个这样的正方形需要______根火柴棒; 搭1000个这样的正方形需要_______根火柴棒;
601
3001
三、巩固新知
你能举出一些字母表示数和数量关系的例子吗
想一想
用字母表示数的运算律
a + b = b + a
(a + b) +c= a +(b + c)
a·b = b·a
(a + b) c = ac+bc
加法结合律
加法交换律
乘法交换律
乘法结合律
乘法分配律
(ab)c = a(bc)
注意:
用字母表示
乘法时,乘号
可以用“·”表示
或者省略
不写
巩固新知
a
a
a
b
a
h
a
h
a
h
b
S = a2
S = ab
S = ah
S =
S = ah
三、巩固新知
除法通常写成分数的形
式,如1÷a通常写成
姐姐比弟弟大4岁
弟弟的岁数 姐姐的岁数
1 1+4
2 2+4
…… ……
a
a+4
b
b+4
利用字母表示数,能把数和数量关系一般化地、简明地表示出来。
用字母表示数
(1)温度由t℃下降2℃后是 ℃。
(2)今年李华m岁,去年李华 岁,5年后李华 岁。
(3)a个人n天完成一项工作,那么平均每人每天的工作量为 。
……
(t-2)
(m-1)
(m+5)
4+3(a-1)
a+a+(a+1)
1+3a
4a -(a-1)
a表示什么数?
若搭建200个正方形,你能用简单巧妙的方法快速准确的求得所需根数吗?
答:4+3(200-1)=601根
小结
用字母表示数的意义:有助于揭示概念的本质特征,能使数量之间的关系更加简明,更具有普遍意义。使思维过程简约化,易于形成概念系统。
字母可以表示任意的数,也可以表示特定意义的公式,还可以表示符合条件的某一个数,甚至可以表示具有某些规律的数,总之字母可以简明的将数量关系表示出来。
我们把这些含有字母的式子叫做代数式。
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
表示运算律
意义
字母表示数含字母的式子
表示探索出来的规律
表示计算公式
三角形面积计算公式等
1.若老师的年龄看作x岁,老师比你大y岁,那么你的年龄是多少呢?
(x-y)岁
6.含有字母的式子的书写规则
2.练习簿的单价为a元,买50本练习簿的总价为多少元
50×a元=50a元
3.练习簿单价为a元,买b本总价为_____元。
5.买3本练习簿为a元,则练习簿的单价为___元。
ab
1.5b
3
2
b
或
a
3
字母与字母相乘时,乘号可以省略
4.练习簿的单价为 元,买b本总价为___元。
1
2
1
6.练习簿的单价为a元,买1本练习簿的总价为多少元
a元
当和式中出现字母,且后面带有单位时,要将式子用括号括起来
数与字母相乘时,数字写在字母前面
带分数与字母相乘时, 带分数要写成假分数
字母与字母相除时,除号用分数线代替
-1或1与字母相乘时,1可以省略。
例1.判断下列各式的写法是否正确.
2.数与数相乘时,乘号不能省略
3.数与数相加时,加号不能省略
4.字母与字母相乘时,乘号可以省略
1.数与字母相乘时,数字写在字母前面
6. -1或1与字母相乘时,1可以省略。
7.带分数与字母相乘时,带分数要化成
假分数的形式。
5.字母与字母相除时,除号用分数线代替
(1)a×0.8写作a0.8
(2)5×6写作56
(3)a+2写作2a
(4)a×b写作ab
(5)a÷b写作
(6)-1×a写作-a
(7)2 ×a写作 a
( )
( )
( )
( )
( )
( )
( )
√
√
√
√
×
×
×
例2.一个两位数,把个位上的数与十位上的数对调,请你判断
新的两位数与原来的两位数的差有什么特点,并说明道理。
分析:
假设这个数是47,那么对调后的新数是74,根据题意得
74-47=27
假设这个数是68,那么对调后的新数是86,根据题意得
86-68=18
……
观察27,18……这些数都是9的倍数。
是不是所有的情况都是这样的呢?我们可以用字母表示
数来解答这个问题。
解:设这个数十位上的数是a,个位上的数是b,那么这个数是
10a+b,根据题意对调后的新数是10b+a,所以:
(10b+a)-(10a+b)=9b-9a=9(b-a),由此可知新的两位数
与原来的两位数的差是9的倍数。
练一练
1、明明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是明明的3倍, 则亮亮的速度可以表示为_______米/秒.
2、如图, 用字母表示图中
阴影部分的面积是_________
随堂练习
m
n
p
q
练一练
1、明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是明明的3倍, 则亮亮的速度可以表示为_______米/秒.
2、如图, 用字母表示图中
阴影部分的面积是_________
随堂练习
m
n
p
q
3v
mn-pq
1、五年计划期间植树造林,如果每年植树 公顷荒山,那么这五年内植树荒山 公顷。
2、如果小红用t小时走完的路程为s千米,那么她走这段路的平均速度为 千米/时。
3、如图,某广场四角上铺了四分之一
的圆形草地,若圆形的半径为r米,则
共有草地 平分米。
4、三角形的三边长为3a、4b、5c,
其周长为 。
巩固练习
5
πr2
3a+4b+5c
1、字母可以表示任何数。
2、可用字母表示运算律、计算公式以及一些简单问题中的数量关系和变化规律。
3、用字母表示的书写注意事项:
(1)乘号可以用 “·”表示或者省略不写,数字写在字母前面,如:a×b通常写成a·b或ab;3a
(2)除法通常写成分数,如1÷a通常写成
(3)同个字母在不同的问题中可以代表不同的量;在同个问题中,不同的量要用不同的字母表示。
五、课堂总结
§3.1 字母表示数
教材分析
教学过程
板书设计
——说 课 环 节——
教法学法
教材分析
所处的地位与作用:
本节课是在学生掌握了常见的数量关系、周长、面积计算等知识的基础上安排的,这些都是理解本单元所学知识的重要基础。本课内容看似浅显、平淡,但它是由具体的数和运算符号组成的式子过渡到含有字母的式子,使学生建立初步的符号感,是学生学习数学的一个转折点,也是认识过程上的一次飞跃。对提高学生的数学认知水平有着非常重要的作用。同时本单元知识又是学生进入代数知识学习的入门知识,是学习方程的基础。
知识与技能:
过程与方法:
情感态度与
价值观:
教学目标
结合具体情境,体会用字母表示数的意义,学会用字母表示数、数量关系和计算公式,体会字母表示数的意义,形成初步的符号感。
使学生完整地经历用含有字母的式子表示简单的数量、数量关系和计算公式探索规律的过程,培养学生分析、归纳、概括的能力。
培养学生用字母表示数的意识和兴趣,使学生进一步产生对数学学习的好奇心。
教学重点
教学难点
让学生经历和体验用字母表示数的抽象过程,理解用字母表示数的意义,会用字母表示数和简单的数量关系。
从具体问题情境抽象概括出用字母表示数和数量关系,掌握含有字母的乘法算式的简写方法。
创设学习氛围
激发学习欲望
增强学习兴趣
角色扮演法
小组合作法
情境设置法
说教法
创设问题情境
培养问题意识
促进思维发展
组织探究活动
提高实践能力
培养创新精神
合作交流法
自主探究法
动手操作
回顾总结
说学法
归纳小结
巩固新知
——教学过程——
探索新知
创设情境
一、创设情境
一首永远唱不完的儿歌
1只青蛙,1张嘴,2只眼睛,4条腿,
扑通一声跳下水 2只青蛙,2张嘴,4只眼睛,8条腿,
扑通扑通跳下水
3只青蛙,3张嘴,6只眼睛,12条
腿, 扑通扑通扑通跳下水
…
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
a只青蛙__张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
___a
2a
4a
a
100
200
400
100
字母表示什么?
字母可以表示数
一、创设情境
如图,搭一个正方形需要4根火柴棒.
二、探索新知
按上面的方式,搭2个正方形需要____根火柴, 搭3个正方形需要____根火柴.
(2) 搭5个这样的正方形需要_____根火柴.
7
10
16
做一做
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
(3)搭100个这样的正方形需要多少根火柴,
怎样得到的 小组讨论
第1个
4根
第2个
第100个
3根
3根
…
二、探索新知
…
先摆 1根
第1个
3根
第100个
3根
二、探索新知
…
第1个
2根
第2个
2根
第100个
2根
二、探索新知
第1个
4根
第100个
4根
…
二、探索新知
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
(4) 如果用a表示所搭正方形的个数, 那么搭a个
这样的正方形需要多少根火柴
…
第1个
4根
第2个
第100个
3根
3根
二、探索新知
问:如果用a表示所搭正方形的个数,那么搭a个这样的正方形需要多少火柴棒?
4+3(a-1)
a+a+(a+1)
1+3a
4a -(a -1)
如图,搭一个正方形需要4根火柴棒.
二、探索新知
做一做
根据你的计算方法,搭200个这样的正方形需要______根火柴棒; 搭1000个这样的正方形需要_______根火柴棒;
601
3001
三、巩固新知
你能举出一些字母表示数和数量关系的例子吗
想一想
用字母表示数的运算律
a + b = b + a
(a + b) +c= a +(b + c)
a·b = b·a
(a + b) c = ac+bc
加法结合律
加法交换律
乘法交换律
乘法结合律
乘法分配律
(ab)c = a(bc)
注意:
用字母表示
乘法时,乘号
可以用“·”表示
或者省略
不写
巩固新知
a
a
a
b
a
h
a
h
a
h
b
S = a2
S = ab
S = ah
S =
S = ah
三、巩固新知
除法通常写成分数的形
式,如1÷a通常写成
姐姐比弟弟大4岁
弟弟的岁数 姐姐的岁数
1 1+4
2 2+4
…… ……
a
a+4
b
b+4
利用字母表示数,能把数和数量关系一般化地、简明地表示出来。
用字母表示数
(1)温度由t℃下降2℃后是 ℃。
(2)今年李华m岁,去年李华 岁,5年后李华 岁。
(3)a个人n天完成一项工作,那么平均每人每天的工作量为 。
……
(t-2)
(m-1)
(m+5)
4+3(a-1)
a+a+(a+1)
1+3a
4a -(a-1)
a表示什么数?
若搭建200个正方形,你能用简单巧妙的方法快速准确的求得所需根数吗?
答:4+3(200-1)=601根
小结
用字母表示数的意义:有助于揭示概念的本质特征,能使数量之间的关系更加简明,更具有普遍意义。使思维过程简约化,易于形成概念系统。
字母可以表示任意的数,也可以表示特定意义的公式,还可以表示符合条件的某一个数,甚至可以表示具有某些规律的数,总之字母可以简明的将数量关系表示出来。
我们把这些含有字母的式子叫做代数式。
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
表示运算律
意义
字母表示数含字母的式子
表示探索出来的规律
表示计算公式
三角形面积计算公式等
1.若老师的年龄看作x岁,老师比你大y岁,那么你的年龄是多少呢?
(x-y)岁
6.含有字母的式子的书写规则
2.练习簿的单价为a元,买50本练习簿的总价为多少元
50×a元=50a元
3.练习簿单价为a元,买b本总价为_____元。
5.买3本练习簿为a元,则练习簿的单价为___元。
ab
1.5b
3
2
b
或
a
3
字母与字母相乘时,乘号可以省略
4.练习簿的单价为 元,买b本总价为___元。
1
2
1
6.练习簿的单价为a元,买1本练习簿的总价为多少元
a元
当和式中出现字母,且后面带有单位时,要将式子用括号括起来
数与字母相乘时,数字写在字母前面
带分数与字母相乘时, 带分数要写成假分数
字母与字母相除时,除号用分数线代替
-1或1与字母相乘时,1可以省略。
例1.判断下列各式的写法是否正确.
2.数与数相乘时,乘号不能省略
3.数与数相加时,加号不能省略
4.字母与字母相乘时,乘号可以省略
1.数与字母相乘时,数字写在字母前面
6. -1或1与字母相乘时,1可以省略。
7.带分数与字母相乘时,带分数要化成
假分数的形式。
5.字母与字母相除时,除号用分数线代替
(1)a×0.8写作a0.8
(2)5×6写作56
(3)a+2写作2a
(4)a×b写作ab
(5)a÷b写作
(6)-1×a写作-a
(7)2 ×a写作 a
( )
( )
( )
( )
( )
( )
( )
√
√
√
√
×
×
×
例2.一个两位数,把个位上的数与十位上的数对调,请你判断
新的两位数与原来的两位数的差有什么特点,并说明道理。
分析:
假设这个数是47,那么对调后的新数是74,根据题意得
74-47=27
假设这个数是68,那么对调后的新数是86,根据题意得
86-68=18
……
观察27,18……这些数都是9的倍数。
是不是所有的情况都是这样的呢?我们可以用字母表示
数来解答这个问题。
解:设这个数十位上的数是a,个位上的数是b,那么这个数是
10a+b,根据题意对调后的新数是10b+a,所以:
(10b+a)-(10a+b)=9b-9a=9(b-a),由此可知新的两位数
与原来的两位数的差是9的倍数。
练一练
1、明明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是明明的3倍, 则亮亮的速度可以表示为_______米/秒.
2、如图, 用字母表示图中
阴影部分的面积是_________
随堂练习
m
n
p
q
练一练
1、明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是明明的3倍, 则亮亮的速度可以表示为_______米/秒.
2、如图, 用字母表示图中
阴影部分的面积是_________
随堂练习
m
n
p
q
3v
mn-pq
1、五年计划期间植树造林,如果每年植树 公顷荒山,那么这五年内植树荒山 公顷。
2、如果小红用t小时走完的路程为s千米,那么她走这段路的平均速度为 千米/时。
3、如图,某广场四角上铺了四分之一
的圆形草地,若圆形的半径为r米,则
共有草地 平分米。
4、三角形的三边长为3a、4b、5c,
其周长为 。
巩固练习
5
πr2
3a+4b+5c
1、字母可以表示任何数。
2、可用字母表示运算律、计算公式以及一些简单问题中的数量关系和变化规律。
3、用字母表示的书写注意事项:
(1)乘号可以用 “·”表示或者省略不写,数字写在字母前面,如:a×b通常写成a·b或ab;3a
(2)除法通常写成分数,如1÷a通常写成
(3)同个字母在不同的问题中可以代表不同的量;在同个问题中,不同的量要用不同的字母表示。
五、课堂总结
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
