江苏省某中学2023-2024学年高一上学期12月测试数学试卷(无答案)
文档属性
| 名称 | 江苏省某中学2023-2024学年高一上学期12月测试数学试卷(无答案) | 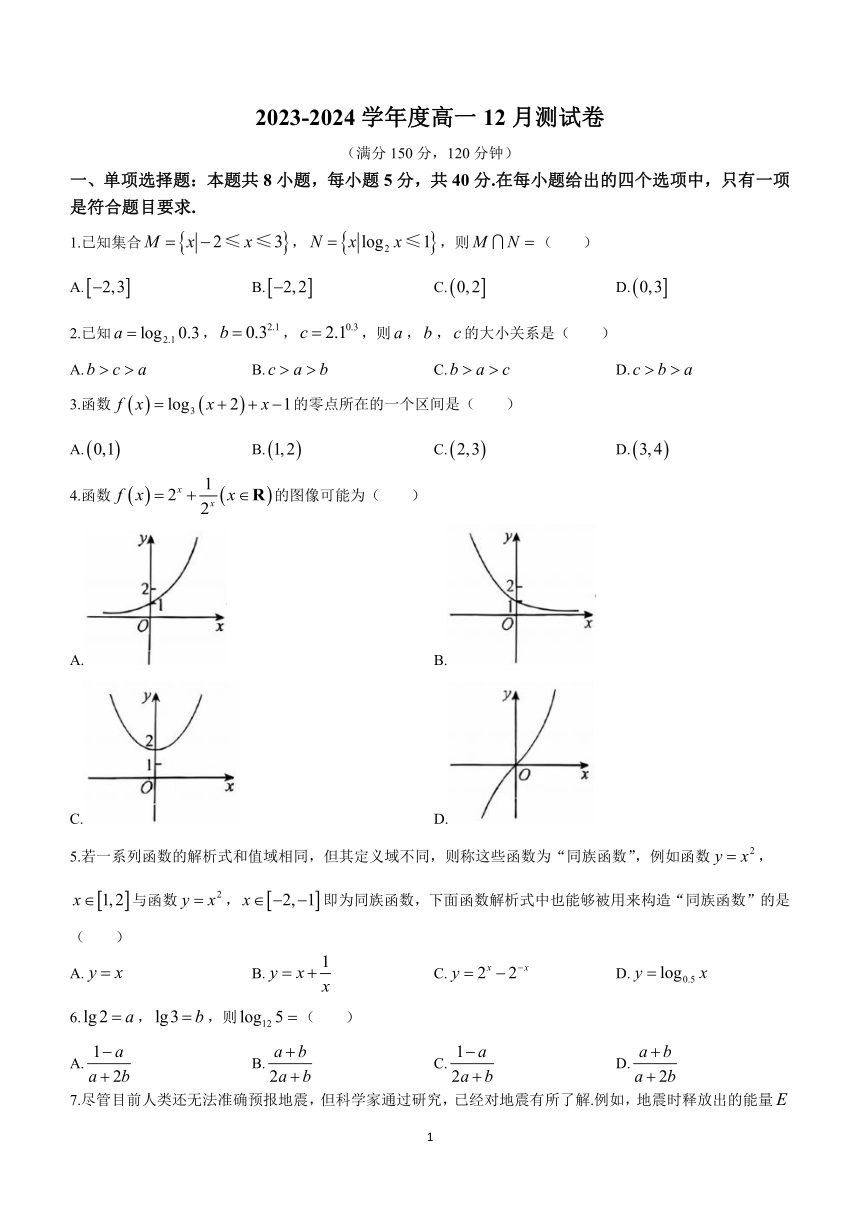 | |
| 格式 | doc | ||
| 文件大小 | 436.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-16 22:52:16 | ||
图片预览


文档简介
2023-2024学年度高一12月测试卷
(满分150分,120分钟)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
1.已知集合,,则( )
A. B. C. D.
2.已知,,,则,,的大小关系是( )
A. B. C. D.
3.函数的零点所在的一个区间是( )
A. B. C. D.
4.函数的图像可能为( )
A. B.
C. D.
5.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数,与函数,即为同族函数,下面函数解析式中也能够被用来构造“同族函数”的是( )
A. B. C. D.
6.,,则( )
A. B. C. D.
7.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解.例如,地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为,2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2013年4月20日在四川省雅安市芦山县发生7.0级地震级地震的( )倍.
A. B.3 C. D.
8.已知函数,若(其中),则的最小值为( ).
A. B. C.2 D.4
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数,,则下列选项中正确的有( )
A.为奇函数 B.为偶函数
C.的值域为 D.有最小值0
10.如图,某河塘浮萍面积()与时间(月)的关系式为,则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第4个月时,浮萍面积会超过
C.浮萍面积蔓延到只需6个月
D.若浮萍面积蔓延到,,所需时间分别为,,,则
11.已知函数若互不相等的实数,,满足,则的值可以是( )
A. B. C. D.
12.给出以下四个结论,其中所有正确结论的序号是( )
A.若函数的定义域为,则函数的定义域是
B.函数(其中,且)的图象过定点
C.当时,幂函数的图象是一条直线
D.若,则的取值范围是
三、填空:本题共4小题,每小题5分,共20分.
13.关于的不等式的解集为____________.
14.若幂函数在区间上是减函数,则整数_________.
15.著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为,空气温度为,则分钟后物体的温度(单位:℃)满足:.若当空气温度为30℃时,某物体的温度从90℃下降到60℃用时14分钟.则再经过28分钟后,该物体的温度为_________℃.
16.已知是方程的一个根,是的一个根,则_______.
四、解答题:本小题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知,.
(1)分别求和;
(2)若,且,求.
18.已知正实数满足不等式.
(1)解关于的不等式.
(2)若函数在区间上有最大值,求实数的值.
19.已知.
(1)求函数的定义域;
(2)求证:为偶函数;
(3)指出方程的实数根个数,并说明理由.
20.科技创新在经济发展中的作用日益凸显.某科技公司为实现9000万元的投资收益目标,准备制定激励研发人员的奖励方案:当投资收益达到3000万元时,按投资收益进行奖励,要求奖金(单位:万元)随投资收益(单位:万元)的增加而增加,奖金总数不低于100万元,且奖金总数不超过投资收益的20%.
(1)现有三个奖励函数模型:①,②,③,.试分析这三个函数模型是否符合公司要求?
(2)根据(1)中符合公司要求的函数模型,要使奖金额达到350万元,公司的投资收益至少要达到多少万元?
21.已知函数,.
(1)利用函数单调性的定义,证明:函数在区间上是减函数;
(2)若存在实数,(),使得函数在区间上的值域为,求实数的取值范围.
22.已知函数,.
(1)求的值;
(2)若方程在区间上有唯一的实数解,求实数的取值范围;
(3)对任意,若关于的不等式在上恒成立,求实数的取值范围.
(满分150分,120分钟)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求.
1.已知集合,,则( )
A. B. C. D.
2.已知,,,则,,的大小关系是( )
A. B. C. D.
3.函数的零点所在的一个区间是( )
A. B. C. D.
4.函数的图像可能为( )
A. B.
C. D.
5.若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数,与函数,即为同族函数,下面函数解析式中也能够被用来构造“同族函数”的是( )
A. B. C. D.
6.,,则( )
A. B. C. D.
7.尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解.例如,地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为,2011年3月11日,日本东北部海域发生里氏9.0级地震,它所释放出来的能量是2013年4月20日在四川省雅安市芦山县发生7.0级地震级地震的( )倍.
A. B.3 C. D.
8.已知函数,若(其中),则的最小值为( ).
A. B. C.2 D.4
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知函数,,则下列选项中正确的有( )
A.为奇函数 B.为偶函数
C.的值域为 D.有最小值0
10.如图,某河塘浮萍面积()与时间(月)的关系式为,则下列说法正确的是( )
A.浮萍每月增加的面积都相等
B.第4个月时,浮萍面积会超过
C.浮萍面积蔓延到只需6个月
D.若浮萍面积蔓延到,,所需时间分别为,,,则
11.已知函数若互不相等的实数,,满足,则的值可以是( )
A. B. C. D.
12.给出以下四个结论,其中所有正确结论的序号是( )
A.若函数的定义域为,则函数的定义域是
B.函数(其中,且)的图象过定点
C.当时,幂函数的图象是一条直线
D.若,则的取值范围是
三、填空:本题共4小题,每小题5分,共20分.
13.关于的不等式的解集为____________.
14.若幂函数在区间上是减函数,则整数_________.
15.著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为,空气温度为,则分钟后物体的温度(单位:℃)满足:.若当空气温度为30℃时,某物体的温度从90℃下降到60℃用时14分钟.则再经过28分钟后,该物体的温度为_________℃.
16.已知是方程的一个根,是的一个根,则_______.
四、解答题:本小题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知,.
(1)分别求和;
(2)若,且,求.
18.已知正实数满足不等式.
(1)解关于的不等式.
(2)若函数在区间上有最大值,求实数的值.
19.已知.
(1)求函数的定义域;
(2)求证:为偶函数;
(3)指出方程的实数根个数,并说明理由.
20.科技创新在经济发展中的作用日益凸显.某科技公司为实现9000万元的投资收益目标,准备制定激励研发人员的奖励方案:当投资收益达到3000万元时,按投资收益进行奖励,要求奖金(单位:万元)随投资收益(单位:万元)的增加而增加,奖金总数不低于100万元,且奖金总数不超过投资收益的20%.
(1)现有三个奖励函数模型:①,②,③,.试分析这三个函数模型是否符合公司要求?
(2)根据(1)中符合公司要求的函数模型,要使奖金额达到350万元,公司的投资收益至少要达到多少万元?
21.已知函数,.
(1)利用函数单调性的定义,证明:函数在区间上是减函数;
(2)若存在实数,(),使得函数在区间上的值域为,求实数的取值范围.
22.已知函数,.
(1)求的值;
(2)若方程在区间上有唯一的实数解,求实数的取值范围;
(3)对任意,若关于的不等式在上恒成立,求实数的取值范围.
同课章节目录
