6.4 用一次函数解决问题 同步练习(无答案) 苏科版数学八年级上册
文档属性
| 名称 | 6.4 用一次函数解决问题 同步练习(无答案) 苏科版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 238.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览


文档简介
2023-2024学年苏科版数学八年级上册
6.4用一次函数解决问题
(行程+销售+分段收费问题)
【典型例题】
题型一:用一次函数解决行程问题
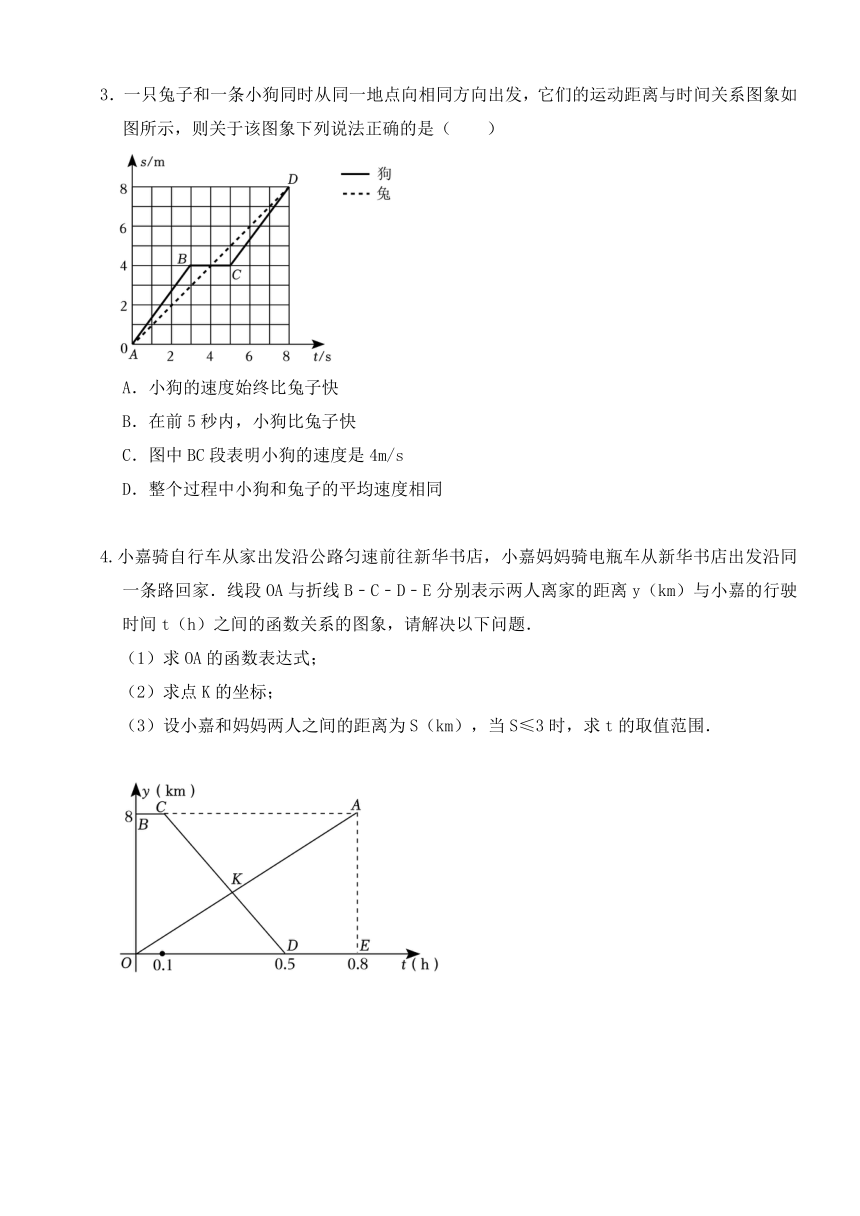
1.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,甲无人机的飞行速度为 m/s.
2.在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a、b的值分别为( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
3.一只兔子和一条小狗同时从同一地点向相同方向出发,它们的运动距离与时间关系图象如图所示,则关于该图象下列说法正确的是( )
A.小狗的速度始终比兔子快
B.在前5秒内,小狗比兔子快
C.图中BC段表明小狗的速度是4m/s
D.整个过程中小狗和兔子的平均速度相同
4.小嘉骑自行车从家出发沿公路匀速前往新华书店,小嘉妈妈骑电瓶车从新华书店出发沿同一条路回家.线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(km)与小嘉的行驶时间t(h)之间的函数关系的图象,请解决以下问题.
(1)求OA的函数表达式;
(2)求点K的坐标;
(3)设小嘉和妈妈两人之间的距离为S(km),当S≤3时,求t的取值范围.
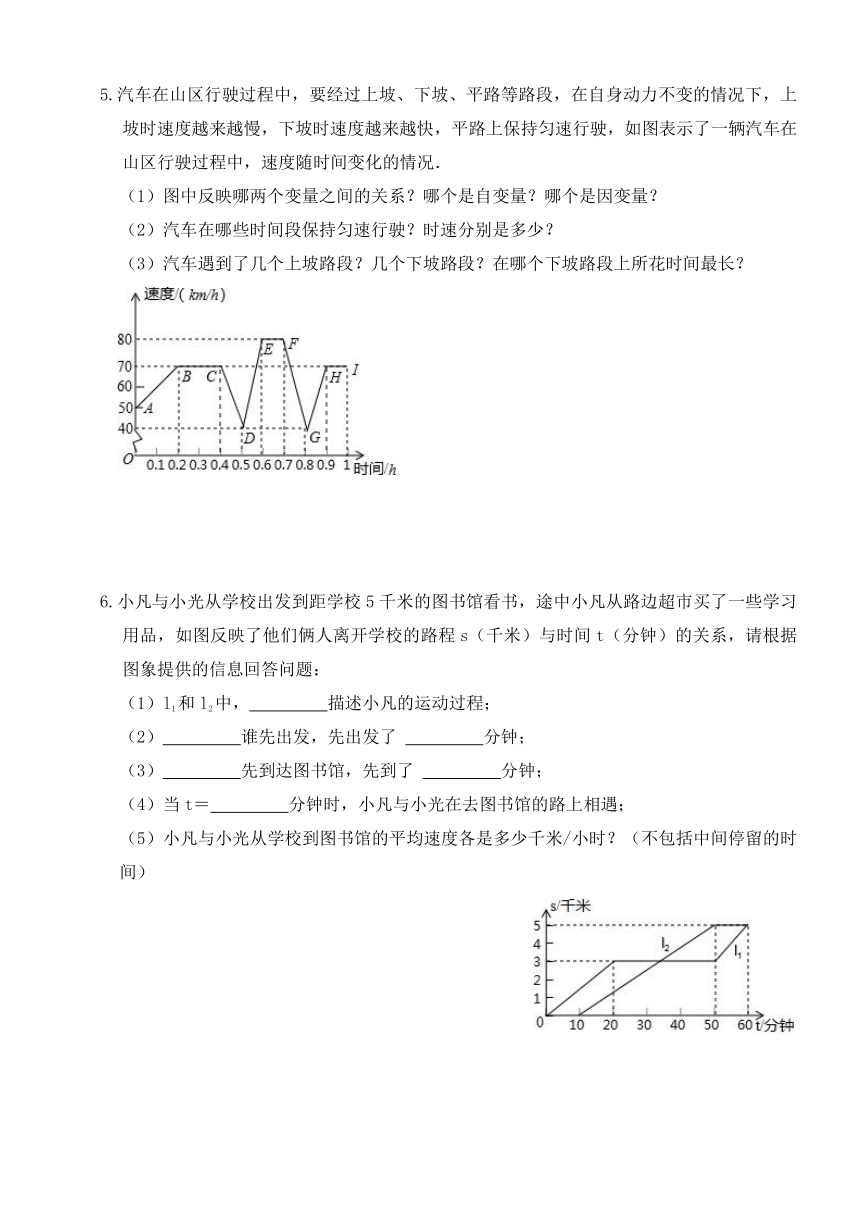
5.汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.
(1)图中反映哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?
6.小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反映了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1)l1和l2中, 描述小凡的运动过程;
(2) 谁先出发,先出发了 分钟;
(3) 先到达图书馆,先到了 分钟;
(4)当t= 分钟时,小凡与小光在去图书馆的路上相遇;
(5)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)
题型二:用一次函数解决销售问题
1.如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是____.
①第24天的销售量为200件;②第10天销售一件产品的利润是15元;③第12天与第30天这两天的日销售利润相等;④第30天的日销售利润是750元.
2.如图是本地区一种产品30天的销售图象,图①是产品日销售量(单位:件)与时间(单位:天)的函数关系,图②是一件产品的销售利润(单位:元)与时间(单位:天)的函数关系,第27天的日销售利润是__________元.
3.李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:
品名 甲蔬菜 乙蔬菜
批发价/(元/kg) 4.8 4
零售价/(元/kg) 7.21 5.6
(1)若他批发甲、乙两种蔬菜共40kg花180元,求批发甲、乙两种蔬菜各多少千克?(列方程或方程组求解)
(2)若他批发甲、乙两种蔬菜共80kg花m元,设批发甲种蔬菜nkg,求m与n的函数关系式;
(3)在(2)的条件下,全部卖完蔬菜后要保证利润不低于176元,至少批发甲种蔬菜多少千克?
4.6月13日是“文化和自然遗产日”,某商店为了抓住此次活动的商机,决定购买一些纪念品进行销售,若购进A种纪念品20件,B种纪念品10件,需要2000元;若购进A种纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若每件A种纪念品的售价为60元,每件B种纪念品的售价为180元.考虑到市场需求,商店决定购进这两种纪念品共300件,要求购进B种纪念品的数量不少于30件,设购进B种纪念品m件,总利润为w元,请写出总利润w(元)与m(件)的函数关系式,并根据函数关系式说明利润最高时的进货方案.
5.某工厂生产A、B两种产品共1000件,其中A产品个数不少于B产品个数,生产总成本不超过18000元,已知两种产品的单个成本和零售价如下表,设该工厂生产A产品x件.
产品 成本(元/个) 零售价(元/个).
A 20 25
B 10 12
(1)该厂把这1000件产品以零售价全部售出,求该厂能获得的最大利润:
(2)受疫情影响,A产品的成本比原来增加m(m>0)元/个;该厂在不调整零售价情况下,将1000件产品全部出售获得的最低利润是3000元,求m的值.
6.某厂计划生产,两种产品若干件,已知两种产品的成本价和销售价如表:
类别 种产品 种产品
成本价元件
销售价元件
(1)第一次工厂用元资金生产了,两种产品共件,求两种产品各生产多少件?
(2)第二次工厂生产时,工厂规定种产品生产数量不得超过种产品生产数量的一半.工厂计划生产两种产品共件,应如何设计生产方案才能获得最大利润,最大利润是多少?
题型三:用一次函数解决分段收费问题
1.出租车的收费标准为:5km以内(含5km)起步价为8元,超过5km后每1km收1.5元,如果用表示出租车行驶的路程,表示的是出租车应收的车费,请你表示y与s之间的表达式___________.
2.某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定的质量,则需购买行李票,行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带的行李质量是( )千克.
A.60 B.50 C.40 D.30
3.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨2.5元收费.如果超过20吨,未超过的部分按每吨2.5元收.超过的部分按每吨3.3元收费.
(1)若该城市某户6月份用水18吨,该户6月份水费是多少?
(2)设某户某月用水量为x吨(x>20),应缴水费为y元,写出y关于x的函数关系式.
(3)某用户8月份水费为83元,求该用户8月份用水量.
4.为改善生态环境,某市开展植树造林活动,现甲、乙两家林场有相同的树苗可供选择,具体销售方案如下:甲林场每株树苗都是1.8元,乙林场树苗售价:当购买树苗的数量不超过1000棵时,每棵2元;当超过1000棵时,超过1000棵的部分,每棵1.6元.设购买树苗x棵,到两家林场购买所需费用分别为y甲、y乙元.
(1)如果需要购买1500棵树苗,若都在甲林场购买,所需费用为 元,若都在乙林场购买,所需费用为 元;
(2)直接写出y甲、y乙与x之间的函数关系式;
(3)求当购买树苗超过1000棵时,选择哪个林场合算,为什么?
5.某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)
x(人) … 2500 2750 3000 3500 4000 …
y(元) … -1000 -500 0 1000 2000 …
(1)根据函数的定义,y是关于x的函数吗?
(2)结合表格解答下列问题:
①公交车票的单价是多少元?
②当x=2750时,y的值是多少?它的实际意义是什么?
6.某市为了节约用水,采用分段收费标准.设居民每月应交水费y(元),用水量x(立方米).
用水量x(立方米) 应交水费y(元)
不超过12立方米 每立方米3元
超过12立方米 超过的部分每立方米4元
(1)若某户居民某月用水10立方米,应交水费 元;若用水15立方米,应交水费 元.
(2)当用水量超过12立方米时,求每月应交水费y(元)与用水量x(立方米)之间的函数关系式;
(3)若某户居民某月交水费41元,则该户居民用水多少立方米?
6.4用一次函数解决问题
(行程+销售+分段收费问题)
【典型例题】
题型一:用一次函数解决行程问题
1.甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示,甲无人机的飞行速度为 m/s.
2.在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a、b的值分别为( )
A.39,26 B.39,26.4 C.38,26 D.38,26.4
3.一只兔子和一条小狗同时从同一地点向相同方向出发,它们的运动距离与时间关系图象如图所示,则关于该图象下列说法正确的是( )
A.小狗的速度始终比兔子快
B.在前5秒内,小狗比兔子快
C.图中BC段表明小狗的速度是4m/s
D.整个过程中小狗和兔子的平均速度相同
4.小嘉骑自行车从家出发沿公路匀速前往新华书店,小嘉妈妈骑电瓶车从新华书店出发沿同一条路回家.线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(km)与小嘉的行驶时间t(h)之间的函数关系的图象,请解决以下问题.
(1)求OA的函数表达式;
(2)求点K的坐标;
(3)设小嘉和妈妈两人之间的距离为S(km),当S≤3时,求t的取值范围.
5.汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.
(1)图中反映哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(3)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?
6.小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反映了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1)l1和l2中, 描述小凡的运动过程;
(2) 谁先出发,先出发了 分钟;
(3) 先到达图书馆,先到了 分钟;
(4)当t= 分钟时,小凡与小光在去图书馆的路上相遇;
(5)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)
题型二:用一次函数解决销售问题
1.如图是本地区一种产品30天的销售图象,图1是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图2是一件产品的销售利润z(单位,元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列正确结论的序号是____.
①第24天的销售量为200件;②第10天销售一件产品的利润是15元;③第12天与第30天这两天的日销售利润相等;④第30天的日销售利润是750元.
2.如图是本地区一种产品30天的销售图象,图①是产品日销售量(单位:件)与时间(单位:天)的函数关系,图②是一件产品的销售利润(单位:元)与时间(单位:天)的函数关系,第27天的日销售利润是__________元.
3.李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:
品名 甲蔬菜 乙蔬菜
批发价/(元/kg) 4.8 4
零售价/(元/kg) 7.21 5.6
(1)若他批发甲、乙两种蔬菜共40kg花180元,求批发甲、乙两种蔬菜各多少千克?(列方程或方程组求解)
(2)若他批发甲、乙两种蔬菜共80kg花m元,设批发甲种蔬菜nkg,求m与n的函数关系式;
(3)在(2)的条件下,全部卖完蔬菜后要保证利润不低于176元,至少批发甲种蔬菜多少千克?
4.6月13日是“文化和自然遗产日”,某商店为了抓住此次活动的商机,决定购买一些纪念品进行销售,若购进A种纪念品20件,B种纪念品10件,需要2000元;若购进A种纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若每件A种纪念品的售价为60元,每件B种纪念品的售价为180元.考虑到市场需求,商店决定购进这两种纪念品共300件,要求购进B种纪念品的数量不少于30件,设购进B种纪念品m件,总利润为w元,请写出总利润w(元)与m(件)的函数关系式,并根据函数关系式说明利润最高时的进货方案.
5.某工厂生产A、B两种产品共1000件,其中A产品个数不少于B产品个数,生产总成本不超过18000元,已知两种产品的单个成本和零售价如下表,设该工厂生产A产品x件.
产品 成本(元/个) 零售价(元/个).
A 20 25
B 10 12
(1)该厂把这1000件产品以零售价全部售出,求该厂能获得的最大利润:
(2)受疫情影响,A产品的成本比原来增加m(m>0)元/个;该厂在不调整零售价情况下,将1000件产品全部出售获得的最低利润是3000元,求m的值.
6.某厂计划生产,两种产品若干件,已知两种产品的成本价和销售价如表:
类别 种产品 种产品
成本价元件
销售价元件
(1)第一次工厂用元资金生产了,两种产品共件,求两种产品各生产多少件?
(2)第二次工厂生产时,工厂规定种产品生产数量不得超过种产品生产数量的一半.工厂计划生产两种产品共件,应如何设计生产方案才能获得最大利润,最大利润是多少?
题型三:用一次函数解决分段收费问题
1.出租车的收费标准为:5km以内(含5km)起步价为8元,超过5km后每1km收1.5元,如果用表示出租车行驶的路程,表示的是出租车应收的车费,请你表示y与s之间的表达式___________.
2.某长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定的质量,则需购买行李票,行李费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.旅客最多可免费携带的行李质量是( )千克.
A.60 B.50 C.40 D.30
3.某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨2.5元收费.如果超过20吨,未超过的部分按每吨2.5元收.超过的部分按每吨3.3元收费.
(1)若该城市某户6月份用水18吨,该户6月份水费是多少?
(2)设某户某月用水量为x吨(x>20),应缴水费为y元,写出y关于x的函数关系式.
(3)某用户8月份水费为83元,求该用户8月份用水量.
4.为改善生态环境,某市开展植树造林活动,现甲、乙两家林场有相同的树苗可供选择,具体销售方案如下:甲林场每株树苗都是1.8元,乙林场树苗售价:当购买树苗的数量不超过1000棵时,每棵2元;当超过1000棵时,超过1000棵的部分,每棵1.6元.设购买树苗x棵,到两家林场购买所需费用分别为y甲、y乙元.
(1)如果需要购买1500棵树苗,若都在甲林场购买,所需费用为 元,若都在乙林场购买,所需费用为 元;
(2)直接写出y甲、y乙与x之间的函数关系式;
(3)求当购买树苗超过1000棵时,选择哪个林场合算,为什么?
5.某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)
x(人) … 2500 2750 3000 3500 4000 …
y(元) … -1000 -500 0 1000 2000 …
(1)根据函数的定义,y是关于x的函数吗?
(2)结合表格解答下列问题:
①公交车票的单价是多少元?
②当x=2750时,y的值是多少?它的实际意义是什么?
6.某市为了节约用水,采用分段收费标准.设居民每月应交水费y(元),用水量x(立方米).
用水量x(立方米) 应交水费y(元)
不超过12立方米 每立方米3元
超过12立方米 超过的部分每立方米4元
(1)若某户居民某月用水10立方米,应交水费 元;若用水15立方米,应交水费 元.
(2)当用水量超过12立方米时,求每月应交水费y(元)与用水量x(立方米)之间的函数关系式;
(3)若某户居民某月交水费41元,则该户居民用水多少立方米?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
