推理与证明

课件20张PPT。复习:合情推理归纳推理 从特殊到一般
类比推理 从特殊到特殊从具体问题出发观察、分析
比较、联想提出猜想归纳
类比小明是一名高二年级的学生，17岁，迷恋上网络，沉迷于虚拟的世界当中。由于每月的零花钱不够用，便向亲戚要钱，但这仍然满足不了需求，于是就产生了歹念，强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元，这应该不会很严重吧？？？
如果你是法官，你会如何判决呢？小明到底是不是犯罪呢？情景创设：生活中的例子法官判决的过程是合情推理吗？ 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 铜能够导电.铜是金属, (2100+1)不能被2整除.(2100+1)是奇数, tan 周期函数 tan 三角函数,是合情推理吗？你还能举出其他一些例子吗？演绎推理从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理．注：１．演绎推理是由一般到特殊的推理；２．“三段论”是演绎推理的一般模式
⑴大前提--- 已知的一般原理；
⑵小前提--- 所研究的特殊情况；
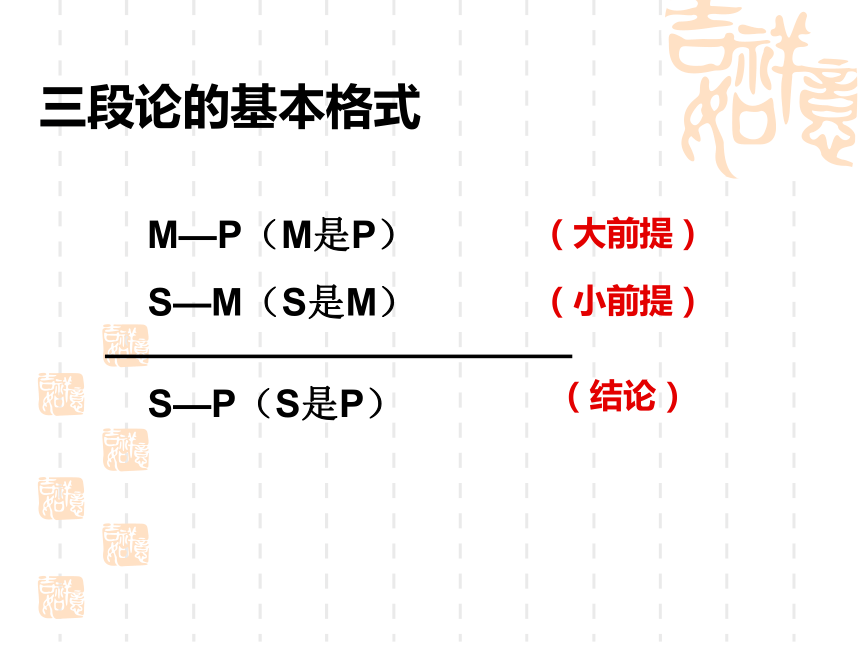
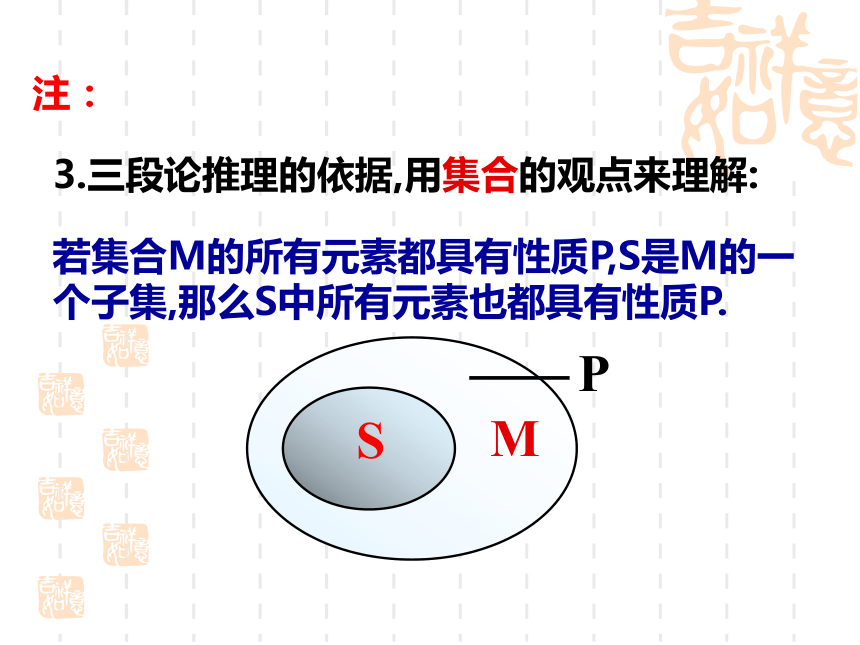
⑶结论----- 据一般原理，对特殊情况做出的判断． 演绎推理三段论的基本格式M—P（M是P）S—M（S是M）S—P（S是P）（大前提）（小前提）（结论）3.三段论推理的依据,用集合的观点来理解:若集合M的所有元素都具有性质P,S是M的一个子集,那么S中所有元素也都具有性质P.注：大前提：刑法规定抢劫罪是以非法占有为目的，使用暴力、胁迫或其他方法，强行劫取公私财物的行为。其刑事责任年龄起点为14周岁，对财物的数额没有要求。小前提：小明超过14周岁，强行向路人抢取钱财50元。结论：小明犯了抢劫罪。小明是一名高二年级的学生，17岁，迷恋上网络，沉迷于虚拟的世界当中。由于每月的零花钱不够用，便向亲戚要钱，但这仍然满足不了需求，于是就产生了歹念，强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元，这应该不会很严重吧？？ 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 所以，铜能够导电.铜是金属, 所以，(2100+1)不能被2整除.(2100+1)是奇数,所以 tan 周期函数 tan 三角函数, 演绎推理解：二次函数的图象是一条抛物线 （大前提）例2.已知lg2=m,计算lg0.8解 （1） lgan=nlga(a>0)lg8=lg23lg8=3lg2 lg(a/b)=lga-lgb(a>0,b>0)lg0.8=lg(8/10)lg0.8=lg8-lg10=3lg2-1例3.如图;在锐角三角形ABC中,AD⊥BC, BE⊥AC,
D,E是垂足,求证AB的中点M到D,E的距离相等. (1)因为有一个内角是只直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=900所以△ABD是直角三角形同理△ABE是直角三角形(2)因为直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线所以 DM= AB同理 EM= AB所以 DM = EM大前提小前提结论大前提小前提结论证明:例4：已知a,b,m均为正实数，b0,所以mb0,(大前提）(小前提）(大前提）(小前提）(大前提）(小前提）(结论）(结论）(结论） 演绎推理（练习）练习1：把下列推理恢复成完全的三段论: 演绎推理（练习）练习2. 指出下列推理中的错误,并分析产生错误的原因;(1)整数是自然数,-3是整数,-3是自然数;(2)无理数是无限小数,是无限小数,是无理数.大前提 错误练习3:证明函数f(x)=-x2+2x在(-∞,1]上是增函数.满足对于任意x1,x2∈D,若x1f(x1)-f(x2)=(-x12+2x1)-(x22+2x2)
=(x2-x1)(x1+x2-2) 因为x10
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1) ②类比是由特殊到特殊的推理;
③演绎推理是由一般到特殊的
推理.
2 从推理的结论来看：
合情推理的结论不一定正确,有待证明;
演绎推理得到的结论一定正确.2 数学结论、证明思路的发现,主要靠合情推理.1 演绎推理是证明数学结论、建立数学体系的重要思维过程.合情推理与演绎推理的相关说明：