2.3 平行线的性质(第2课时)同步课件(共28张PPT)
文档属性
| 名称 | 2.3 平行线的性质(第2课时)同步课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览





文档简介
(共28张PPT)
2.3 平行线的性质
第2课时
学习目标
1)熟练应用平行线的性质与判定条件解决问题。
2)通过证明过程,初步理解简单的几何推理。
重点
熟练应用平行线的性质与判定条件解决问题。
难点
通过证明过程,初步理解简单的几何推理。
平行线的性质 平行线的判定
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
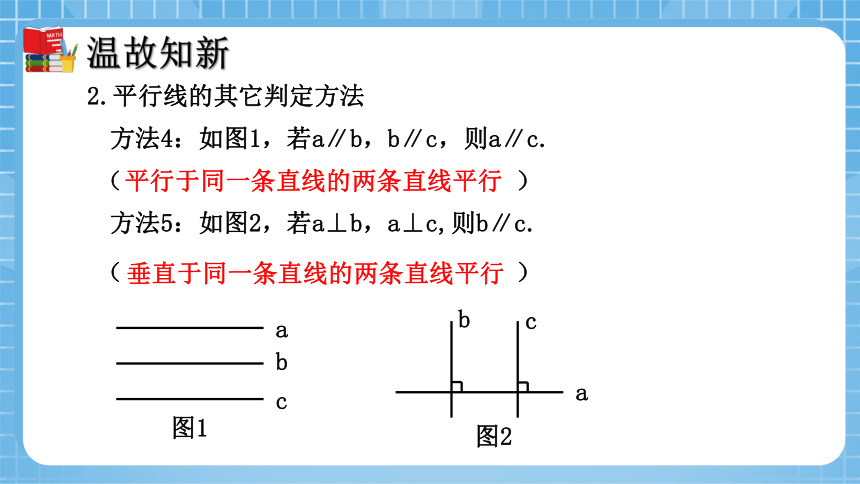
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
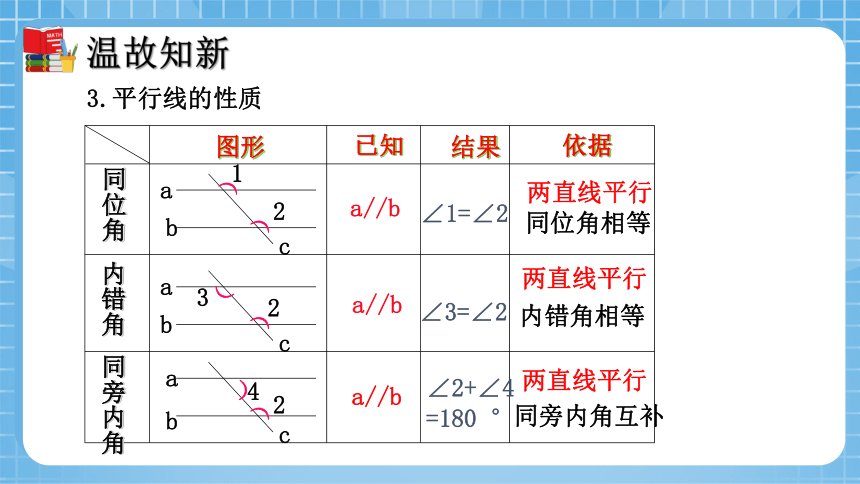
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
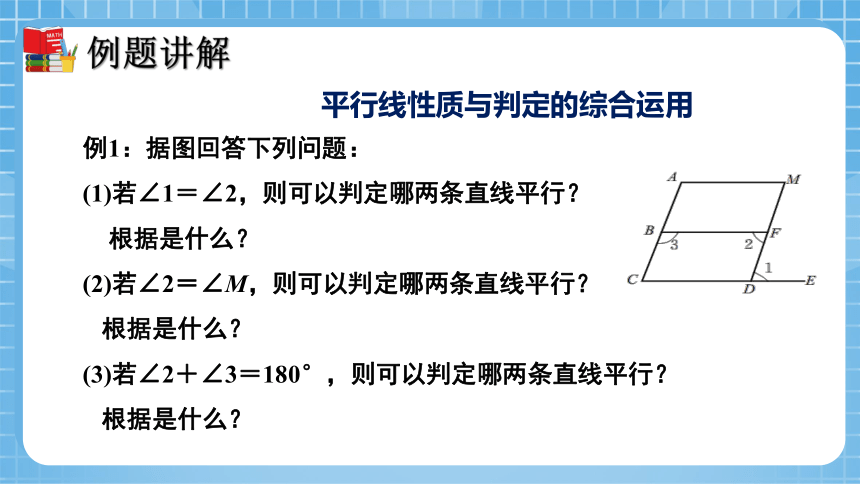
平行线性质与判定的综合运用
例1:据图回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?
根据是什么?
(2)若∠2=∠M,则可以判定哪两条直线平行?
根据是什么?
(3)若∠2+∠3=180°,则可以判定哪两条直线平行?
根据是什么?
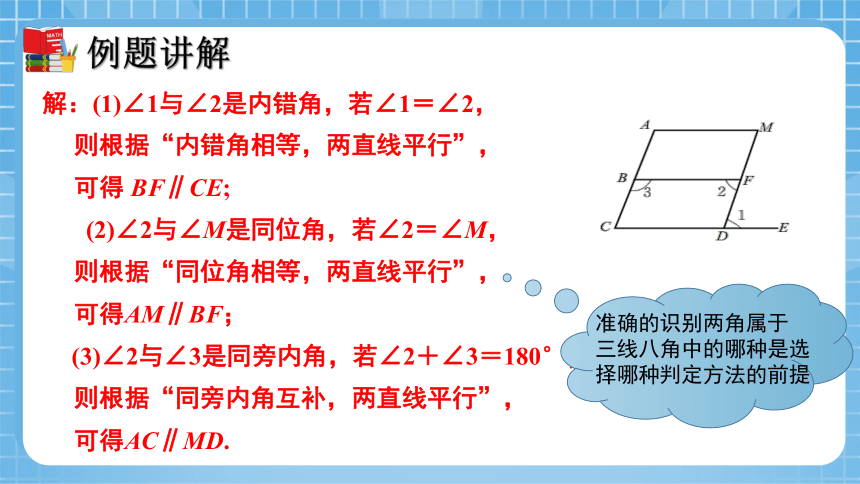
解:(1)∠1与∠2是内错角,若∠1=∠2,
则根据“内错角相等,两直线平行”,
可得 BF∥CE;
(2)∠2与∠M是同位角,若∠2=∠M,
则根据“同位角相等,两直线平行”,
可得AM∥BF;
(3)∠2与∠3是同旁内角,若∠2+∠3=180°,
则根据“同旁内角互补,两直线平行”,
可得AC∥MD.
准确的识别两角属于
三线八角中的哪种是选择哪种判定方法的前提
例2.如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
解:因为∠1= ∠2,
根据“内错角相等,两直线平行” ,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
例3.如图,已知直线 a∥b,直线 c∥d,∠1=107°,求∠2,∠3 的度数.
2
1
3
a
b
c
d
解:因为a∥b,
根据“两直线平行,内错角相等”,
所以 ∠2 = ∠1 = 107° .
因为 c∥d,
根据“两直线平行,同旁内角互补”,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3=180°-∠1=180°-107°= 73° .
判定条件
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
判定是已知角的关系得平行关系,性质是已知平行关系得角的关系。两者的条件和结论刚好相反,也就是说平行线的判定与性质是互逆的。
如下图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,你能求出另外两个角的度数吗?
解: ∵AD//BC ,∠A=115°
∴∠A+∠B=180 °
(两直线平行,同旁内角互补)
∴∠B=65° ∠C=70°
两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?
m
n
l
3
4
2
1
1.平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2.判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
例4.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B. 85°
C. 95°
D. 100°
B
1.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35°
B.70°
C.90°
D.110°
D
2.如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°
3. 一小区大门的栏杆如图,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
A. 180° B. 270° C. 300° D. 360°
B
4.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠2=∠4
5.如图,射线平分,且.求证:AB‖CD.
【详解】证明:∵平分(已知)
∴∠2=∠ABC(角平分线的定义)
∵∠1=∠BCE(对顶角相等)
又∵∠l+∠2=180°(已知)
∴∠BCE+∠ABC=180°(等量代换)
∴ AB‖CD (同旁内角互补,两直线平行)
6.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β-∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
7. 如图,已知∠A=∠1,∠C=∠F.求证:BC∥EF.
证明:∵∠A=∠1(已知)
∴AC∥DF(同位角相等,两直线平行)
∴∠C=∠BGD(两直线平行,同位角相等)
又∵∠C=∠F(已知)
∴∠BGD=∠F(等量代换)
∴BC∥EF(同位角相等,两直线平行)
8.如图,在四边形ABCD中,延长AD至E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.(1)求证:AB∥CD;(2)求∠2的度数.
【详解】(1)证明:∵AC平分∠DAB,
∴∠BAC=∠DAC=∠DAB=×70°=35°,
又∵∠1=35°,∴∠1=∠BAC,∴AB∥CD;
(2)∵AB∥CD,∴∠2=∠DAB=70°.
9. 如图,已知AD∥BC,∠1=∠2,试说明:∠3+∠4=180°.
解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3(等量代换).
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
10.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
【详解】(1)∵∠CED=∠GHD,∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,∴∠C=∠FGD,
又∵∠C=∠EFG,∴∠FGD=∠EFG,
∴AB∥CD,∴∠AED+∠D=180°;
11.林湾乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村,水渠从C村沿什么方向修建,可以保持与AB的方向一致?
解:由题可得∠1=65°
当EC保持与AB的方向一致,则EC∥BD可得:
∠NCE=∠CBD=25°+65°=90°
故∠2=65°
即从C村沿北偏东65°方向建设,可保持与AB的方向一致.
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
4 两直线平行, 同位角相等.
5 两直线平行, 内错角相等.
6 两直线平行, 同旁内角互补.
习题2.6
第1、2、3题
2.3 平行线的性质
第2课时
学习目标
1)熟练应用平行线的性质与判定条件解决问题。
2)通过证明过程,初步理解简单的几何推理。
重点
熟练应用平行线的性质与判定条件解决问题。
难点
通过证明过程,初步理解简单的几何推理。
平行线的性质 平行线的判定
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
平行线性质与判定的综合运用
例1:据图回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?
根据是什么?
(2)若∠2=∠M,则可以判定哪两条直线平行?
根据是什么?
(3)若∠2+∠3=180°,则可以判定哪两条直线平行?
根据是什么?
解:(1)∠1与∠2是内错角,若∠1=∠2,
则根据“内错角相等,两直线平行”,
可得 BF∥CE;
(2)∠2与∠M是同位角,若∠2=∠M,
则根据“同位角相等,两直线平行”,
可得AM∥BF;
(3)∠2与∠3是同旁内角,若∠2+∠3=180°,
则根据“同旁内角互补,两直线平行”,
可得AC∥MD.
准确的识别两角属于
三线八角中的哪种是选择哪种判定方法的前提
例2.如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
解:因为∠1= ∠2,
根据“内错角相等,两直线平行” ,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
例3.如图,已知直线 a∥b,直线 c∥d,∠1=107°,求∠2,∠3 的度数.
2
1
3
a
b
c
d
解:因为a∥b,
根据“两直线平行,内错角相等”,
所以 ∠2 = ∠1 = 107° .
因为 c∥d,
根据“两直线平行,同旁内角互补”,
所以 ∠1 + ∠3 = 180° ,
所以 ∠3=180°-∠1=180°-107°= 73° .
判定条件
性质
同位角相等
内错角相等
同旁内角互补
两直线平行
判定是已知角的关系得平行关系,性质是已知平行关系得角的关系。两者的条件和结论刚好相反,也就是说平行线的判定与性质是互逆的。
如下图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,你能求出另外两个角的度数吗?
解: ∵AD//BC ,∠A=115°
∴∠A+∠B=180 °
(两直线平行,同旁内角互补)
∴∠B=65° ∠C=70°
两条直线被第三条直线所截,如果同位角相等,那么内错角相等吗?同旁内角互补吗?
m
n
l
3
4
2
1
1.平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2.判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
例4.如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B. 85°
C. 95°
D. 100°
B
1.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
A.35°
B.70°
C.90°
D.110°
D
2.如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
A.35°
B.40°
C.45°
D.50°
3. 一小区大门的栏杆如图,当栏杆抬起时,BA垂直于地面AE,CD平行于地面AE,则∠ABC+∠BCD的度数为( )
A. 180° B. 270° C. 300° D. 360°
B
4.如图,若∠A+∠ABC=180°,则下列结论正确的是( )
A.∠1=∠2
B.∠2=∠3
C.∠1=∠3
D.∠2=∠4
5.如图,射线平分,且.求证:AB‖CD.
【详解】证明:∵平分(已知)
∴∠2=∠ABC(角平分线的定义)
∵∠1=∠BCE(对顶角相等)
又∵∠l+∠2=180°(已知)
∴∠BCE+∠ABC=180°(等量代换)
∴ AB‖CD (同旁内角互补,两直线平行)
6.如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A.∠α+∠β=180°
B.∠β-∠α=90°
C.∠β=3∠α
D.∠α+∠β=90°
7. 如图,已知∠A=∠1,∠C=∠F.求证:BC∥EF.
证明:∵∠A=∠1(已知)
∴AC∥DF(同位角相等,两直线平行)
∴∠C=∠BGD(两直线平行,同位角相等)
又∵∠C=∠F(已知)
∴∠BGD=∠F(等量代换)
∴BC∥EF(同位角相等,两直线平行)
8.如图,在四边形ABCD中,延长AD至E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.(1)求证:AB∥CD;(2)求∠2的度数.
【详解】(1)证明:∵AC平分∠DAB,
∴∠BAC=∠DAC=∠DAB=×70°=35°,
又∵∠1=35°,∴∠1=∠BAC,∴AB∥CD;
(2)∵AB∥CD,∴∠2=∠DAB=70°.
9. 如图,已知AD∥BC,∠1=∠2,试说明:∠3+∠4=180°.
解:因为AD∥BC(已知),
所以∠1=∠3(两直线平行,内错角相等).
因为∠1=∠2(已知),
所以∠2=∠3(等量代换).
所以BE∥DF(同位角相等,两直线平行).
所以∠3+∠4=180°(两直线平行,同旁内角互补).
10.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
【详解】(1)∵∠CED=∠GHD,∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,∴∠C=∠FGD,
又∵∠C=∠EFG,∴∠FGD=∠EFG,
∴AB∥CD,∴∠AED+∠D=180°;
11.林湾乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村,水渠从C村沿什么方向修建,可以保持与AB的方向一致?
解:由题可得∠1=65°
当EC保持与AB的方向一致,则EC∥BD可得:
∠NCE=∠CBD=25°+65°=90°
故∠2=65°
即从C村沿北偏东65°方向建设,可保持与AB的方向一致.
1 同位角相等,两直线平行.
2 内错角相等,两直线平行.
3 同旁内角互补,两直线平行.
4 两直线平行, 同位角相等.
5 两直线平行, 内错角相等.
6 两直线平行, 同旁内角互补.
习题2.6
第1、2、3题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
