人教版七年级数学上册第三章《一元一次方程》单元练习题 (1)(含答案)
文档属性
| 名称 | 人教版七年级数学上册第三章《一元一次方程》单元练习题 (1)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 30.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 19:45:55 | ||
图片预览


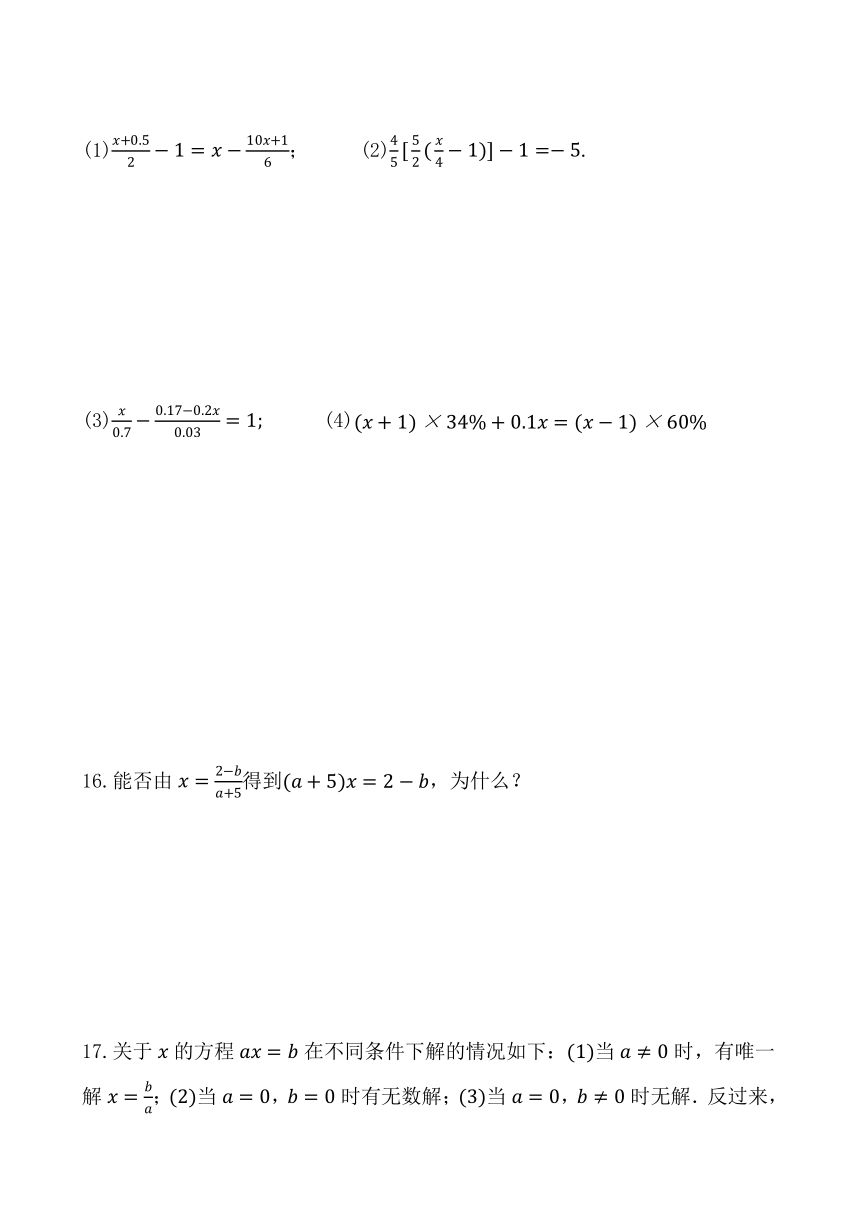

文档简介
人教版七年级数学上册第三章《一元一次方程》单元练习题
学校:______姓名:______班级:______
一、单选题
1.代数式与的差是,则的值是( )
A. B. C. D.
2.若等式可以变形为,则有()
A. B. C.≠ D.为任意有理数
3.若关于的一元一次方程的解是,则的值是( )
A. B. C. D.
4.小明在解方程时,不小心将方程中的一个常数污损了,被污损的方程是.怎么办呢?小明想了想,便翻看书后的答案,得知此方程的解为,于是他很快补出了这个常数,你能补出这个常数吗?它应是( )
A. B. C. D.
5.将方程去分母后,得( )
A. B.
C. D.
6.一架飞机在两城间飞行,顺风航行要小时,逆风航行要小时,风速为千米时,设飞机无风时的速度为每小时千米,则下列方程正确是( )
A.()() B.
C.()() D.
二、填空题
7.已知,则当 时,.
8.若代数式与代数式的和为,则
9.已知,则 .
10.现在父亲的年龄是儿子年龄的5倍,6年后父亲年龄是儿子年龄的3倍,则现在父亲的年龄是 岁,儿子的年龄是 岁.
11.已知是方程的解,则的值为 .
12.朵朵幼儿园的阿姨给小朋友分饼干,如果每人分个还少个;如果每人分个又多个,则朵朵幼儿园共有多少个小朋友?若设幼儿园共有个小朋友,则可列方程 .
13.图是由一些偶数排成的数阵,按照图所示方式圈出个数,这样的个数之间具有一定的关系,按照同样的方式,如果圈出的个数和(如图),则最中间的数的值是 .
14.我国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去里外的某关口,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.若设此人第六天走的路程为里,则可列方程为 .
三、解答题
15.解方程:
(1); (2).
(3) (4)
16.能否由得到,为什么?
17.关于的方程在不同条件下解的情况如下:当时,有唯一解;当,时有无数解;当,时无解.反过来,若关于的方程有唯一解,则;若这个方程有无数解,则,;若这个方程无解,则,.
(1)若,则关于的方程的解的情况是 (填“有唯一解”“有无数解”或“无解”).
(2)已知关于的方程无解,求的值.
(3)当时,解关于的方程,并求出当取哪些整数时,该方程的解也是整数.
18.某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件元的价格购进了某品牌衬衫件,并以每件元的价格销售了件,商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,当每件衬衫降价多少元时,销售完这批衬衫正好达到盈利的预期目标.
19.周大爷准备去银行存一笔现金.经过咨询,银行一年定期储蓄的年利率为,两年定期储蓄的年利率为.如果将这笔现金存入两年定期储蓄,期满后将比先存一年定期储蓄到期后连本带息再转存一年定期的方式多得利息元.周大爷准备存的这笔现金是多少元?
20.有一列火车要以每分钟的速度过两座铁桥,过第二座铁桥比过第一座铁桥多时间,又知第二座铁桥的长度比第一座铁桥长度的倍短,试求两座铁桥的长分别为多少(火车长度忽略不计).
21.在开展校园足球对抗赛中,规定每队胜一场得分,平一场得分,负一场得分,我校女子足球队一共比赛了场,且保持了不败战绩,一共得了分,我校女子足球队胜了多少场?平了多少场?
22.某出租汽车站已停有辆出租汽车,第一辆出租汽车出发后每隔分钟就有一辆出租汽车开出,在第一辆汽车开出分钟后,有一辆出租汽车进站,以后每隔分钟就有一辆出租汽车回站,回站的出租汽车在原有的出租汽车依次开出后又依次每隔分钟开出一辆,问:第一辆出租汽车开出后,经过最少多长时间,车站不能正点发车?
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
7.
8.
9.或
10.30 ;6
11.
12.
13.
14.
15.(1)解:.去分母,得.去括号,得.移项、合并同类项,得系数化为得.
(2)去中括号,得.去小括号,得.去分母,得.移项、合并同类项,得.
(3)原方程可化为.去分母,得.去括号,得.移项、合并同类项,得.系数化为,得.
(4)去百分号,得.
方程两边同除以得 .
去括号,得.
移项、合并同类项,得.
系数化为得.
16.解:能.理由:因为由已知条件可知,
所以等式两边都乘,得.
17.(1)有唯一解
(2)去分母,得.去括号,得.移项、合并同类项,得.因为此方程无解,所以.所以.
(3)移项、合并同类项,得.因为≠,所以.当和都是整数,可得的值可以为,,,.则的值可以为,,,.
18.解:设每件衬衫降价元.
依题意,有 ,
解得.
答:当每件衬衫降价元时,销售完这批衬衫正好达到盈利的预期目标.
19.解:设周大爷准备存的这笔现金是元.
由题意,得.
解得.
答:周大爷准备存的这笔现金是元.
20.解:设第一座铁桥的长为,则第二座铁桥的长为,
过第一座铁桥所需要的时间为,过第二座铁桥所需要的时间为.
根据题意,得,
解得.
所以
答:第一座铁桥长,第二座铁桥长.
21.解:设我校女子足球队胜了场,则平了()场,
(),
解得,
则平了(场),
答:我校女子足球队胜了场,平了场
22.设回车数是辆,则发车数是辆,
依题意得,
,
,
答:经过分钟后车站不能正点发车.
学校:______姓名:______班级:______
一、单选题
1.代数式与的差是,则的值是( )
A. B. C. D.
2.若等式可以变形为,则有()
A. B. C.≠ D.为任意有理数
3.若关于的一元一次方程的解是,则的值是( )
A. B. C. D.
4.小明在解方程时,不小心将方程中的一个常数污损了,被污损的方程是.怎么办呢?小明想了想,便翻看书后的答案,得知此方程的解为,于是他很快补出了这个常数,你能补出这个常数吗?它应是( )
A. B. C. D.
5.将方程去分母后,得( )
A. B.
C. D.
6.一架飞机在两城间飞行,顺风航行要小时,逆风航行要小时,风速为千米时,设飞机无风时的速度为每小时千米,则下列方程正确是( )
A.()() B.
C.()() D.
二、填空题
7.已知,则当 时,.
8.若代数式与代数式的和为,则
9.已知,则 .
10.现在父亲的年龄是儿子年龄的5倍,6年后父亲年龄是儿子年龄的3倍,则现在父亲的年龄是 岁,儿子的年龄是 岁.
11.已知是方程的解,则的值为 .
12.朵朵幼儿园的阿姨给小朋友分饼干,如果每人分个还少个;如果每人分个又多个,则朵朵幼儿园共有多少个小朋友?若设幼儿园共有个小朋友,则可列方程 .
13.图是由一些偶数排成的数阵,按照图所示方式圈出个数,这样的个数之间具有一定的关系,按照同样的方式,如果圈出的个数和(如图),则最中间的数的值是 .
14.我国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是:有人要去里外的某关口,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.若设此人第六天走的路程为里,则可列方程为 .
三、解答题
15.解方程:
(1); (2).
(3) (4)
16.能否由得到,为什么?
17.关于的方程在不同条件下解的情况如下:当时,有唯一解;当,时有无数解;当,时无解.反过来,若关于的方程有唯一解,则;若这个方程有无数解,则,;若这个方程无解,则,.
(1)若,则关于的方程的解的情况是 (填“有唯一解”“有无数解”或“无解”).
(2)已知关于的方程无解,求的值.
(3)当时,解关于的方程,并求出当取哪些整数时,该方程的解也是整数.
18.某校七年级社会实践小组去商场调查商品销售情况,了解到该商场以每件元的价格购进了某品牌衬衫件,并以每件元的价格销售了件,商场准备采取促销措施,将剩下的衬衫降价销售.请你帮商场计算一下,当每件衬衫降价多少元时,销售完这批衬衫正好达到盈利的预期目标.
19.周大爷准备去银行存一笔现金.经过咨询,银行一年定期储蓄的年利率为,两年定期储蓄的年利率为.如果将这笔现金存入两年定期储蓄,期满后将比先存一年定期储蓄到期后连本带息再转存一年定期的方式多得利息元.周大爷准备存的这笔现金是多少元?
20.有一列火车要以每分钟的速度过两座铁桥,过第二座铁桥比过第一座铁桥多时间,又知第二座铁桥的长度比第一座铁桥长度的倍短,试求两座铁桥的长分别为多少(火车长度忽略不计).
21.在开展校园足球对抗赛中,规定每队胜一场得分,平一场得分,负一场得分,我校女子足球队一共比赛了场,且保持了不败战绩,一共得了分,我校女子足球队胜了多少场?平了多少场?
22.某出租汽车站已停有辆出租汽车,第一辆出租汽车出发后每隔分钟就有一辆出租汽车开出,在第一辆汽车开出分钟后,有一辆出租汽车进站,以后每隔分钟就有一辆出租汽车回站,回站的出租汽车在原有的出租汽车依次开出后又依次每隔分钟开出一辆,问:第一辆出租汽车开出后,经过最少多长时间,车站不能正点发车?
参考答案
1.A
2.C
3.B
4.C
5.D
6.C
7.
8.
9.或
10.30 ;6
11.
12.
13.
14.
15.(1)解:.去分母,得.去括号,得.移项、合并同类项,得系数化为得.
(2)去中括号,得.去小括号,得.去分母,得.移项、合并同类项,得.
(3)原方程可化为.去分母,得.去括号,得.移项、合并同类项,得.系数化为,得.
(4)去百分号,得.
方程两边同除以得 .
去括号,得.
移项、合并同类项,得.
系数化为得.
16.解:能.理由:因为由已知条件可知,
所以等式两边都乘,得.
17.(1)有唯一解
(2)去分母,得.去括号,得.移项、合并同类项,得.因为此方程无解,所以.所以.
(3)移项、合并同类项,得.因为≠,所以.当和都是整数,可得的值可以为,,,.则的值可以为,,,.
18.解:设每件衬衫降价元.
依题意,有 ,
解得.
答:当每件衬衫降价元时,销售完这批衬衫正好达到盈利的预期目标.
19.解:设周大爷准备存的这笔现金是元.
由题意,得.
解得.
答:周大爷准备存的这笔现金是元.
20.解:设第一座铁桥的长为,则第二座铁桥的长为,
过第一座铁桥所需要的时间为,过第二座铁桥所需要的时间为.
根据题意,得,
解得.
所以
答:第一座铁桥长,第二座铁桥长.
21.解:设我校女子足球队胜了场,则平了()场,
(),
解得,
则平了(场),
答:我校女子足球队胜了场,平了场
22.设回车数是辆,则发车数是辆,
依题意得,
,
,
答:经过分钟后车站不能正点发车.
